Triangle With Squares!

Geometry Level 4

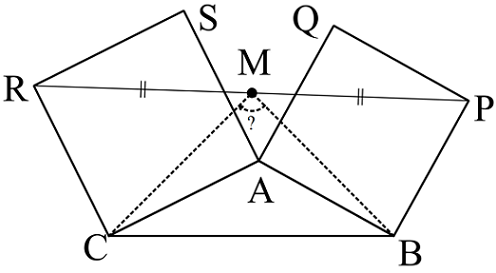
Given a triangle $ABC$ , construct two squares $ABPQ$ and $ACRS$ . Suppose that $M$ is the midpoint of $PR$ . Join $MB$ and $MC$ . Find $\angle BMC$ .

Details and Assumptions :

$P$ and $C$ are on opposite side of $AB$ .
$R$ and $B$ are on opposite side of $AC$ .

If you're interested, here is follow up question .

The answer is 90.

1 solution

Ahmad Saad
Apr 30, 2016

Relevant wiki: Similar Triangles - Problem Solving - Medium

Figure above shows a parallelogram $AKMJ$ with
$\angle RKM = \angle PJM = \angle RAP = \angle PAR = 90^\circ = \angle BAC$ .
$\angle CKM = \angle BJM = \angle PAR - 90^\circ = \angle BAC$ ,
$KM = AJ = JB$ , $KC = KA = JM$ .

Then the two triangles $KMC$ and $JBM$ are congruent, so $\angle KMC = \angle JBM, \angle JMB = \angle KCM$ ,
therefore, $\angle KMC + \angle JMB = 180^\circ -\angle BAC$ .

$\angle JMK = \angle PAR = 90^\circ + \angle BAC\Rightarrow \angle BMC = 360^\circ - ( \angle JMK + \angle JMB + \angle KMC ) = \boxed{90^\circ}$ .

An easy way is using complex numbers. Choose A as the origin and B & C as z1 and z2 respectively. For your figure, R is z1(1+i) and P is z2(1-i).

Kumar Saurav - 5 years, 1 month ago

Exactly how I did it!

A Former Brilliant Member - 5 years, 1 month ago

Hi Deeparaj.Could you just have a look at my note named "Doubt in a combinatorics problem"?

Indraneel Mukhopadhyaya - 5 years, 1 month ago

@Indraneel Mukhopadhyaya – Sure. But, I'm kinda weak in combi...

A Former Brilliant Member - 5 years, 1 month ago

I think you have to prove AKMJ as a ||gram.

Niranjan Khanderia - 5 years, 1 month ago

Triangle With Squares!

If you're interested, here is follow up question .

The answer is 90.

1 solution

0 pending reports