Triangles (1).
The lengths of tangents drawn from A , B , and C to the incircle ( Σ ) of △ A B C are 8 , 6 , and 3 , respectively. The lengths of the parts of the tangents which are drawn parallel to sides B C , C A , and A B and intercepted between the sides of the triangle are p , q , and r , respectively.
Find the value of ∣ ∣ ∣ ∣ p − q − r p + q + r ∣ ∣ ∣ ∣ .
This figure is for representative purposes only.
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Good solution bro. But your approach is too straightforward. Such as how one comes from here
Also length of tangent from vertex A = semi-perimeter of triangle ADE
to here
i.e. 8 = 2 a c ⋅ p + a b ⋅ p + p
needs to be explained via similarity of triangles. I understand that you're constricted to the point due to less tools. Here are some things i can help you with for future solutions:
Log in to reply
Too long to write
Log in to reply
Well thank u for providing me with these tools
Log in to reply
@A Former Brilliant Member – You're welcome. :)
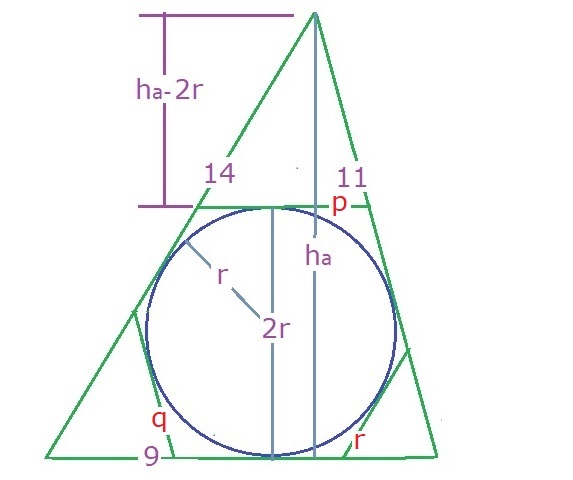
c = 8 + 6 = 1 4 , . . . . . . . . . . . . . . a = 6 + 3 = 9 , . . . . . . . . . . . . b = 8 + 3 = 1 1 , s = 1 / 2 ∗ ( a + b + c ) = 1 7 A r e a = s ∗ ( s − a ) ∗ ( s − b ) ∗ ( s − c ) = 4 9 . 4 7 9 3 . i n − r a d i u s , r = s 2 ∗ A r e a = 2 . 9 1 0 4 3 . A l t i t u d e s h a = a 2 ∗ a r e a = 9 2 ∗ 4 9 . 4 7 9 3 = 1 0 . 9 9 5 4 . A l t i t u d e s h b = b 2 ∗ a r e a = 1 1 2 ∗ 4 9 . 4 7 9 3 = 8 . 9 9 6 2 4 . A l t i t u d e s h c = c 2 ∗ a r e a = 1 4 2 ∗ 4 9 . 4 7 9 3 = 7 . 0 6 8 4 7 . ∴ p = h a a ∗ ( h a − 2 r ) = 1 0 . 9 9 5 4 9 ∗ ( 1 0 . 9 9 5 4 − 5 . 8 2 0 8 6 ) = 4 . 2 3 5 4 5 . ∴ q = h b a ∗ ( h b − 2 r ) = 8 . 9 9 6 2 4 9 ∗ ( 8 . 9 9 6 2 4 − 5 . 8 2 0 8 6 ) = 3 . 8 8 2 5 9 . ∴ r = h c a ∗ ( h c − 2 r ) = 7 . 0 6 8 4 7 9 ∗ ( 7 . 0 6 8 4 7 − 5 . 8 2 0 8 6 ) = 2 . 4 7 0 9 7 . S o p − q − r p + q + r = 5 .
Let the side of the triangles be represented by a, b & c
Therefore length of tangent from vertex A is equal to s-a and similarly s-b and s-c from vertices B & C respectively
Given s-a = 8, s-b = 6, s-c = 3 Adding the three we get
3s-(a+b+c) = 17 therefore s = 17
thus a = 9, b = 11, c = 14
Also length of tangent from vertex A = semi-perimeter of triangle ADE
i.e. 8 = 2 a c . p + a b . p + p
which gives p = a + b + c 1 6 a
therefore q = a + b + c 1 2 b r = a + b + c 6 c
thus ∣ ∣ ∣ p − q − r p + q + r ∣ ∣ ∣ = ∣ ∣ − 7 2 3 6 0 ∣ ∣ = 5