Triangles Being Fair

Let $\overline{AB}=1$ . Then $b=\overline{EF}=\dfrac{1}{\sqrt{2}}$ , since it is a side of a triangle with half the area.

Define $a=\overline{FC}$ , and get $\overline{EC}=1-a$ .

Apply law of cosines to $\triangle EFC$ to get an equation for $a$

$b^2=\dfrac12=a^2+(1-a)^2-2a(1-a)\cos60^\circ$

Simplify to $6a^2-6a+1=0$

And solve $a=\dfrac12+\dfrac{\sqrt3}{6}$ or $a=\dfrac12-\dfrac{\sqrt3}{6}$ .

If $\overline{FC}$ is the former, then $\overline{EC}$ will be the latter (and the smaller of the two).

Within $\triangle EFC$ , angle $x$ can be obtained from the law of sines $\dfrac{\sin x}{\frac12-\frac{\sqrt3}{6}}=\dfrac{\sin60^\circ}{\frac{1}{\sqrt2}}$

$x=\arcsin\left(\dfrac{\sqrt3-1}{2\sqrt2}\right)=\boxed{15^\circ}$

(This solution was improved using Calvin Lin's suggestion, see comment below. My original solution compared the area of $\triangle EFC$ calculated as a sixth of the area of $\triangle ABC$ to the same area calculated using two sides and an angle to produce the equation for $a$ .)

A solution based on a 30-60-90 triangle at a corner that connects the given areas to the side lengths and the angle. This approach limits the dependence on trigonometry to the definition of sine and use of the arcsin to obtain the angle.

Also a write up of a solution above that avoids the use of the arcsin function to get the angle. (However, arranging to the get a very familiar value of sine that we recognize allowing the reader to perform the arcsin function "by inspection" seems to amount to doing the same thing. One way or another it is still trigonometry at work here.)

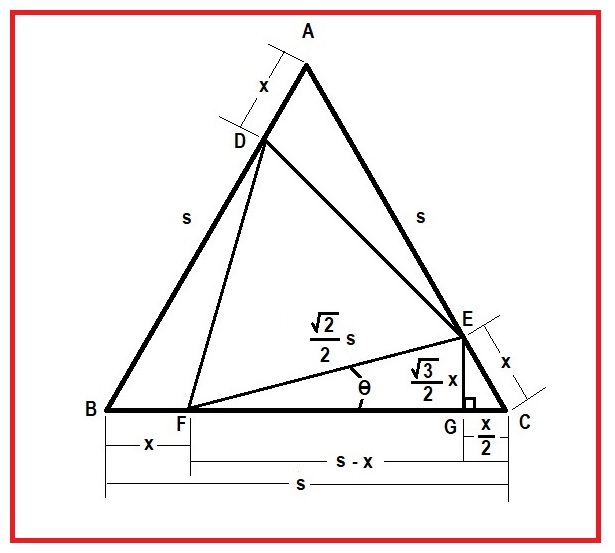
Let s be the side length of $\bigtriangleup ACB$ , x be the shortest distance from a corner of $\bigtriangleup ACB$ to a corner of $\bigtriangleup DEF$ , and $\theta$ = $\angle EFC$ as shown in the diagram above.

From given information Area $\bigtriangleup ACB$ = $\frac { \sqrt { 3}} {4} s^2$ , Area $\bigtriangleup DEF$ = $\frac{1}{2}$ Area $\bigtriangleup ACB$ = $\frac { \sqrt { 3}} {8} s^2$ , Area $\bigtriangleup ECF$ = $\frac{1}{6}$ Area $\bigtriangleup ACB$ = $\frac { \sqrt { 3}} {24} s^2$ and $\overline {EF}$ = $\frac {\sqrt{2}}{2} s$ .

Construct the perpendicular $\overline {EG}$ as shown to form a 30-60-90 triangle, $\bigtriangleup ECG$ from which it follows that

(1) $\space \space$ $\sin \theta = \frac { \frac {\sqrt {3}}{2}x } {\frac {\sqrt{2}}{2}s}$ = $\frac {\sqrt {3}}{\sqrt{2}} \frac {x}{s}$ = $\frac {\sqrt{6}}{2} \frac {x}{s}$ and $\angle EFC$ = $\arcsin( \sin \theta )$

The value of x can be found using the side and area relationships as follows:

Area $\bigtriangleup ECF$ = $\frac { \sqrt { 3}} {24} s^2$ = $\frac{1}{2}$ $s - x$ $\frac{\sqrt{3}}{2}x$ yields the equation $0 = x^2 -sx + \frac{s^2}{6}$

This equation has two roots a = $\frac{ s ( 3 + \sqrt{3})}{6}$ and b = $\frac{ s ( 3 - \sqrt{3})}{6}$

Using x = b in (1) gives the solution $\angle EFC = 15^\circ$

Using x = a in (1) gives $\theta = 75^\circ$ that is $\angle DFC$ corresponding to the other corner of $\bigtriangleup DEF$ at D.

Note that the roots sum to 1. Both are the lengths of line segments on a side of the outer triangle.

Put members of∆ ABC = m and k for ∆ EFD . area of blue zones = area of yellow zones so .5×m^2×√3\2 - .5×k^2×√3\2=.5×k×k×√3\2 so m=√2.k from geometry of the triangles ad=bf=ec=y as blue area =yellow so {√3÷4}.k^2=3×.5×y×(√2.k-y)×(√3÷2) so. k^2=3√2.ky-3y^2 ,, y^2-√2ky+(k^2÷3)=0. K Is constant so by solving the equation y=((√3-1)÷√6).k or( (√3+1)÷√6).k rejected as y must be less than k so y=.298858490k , at ∆ efc put angle (efc)=h cos(h)=k^2+(1.115507k)^2-(.298858490k)^2÷(2.k.(1.115507k)). So h=15°######