Triangles triangles

Relevant wiki: Length and Area - Composite Figures

Consider only the upper right part. It is completely made of the shape depicted below, in various scales: Notice how the blue area is only a third of the total area of this shape (1 of 3 equal areas is blue). Thus, the area above is $\frac{1}{3}$ blue.

But it's only half the total area. The other half is all blue, thus $\frac{1}{2}+\frac{1}{2}·\frac{1}{3}=\frac{2}{3}$ of the total area are blue.

Relevant wiki: Geometric Progression Sum

Let the square to have an area of 1 and a shaded triangle be $a_n$ for $n \in \mathbb N$ , where $a_1$ being the largest and smaller as $n$ increases. We note that $a_{n+1} = \frac 14 a_n$ . Then the shaded area is:

$\begin{aligned} A & = a_1 + a_2 + a_3 + \cdots \\ & = \frac 12 + \frac 14 \cdot \frac 12 + \left(\frac 14\right)^2 \frac 12 + \cdots \\ & = \frac 12 \left(1 + \frac 14 + \frac 1{4^2} + \cdots \right) \\ & = \frac 12 \left(\frac 1{1-\frac 14}\right) \\ & = \frac 12 \left(\frac 43 \right) \\ & = \frac 23 \end{aligned}$

The shaded fraction of the square $=\dfrac A1 = A = \boxed{\dfrac 23}$ .

Relevant wiki: Geometric Progression Sum

We can divide the square into two triangles as in the shape below. 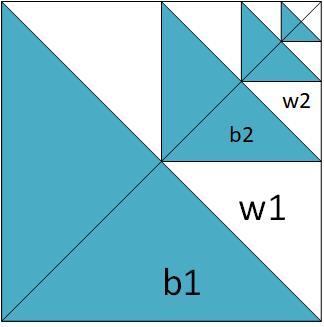now we can see that B1 = 2 W1, B2= 2 W2, ......... , Bn=2 Wn So sum B = 2 Sum W >>>>> Sum W = 0.5 Sum B Area of the square (A) = Sum B + Sum W = Sum B + 0.5 Sum B = 1.5 Sum B Ratio = (Sum B) / A = Sum B / 1.5 Sum B = 1/1.5 = $\frac{2}{3}$

The square has a blue half, and each subsequent blue triangle is a quarter the size of the last. This can be seen by noticing that each blue triangle makes up one quarter of a bigger white triangle which is equal in size to the previous, larger blue triangle. Therefore, if the total area of the square is 1 and the blue area is $x$ , then $x = \sum\limits_{n=0}^\infty \frac{1}{2*4^n}=\frac{1}{2}+\frac{1}{8}+\frac{1}{32}+\frac{1}{128}...$ $4x=4(\frac{1}{2}+\frac{1}{8}+\frac{1}{32}+\frac{1}{128}...)=2+\frac{1}{2}+\frac{1}{8}+\frac{1}{32}+\frac{1}{128}...$ It can be seen that $4x$ is equal to 2 plus the original $x$ , so $4x=x+2$ $4x-x=2$ $3x=2$ $x=\frac{2}{3}$

Here is the multiple choice test taker’s way to solve the problem. Looking at the picture you know blue shaded area fills at least half the squares do the white portion fills at least one fourth of the square. Therefore the answer must lie between 1/2 and 3/4. As only one of the choices is greater than 1/2 and less than 3/4 then 2/3 must be the correct answer. Estimation, the test takers friend!

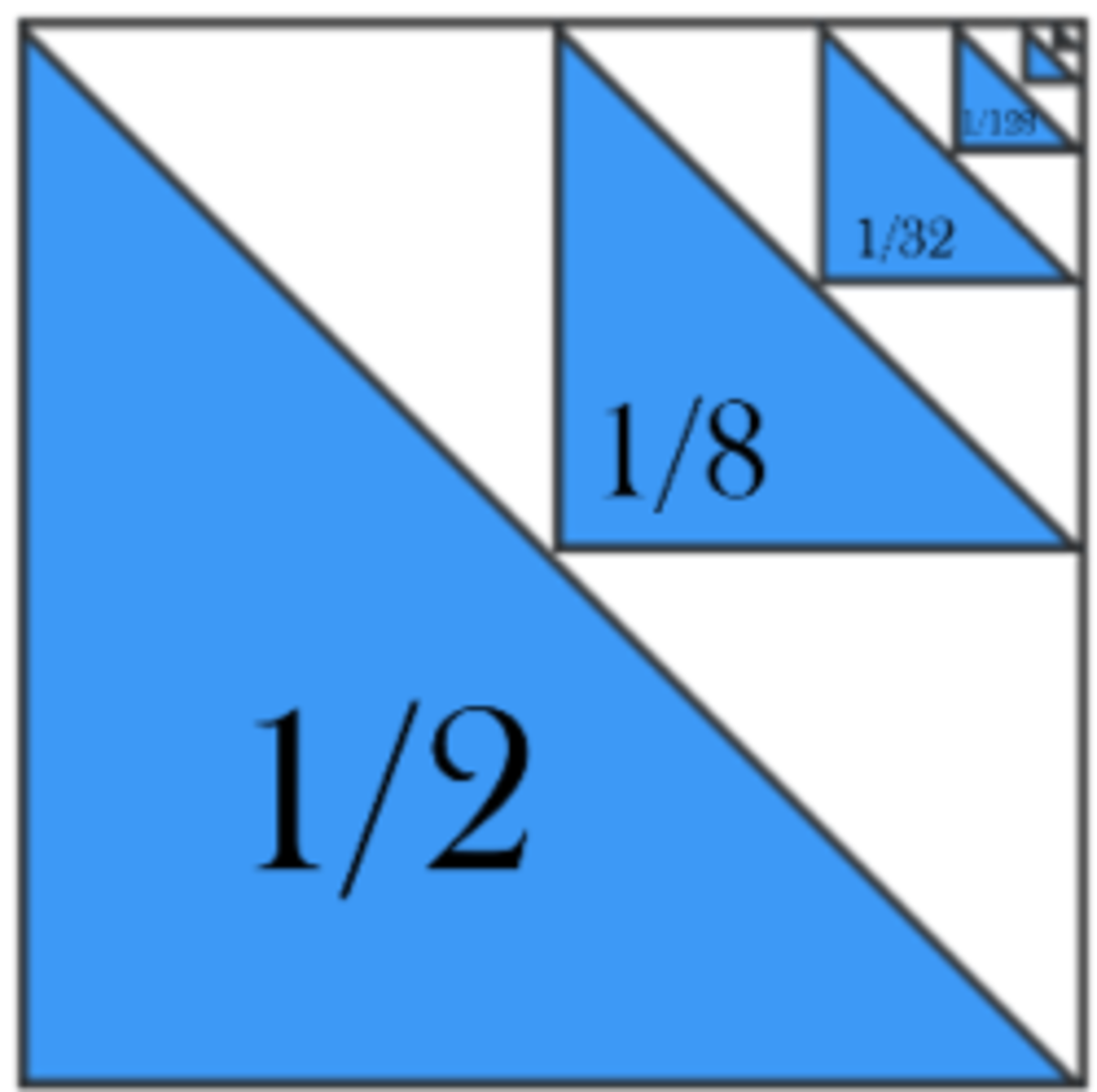
By observing each of the shaded triangles, one can deduce that the shaded areas are 1/2, 1/8, 1/32 and so on. By setting the area of the square that is shaded to x, you create the following equation: x= $\frac{1}{2}$ + $\frac{1}{8}$ + $\frac{1}{32}$ ...

Although this equation is infinite in length, x will be a finite answer. But how do we solve for the x if the equation is infinite? Well by looking at the equation, you may notice that each term is one-fourth of the previous term: $\frac{1}{8}$ = $\frac{1}{2}$ $\frac{1}{4}$ $\frac{1}{32}$ = $\frac{1}{8}$ $\frac{1}{4}$

Because of this, we can multiply both sides of: x= $\frac{1}{2}$ + $\frac{1}{8}$ + $\frac{1}{32}$ ...

to get: 4x=1+ $\frac{1}{2}$ + $\frac{1}{8}$ + $\frac{1}{32}$ ...

See something familiar? That's right. Both equations have $\frac{1}{2}$ + $\frac{1}{8}$ + $\frac{1}{32}$ ... Therefore, we can subtract the first equation from the second equation to get: 3x=2

This means that by dividing both sides of 3 you get: x= $\frac{2}{3}$

The biggest triangle forms 1/2 of the square. The next triangle forms 1/8 of the square, The next triangle forms 1/16 of the square and so on.... So it forms a G.P. With first term=1/2 and common difference=1/4 So sum of the G.P. Is 1/2 divided by 1-1/4 = 2/3

This is a summation of geometric progression to the infinity, given the formula a/(1-r) where a= first term and r= common ratio of the progression. So in this case a would be 1/4 and r would be 1/4. So substituting the values into the formula will give us 2/3.

The sum of all blue shaded triangles is the sum of the infinite sequence:

$\begin{array}{lcl} S & = & 1/2 + 1/2^3 + 1/2^5 + 1/2^7 + . . . \end{array}$

If you multiply this sequence by 4, in order to remove the first fraction, one gets:

$\begin{array}{lcl} 4S & = & 2^2/2 + 2^2/2^3 + 2^2/2^5 + 2^2/2^7 + . . . \end{array}$

$\begin{array}{lcl} 4S & = & 2 + 1/2 + 1/2^3 + 1/2^5 + 1/2^7 + . . . \end{array}$

Now, this 4S looks similar to S doesn't it? Let's subtract:

$\begin{array}{lcl} 4S & = & 2 + 1/2 + 1/2^3 + 1/2^5 + 1/2^7 + . . . \end{array}$

$\begin{array}{lcl} S & = & 1/2 + 1/2^3 + 1/2^5 + 1/2^7 + . . . \end{array}$

3S = 2, and thus S=2/3

Notice that the big square is copied and pasted into 1/4 of the original. This is continued infinitely as each succeeding image is 1/4 of the previous one. The biggest blue area is 1/2 of the shape. The next area down is 1/2 of the smaller square that is 1/4 of the size of the original. The next blue area is 1/2 of the next smaller square that is 1/4 of the size of the previous square which is 1/4 of the original (in other words it is 1/2 of 1/4 of 1/4). This process continues as an infinite series:

Blue area = A = 1/2 + 1/2 (1/4) + 1/2 (1/4)(1/4) + 1/2*(1/4)(1/4)(1/4) + ...

A= (1/2) (1/4)^0 + (1/2) (1/4)^1 + (1/2) (1/4)^2 + (1/2) (1/4)^3 + ...

A = (1/2) * (1 + 1/4 + 1/16 + 1/64 + ...)

2A = 1 + 1/4 + 1/16 + 1/64 + ...

Now multiply 2A by 1/4: 2A * (1/4) = 1/4 + 1/16 + 1/64 + ...

Notice that this is the same as 2A - 1 2A -1 = 1/4 + 1/16 + 1/64 + ...

Therefore, 2A*(1/4) = 2A-1

Use algebra to solve for A: (3/2)A=1

Therefore, Blue area = A = 2/3.

The area can be described with the formula $A=1/2+A/4$ . If you replace A with something and the left side is smaller than the right, then you picked an A which is too small. If the left side is bigger, then you picked an A which is too big.

I do however not know any way of solving these types of formulas other than trying a lot of values for A :P