Triangular Kenmotu
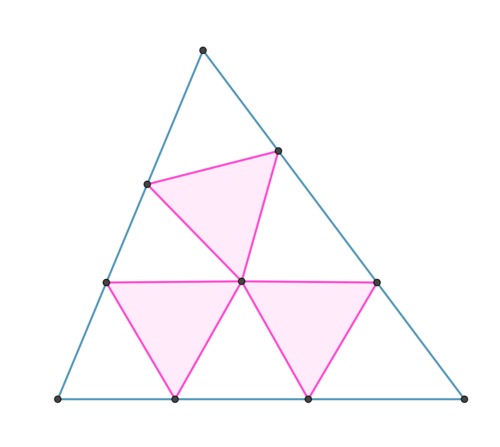
Three congruent equilateral triangle, sharing a common vertex, are inscribed in △ A B C with the other two vertices of each equilateral triangle touch the sides of △ A B C of lengths 1 3 , 1 4 , and 1 5 .
If the side length of the equilateral triangle is d a b + c , where a , c and d are coprime integers and b is square-free integer, submit a + b + c + d .
Similar Problems:
The answer is 26854.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Thank you for the detailed solution.
Log in to reply
@Maria Kozlowska Is point X in your figure the 2nd Kenmotu Point? i.e. is it X(372) in The Encyclopedia of Triangle Centers here ? It doesn't seem to have the same trilinear coordinates.
Log in to reply
No. Common vertex is triangle center X(15) which is First Isodynamic Point .
It is Isogonal Conjugate of Fermat point. The point can be constructed by creating equilateral triangles outward on triangle sides and connecting outermost points to the opposite vertices of the triangle (Napoleon theorem). This will produce Fermat point. Then the connecting lines need to be reflected on angle bisectors of corresponding angles. This will produce point X(15).
To check triangle center this page can be used.
Log in to reply
@Maria Kozlowska – Aha, that makes perfect sense. Thank you!
@Thanos Petropoulos , of course I used the same method.
I wonder if there's a way to automatically solve these sort of problems. I'm attempting to use sympy to define the problem and then solving symbolically but it's taking really really long. If it works I'll post a solution.
Log in to reply
I have generalized the solution in Pentagonal Kenmotu as follows:
r = a cos 2 α + b cos 2 β + c cos 2 γ 2 Δ where ⎩ ⎪ ⎨ ⎪ ⎧ α = 2 A − θ β = 2 B − θ γ = 2 C − θ
You can take a look.
Log in to reply
Cool! I am attempting to find a more general programming approach for any of these 'inscribing problems'. Though I'm seeing less point in writing one now since I did not know that a symbolic geometry solver already existed (It already does).
Log in to reply
@Julian Poon – I've been looking for such a solver too. What is it? Free?
Log in to reply
@Fletcher Mattox – I attempted using the module Sympy.geometry. However, I've not been able to define the problem ia a way that's been solvable by sympy. The best ive done for this problem is 10 constraints. It could of course be improved drastically specific to this problem but I attempted to formulate in such a way that's general. Either ways, 10 constraints took forever to solve and i never got an output.
I've not attempted using better solvers such as Mathematica.
In all these kenmotu problems, the three 'tip' triangles are similar to each other and to the 'big' triangle with proper orientation. In this case, Δ A B C ∼ Δ A J O ∼ Δ L K C ∼ Δ M B P . Also, in this particular case, the Kenmotu point is actually the isodynamic point of the triangle. Unfortunately, this doesn't help simplify the calculation in any way.:(
Let ∠ L X M = α , ∠ K X J = β , and ∠ O X P = γ (figure 1). We note that ∠ X P O = 9 0 ∘ − 2 γ , hence, ∠ M P B = 1 8 0 ∘ − ( 9 0 ∘ − 2 γ ) − 6 0 ∘ = 2 γ + 3 0 ∘ , thus, ∠ L M X = ∠ L M P − 6 0 ∘ = ( 2 γ + 3 0 ∘ + B ) − 6 0 ∘ = B + 2 γ − 3 0 ∘ .
Consequently, α = 1 8 0 ∘ − 2 ⋅ ∠ L M X = 1 8 0 ∘ − 2 ( B + 2 γ − 3 0 ∘ ) = 2 4 0 ∘ − 2 B − γ .
Similarly, β = 2 4 0 ∘ − 2 A − γ .
Moreover, α + β + γ + 3 × 6 0 ∘ α + β + γ 2 4 0 ∘ − 2 B − γ + 2 4 0 ∘ − 2 A − γ + γ = 3 6 0 ∘ = 1 8 0 ∘ = 1 8 0 ∘
⇒ γ = 3 0 0 ∘ − 2 ( A + B ) = 3 0 0 ∘ − 2 ( 1 8 0 ∘ − C ) = 2 C − 6 0 ∘ ⇒ 2 γ = C − 3 0 ∘ Similarly, 2 α = A − 3 0 ∘ and 2 β = B − 3 0 ∘ .
Using Heron’s formula we find the area of △ A B C : [ A B C ] = 8 4 .
Let the side length of the equilateral triangles be s and the altitudes from X to B C , C A and A B be h a , h b , and h c respectively. Then the area of △ A B C is also given by: 2 h a ⋅ B C + h b ⋅ C A + h c ⋅ A B 2 1 ( 1 5 s cos 2 α + 1 3 s cos 2 β + 1 4 s cos 2 γ ) = [ A B C ] = 8 4 ( 1 )
In order to calculate cos 2 α , cos 2 β and cos 2 γ , we first find the sines and cosines of the angles of △ A B C .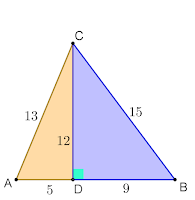 Figure 2
Figure 2
We notice that △ A B C is a compound of a 5 - 1 2 - 1 3 and a 9 - 1 2 - 1 5 right-angled triangle (figure 2).
Thus, it is easy to find that cos A = 1 3 5 , sin A = 1 3 1 2 , cos B = 1 5 9 , sin B = 1 5 1 2 .
By sine law, 1 4 sin C = 1 5 sin A ⇒ sin C = 1 5 1 4 ⋅ 1 3 1 2 ⇒ sin C = 6 5 5 6 .
cos C = 1 − sin 2 C = 1 − ( 6 5 5 6 ) 2 ⇒ cos C = 6 5 3 3
Combining the results obtained, we get
cos 2 α = cos ( A − 3 0 ∘ ) = cos A ⋅ cos 3 0 ∘ + sin A ⋅ sin 3 0 ∘ = 1 3 5 ⋅ 2 3 + 1 3 1 2 ⋅ 2 1 = 2 6 1 2 + 5 3 Similarly, cos 2 β = cos ( B − 3 0 ∘ ) = 1 0 4 + 3 3 cos 2 γ = cos ( C − 3 0 ∘ ) = 1 3 0 5 6 + 3 3 3 Finaly, ( 1 ) ⇒ s [ 1 5 ⋅ 2 6 1 2 + 5 3 + 1 3 ⋅ 1 0 4 + 3 3 + 1 4 ⋅ 1 3 0 5 6 + 3 3 3 ] = 8 4 ⋅ 2 which solves to s = 1 8 1 − 3 5 2 8 0 3 + 6 1 9 5 0 for the answer, a + b + c + d = − 3 5 2 8 0 + 3 + 6 1 9 5 0 + 1 8 1 = 2 6 8 5 4 .