Triangular Tan Tutu
In △ A B C with sides a , b , and c (with c opposite to ∠ C ), if tan C = − 2 and a + b − c = 2 , then the inradius r is a root of f ( x ) = x 2 + m x + n , where m and n are integers. Find m + n .
The answer is -2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Nice solution! I think you have a typo on the first line: D is the common point of the incircle and the side a, not C.
The trick here will be to avoid calculating a , b explicitly, and just use symmetric functions. We already have a + b = c + 2 from the question.
From tan C = − 2 we get cos C = − 5 1 and sin C = 5 2 .
Using the cosine rule, c 2 c 2 c 2 c 2 a b = a 2 + b 2 − 2 a b cos C = a 2 + b 2 + 5 2 a b = ( c + 2 ) 2 − 2 a b + 5 2 a b = c 2 + 4 c + 4 − 2 a b + 5 2 a b = 1 − 5 1 2 ( c + 1 ) = 2 1 ( 5 + 5 ) ( c + 1 )
The area of the triangle is Δ = 2 1 a b sin C = 4 1 ( 5 + 5 ) ( c + 1 ) 5 2 = 2 1 ( 1 + 5 ) ( c + 1 )
and the semiperimeter is s = 2 a + b + c = c + 1
so the inradius is r = s Δ = 2 1 ( 1 + 5 )
which is the golden ratio and is a root of x 2 − x − 1 = 0 , giving the answer m + n = − 1 − 1 = − 2 .
There are actually infinitely many triangles that fit these conditions (which makes sense - three pieces of information are needed to define a triangle, and we only have two). There's a restriction on c , though, which I'll leave as a bonus question.
I'm guessing there's another solution here that uses the fact that the distance from C to the two nearest points of tangency of the triangle to its incircle are both 1 .
I wonder if it's possible to set up a similar problem where the inradius can be either one of the two roots of a quadratic?
Log in to reply
c is a minimum when a = b , so c 2 = a 2 + b 2 + 5 2 a b = ( 2 + 5 2 ) a 2 , and c + 2 = a + b = 2 a . Combining these and solving gives c = 3 + 5 + 2 5 + 5 ≈ 1 1 . 3 9 1 . So the restriction on c is that c > 1 1 . 3 9 1 .
The problem was inspired when I derived the following formula for the inradius r :
r = P 2 A = a + b + c 2 ⋅ 2 1 a b sin C = ( a + b + c ) ( a + b − c ) a b sin C ⋅ ( a + b − c ) = a 2 + 2 a b + b 2 − c 2 a b sin C ⋅ ( a + b − c ) = a 2 + 2 a b + b 2 − ( a 2 + b 2 − 2 a b cos C ) a b sin C ⋅ ( a + b − c ) = 2 a b ( 1 + cos C ) a b sin C ⋅ ( a + b − c ) = 2 1 ( a + b − c ) tan 2 1 C
To me the picture in Thanos's solution helps make this equation make sense.
Also there are infinitely many quadratic equations with a root the golden ratio, but only one of them has an integer m and n.
Given that tan C = − 2 , ⟹ sin C = 5 2 and cos C = − 5 1 . By cosine rule ,
c 2 c 2 c 2 c 2 ⟹ 2 c + 2 = a 2 + b 2 − 2 a b cos C = ( a + b ) 2 − 2 a b + 5 2 a b = ( c + 2 ) 2 − 2 ( 1 − 5 1 ) a b = c 2 + 4 c + 4 − 2 ( 1 − 5 1 ) a b = ( 1 − 5 1 ) a b Since a + b − c = 2
The inradius r is given by:
r = 2 1 ( a + b + c ) Δ = 2 1 ( a + b + c ) 2 1 a b sin C = a + b + c 5 2 a b = 2 c + 2 5 2 a b = ( 1 − 5 1 ) a b 5 2 a b = 2 1 + 5 = φ where Δ is the area of △ A B C where φ denotes the gold ratio.
Therefore r = φ is the root of f ( x ) = x 2 − x − 1 . The required answer is m + n = − 1 − 1 = − 2 .
x 2 − ( φ + 1 ) x + φ = 0 ⇒ x = 1 o r x = φ ⇒ m + n = − 1
Log in to reply
Nope, φ 2 − φ − 1 = 0 .
Log in to reply
But why exactly x 2 − x − 1 , since there are infinitely many quadratic equations with a root φ ?
Log in to reply
@Iliya Hristov – Are there many quadrilateral equations? Come up with another one please. m and n must be integers. φ is irrational and not an integer.
Log in to reply
@Chew-Seong Cheong – Precisely x 2 − x − 1 = 0 is the only quadratic equation with a root φ and integer m and n.
Log in to reply
@Iliya Hristov – Then why were you asking?
Log in to reply
@Chew-Seong Cheong – Because for me it is not an obvious fact and no one else even try to prove it.
Log in to reply
@Iliya Hristov – It is clearly given in the question that m and n are integers. It is just that someone is too clever and did not see it.
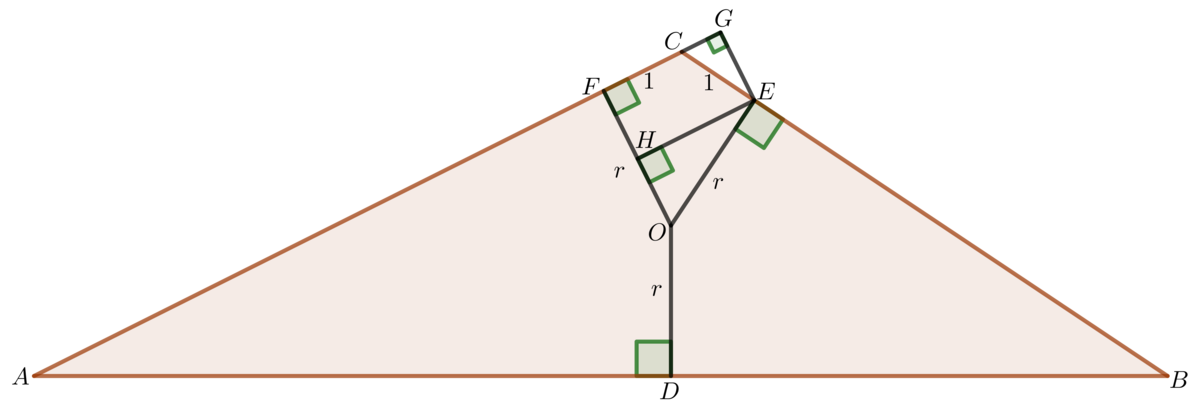 B
C
=
a
C
A
=
b
A
B
=
c
O
D
=
O
E
=
O
F
=
r
C
E
=
C
F
=
2
a
+
b
−
c
=
2
2
=
1
tan
C
=
−
2
⇒
9
0
∘
<
C
<
1
8
0
∘
a
n
d
G
E
=
2
G
C
G
C
2
+
(
2
G
C
)
2
=
1
2
⇒
G
C
=
5
1
△
C
E
G
∼
△
O
E
H
⇒
1
G
E
=
r
H
E
⇒
5
2
=
r
1
+
5
1
⇒
r
=
2
1
+
5
x
2
+
m
x
+
n
=
0
⇒
(
2
1
+
5
)
2
+
m
2
1
+
5
+
n
≡
0
⇒
4
1
+
2
5
+
5
+
2
m
+
m
5
≡
−
n
⇒
(
m
+
1
)
5
+
m
+
3
≡
−
2
n
⇒
(
m
+
1
)
=
0
⇒
m
=
−
1
⇒
−
1
+
3
=
−
2
n
⇒
n
=
−
1
⇒
m
+
n
=
−
2
B
C
=
a
C
A
=
b
A
B
=
c
O
D
=
O
E
=
O
F
=
r
C
E
=
C
F
=
2
a
+
b
−
c
=
2
2
=
1
tan
C
=
−
2
⇒
9
0
∘
<
C
<
1
8
0
∘
a
n
d
G
E
=
2
G
C
G
C
2
+
(
2
G
C
)
2
=
1
2
⇒
G
C
=
5
1
△
C
E
G
∼
△
O
E
H
⇒
1
G
E
=
r
H
E
⇒
5
2
=
r
1
+
5
1
⇒
r
=
2
1
+
5
x
2
+
m
x
+
n
=
0
⇒
(
2
1
+
5
)
2
+
m
2
1
+
5
+
n
≡
0
⇒
4
1
+
2
5
+
5
+
2
m
+
m
5
≡
−
n
⇒
(
m
+
1
)
5
+
m
+
3
≡
−
2
n
⇒
(
m
+
1
)
=
0
⇒
m
=
−
1
⇒
−
1
+
3
=
−
2
n
⇒
n
=
−
1
⇒
m
+
n
=
−
2
Nice solution!
tan C = − 2 ⇒ 1 − ( tan 2 C ) 2 2 tan 2 C = − 2 ⇒ 1 − t 2 t = − 1 ⇒ t 2 − t − 1 = 0 ( 1 ) Moreover, tan 2 C = C D I D ⇒ t = 1 r ⇒ t = r Combining with ( 1 ) we get r 2 − r − 1 = 0 Thus, m = n = − 1 and the answer is m + n = − 2 .