Tricircles
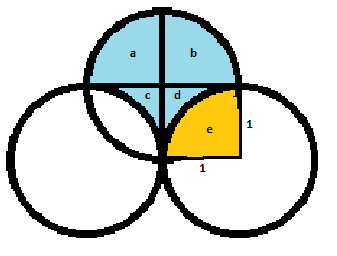
I have 3 unit circles. Two of them are externally tangent to each other, and the third one passes through the tangent point, cutting two symmetrical areas from the two circles, as shown above. What is the shaded area?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
I believe the question is not worded quite right. The third circle can pass through the tangent but necessarily remain symmetrical around it. The solution requires it also be symmetrical.
Log in to reply
I agree that the question should include something about its assumed symmetry that is in the picture. If it weren't symmetrical, an extreme case would be that the third circle completely overlaps the second circle (still making it pass through the tangent point) making the shaded area equal to zero.
Log in to reply
Yes. It should be stated that the third circle's center is equidistant from the centers of the tangent circles
If you read carefully the text of the problem, then you can find: "...cutting two symmetrical areas from the two circles..." So, please read before writing.
Log in to reply
The problem must have been updated (and improved). The phrase "cutting two symmetrical areas from the two circles" was not there a few days ago.
You have made assumptions based on a drawing. Symmetry is not a measure. You must prove that the "crosshairs" in the shaded circle are right angles. Symmetry does not imply angular equality. You assume that the horizontal line is exactly equal to the vertical line. This is not known.
Log in to reply
Proved more rigorously, let O be the center of the top circle, P be the center of the left circle, Q be the center of the right circle, A be the left intersection of circles O and P , B be the right intersection of circles O and Q , and C be the intersection of all three circles. Since all three circles are unit circles, O A = O B = O C = P A = P C = Q C = Q B = 1 . Also, since circle O cuts two symmetrical areas from the two circles, A C ≅ B C . Then △ A P C ≅ △ A C O ≅ △ B C O ≅ △ B C Q by SSS, and ∠ A P C ≅ ∠ A C O ≅ ∠ B C O ≅ ∠ B C Q by corresponding parts. Since circle P and circle Q are externally tangent to each other, ∠ P C Q is a straight line equaling 1 8 0 ° , meaning m ∠ A P C = m ∠ A C O = m ∠ B C O = m ∠ B C Q = 4 5 ° . Since △ O A C is an isosceles triangle, m ∠ C A O = 4 5 ° and using the angle sum of △ A O C , m ∠ A O C = 9 0 ° . A similar argument will show that m ∠ B O C = 9 0 ° .
Therefore, the "crosshairs" in the shaded region are right angles, and the horizontal line segment in the shaded region is exactly equal to the vertical line segment in the shaded region.
Are you assuming r=1 or the answer would be 2r?
Log in to reply
I think because they are unit circles, it can be assumed that there radii are equal to one.
Elegant solution... And yes the question does imply symmetry
great solution and awesome visualization!!
Wow!!! Elegant approach.
Beautiful!!!! Geometry using geometry.....
Question not worded properly
Cut and then put the parts together
The area of the shape is equal to the area of a square inscribed in a unit circle, that is a square with side
2
and area
2
.
How do you conclude that the length of the side of the square is √2
Log in to reply
Because the square can be divided into 4 right triangles, each with 2 sides adjacent to a right angle with length 1. The sides (hypotenuses/hypoteni?) marked with 1,2,3,4 above would be the square root of the sum of the squares of those adjacent sides.
Since it is a unit circle we know the radius is 1. Divide the square into four equal triangles that each have the radii as two sides and an edge of the square as a third side. Then use pythagorean theorem. If 1^2 + 1^2 = X^2 then X = square root of 2
I really don't see where I went wrong. I also worked with segments. 4 segments x (PI*r^2/4 + 1/2 bh)= PI -2 That's for quarter of a circle. But I get the same answer if I use 2x(half circle area - triangle with base 2 and height 1). I must be going crazy.....
Rather odd... Finding an integer as the area of a region clearly dependent on Pi.
T. Garza
At first it's hard to understand why quadrangle is a square,but after proving it is, this way of solving problems becomes quite smart
area of region "d" = area of square (d+e) - area of circular sector(e) = 1 − 4 π
therefore area of a+b+c+d = 2 x area of b+d = 2 × ( 4 π + ( 1 − 4 π ) ) = 2
This seems less intuitive and more like a proof. Upvoting this solution.
Log in to reply
thats because intuitive solutions were already available ..
I'm using the area equation and I got 2 r^2 as the answer....
I was misled by the term "unit circles." I thought this meant circles of unit area, not of unit radius. I think the term "circles of unit radius" would have been a better one to use. (I'm not saying I'd have got the right answer though!!!!)
Might be pretty clear for most, but I took a while to wrap my head around how the (d+e) was area enclosed by a square. The line segments are all 1 unit in length and one of the angles can be proved to be 90 degrees as the angle between the radius and tangent is 90.
The question as emailed does not have a unique solution as it omits the crucial phrase "cutting two symmetrical areas from the two circles".
it does say 2 symmetrical areas
As the problem is described, the following case also applies:
which gives a total different result. So the folowing should be added to the problem description: The 3d circle must "cut the two other circles into 90-degree segments" (or "have the same radius with the two other circles"). In this case, the area of a segment is r^2
(π-2)/4 (result of area of a 90-degree segment). Two of them make a r^2
(π-2)/2, which form a "leaf". Subtracting two "leaves" from the total ara circle, we get: r^2
π - r^2
(π-2) = r^2
π - r^2
π + 2
r^2 = 2
r^2 = 2
The problem stated 3 unit circles. Doesn't that mean all three circles are the same size with an r=1?
Log in to reply
Yes, that is true, it is obvious as it states "3 unit circles".
why is 2r^2 = 2? do we replace r with 1?
Log in to reply
Yep. U may check my answer. it has the proof
This was stated in the problem: "3 unit circles"
That means that all 3 circles have radius = 1
Your 3 circles have different sizes.
Using the equation of a circle and the integral of the differece of two functions bounding a region gives directly the area of that region. Choosing the origine of the x- and y-axis to be the point of intersection of the two tangent circles and using the symetrical aspect of the problem one finds:
A r e a = 2 ⋅ ∫ 0 1 ( 1 + 1 − x 2 − 1 − ( x − 1 ) 2 ) d x = 2
Would you be able to provide an explanation using a double integral with r dr d(theta)? I attempted it but I couldn't find the right areas of integration for the radius (which I tried to let it go from 1 to cos^2(theta) + sin^2(theta) but to no avail).
Log in to reply
...(which I tried to let it go from 1 to cos^2(theta) + sin^2(theta) but to no avail).
cos 2 θ + sin 2 θ = 1 , which means your integral evaluates to 0. This suggests that your limits are wrong in the first place.
Log in to reply
Ahh, a stupid mistake... I tried it again but I'm unsure of the interval in which I should let r vary through. I am setting my origin at the center of the purple circle and I know r has to be from 1 (starting when theta = 0) along the path of the outer circumference of the two intersecting circles, my problem is simply trying to find this equation for when the circles intersect. Any help would be much appreciated!
Log in to reply
@Trevor Ohara-Oates – I think you're just finding an overcomplicated approach to a simple question. I don't think it's really fruitful to think about double integrals here.
Take a quarter circle. Area of which is pie/4. Area of triangle in this quarter circle is .5×1×1×sin 90% = .5 The are of the chord = pie/4 - .5 There are 4 of these in the circle. So multiply by 4 = pie -2. Area of full circle = pie. Hence shaded area is pie-(pie-2) = 2.
Area of this shape using any length for radius is equal to:
A = 2 r 2
Hence, inputting "1" gives 2
How to get this formula:
As you can see in the above image, the red lines represent the radius r ; I have made a square too. Clearly to understand that there is a quarter of a circle whose area is 4 π r 2 . Hence we can say that:
Area of the shape = Area of semi-circle + 2 times (the area of the square - the area of the quadrant) = 2 π r 2 + 2 ( r 2 − 4 π r 2 ) = 2 π r 2 + 2 r 2 − 2 π r 2 = 2 r 2
How do you get this???
Log in to reply
Sorry I will prove it soon.... I edited the answer
The shaded area can be split up into 4 regions with right angles and unit legs, and then rearranged into a 2 by 1 rectangle, as shown below.
Therefore, the area of the shaded region is the same as the area of the 2 by 1 rectangle, which is 2 .