Trick Clocks!

The minute hand goes around $24$ times in $24$ hours.

The hour hand goes around, in the same direction, $2$ times in $24$ hours.

Relative to the hour hand, the minute hand goes around $24-2=22$ times

assuming all the relative positions, including directly opposite each other, $\boxed{22}$ times.

There is one time during each hour except the 5 o'clock hour (and again during the 17:00s) because by the time the minute hand is directly across from the hour hand it is 6:00.

The the position measure from the 12 marking in degrees of the hour hand and minute hand after time $t$ be $\theta_h (t)$ and $\theta_m (t)$ respectively. Let time $t=0$ be 06:00 when the hour and minute hands are in a straight line or $180^\circ$ apart. Then $\theta_h (0) = 180$ and $\theta_m (0) = 0$ . Since the hour hand is moving at $30^\circ$ in one hour or 60 minutes, its angular speed is $\frac 12^\circ$ per minute, while that of the minute hand is $\frac {360}{60} = 6^\circ$ per minute. Then we have

$\begin{cases} \theta_h(t) = \dfrac t2 + 180 \\ \theta_m (t) = 6t \end{cases}$

And we need to find the number of times when $\theta_h (t) - \theta_m (t) \bmod 360 = 180$ , since the minute hand runs 12 times faster than the hour hand. Note that:

$\begin{aligned} \theta_h(t) - \theta_m (t) \bmod 360 & = 180 \\ \theta_h(t) - (\theta_m (t) - 360n) & = 180 & \small \color{#3D99F6} \text{where }n \text{ is an integer.} \\ \frac t2 + 180 - 6t + 360n & = 180 \\ \implies t_n & = \frac {720n}{11} & \small \color{#3D99F6} \text{in minutes} \\ & = \frac {12n}{11} & \small \color{#3D99F6} \text{ in hours} \end{aligned}$

We note that when $n=22$ , $t_{22} = 24$ hours. Therefore, there are $\boxed{22}$ times the hour and minute hands form a straight line.

The first time after $6:00$ that the hour and minute hand will form a $180^{\circ}$ angle will be shortly after $7:05$ ; the exact time is $5\frac{5}{11}$ minutes after $7$ o'clock, but it is not necessary to establish that. It will happen again shortly after $8:10, 9:15, 10:20$ etc for every hour until shortly after $4:50$ . However, there will be no such occurrence for the $5$ o'clock hour; if there were, it would have to happen shortly after $5:55$ , but we know the angle will be $180^{\circ}$ at $6:00$ , so there would have to be two such occurrences within a space of $5$ minutes, which is clearly impossible. So there will be $11$ occurrences over a twelve-hour period, or $\boxed{22}$ in a 24-hour day.

The answer is twice the number of times red lines cross black horizontal line on the graph below. 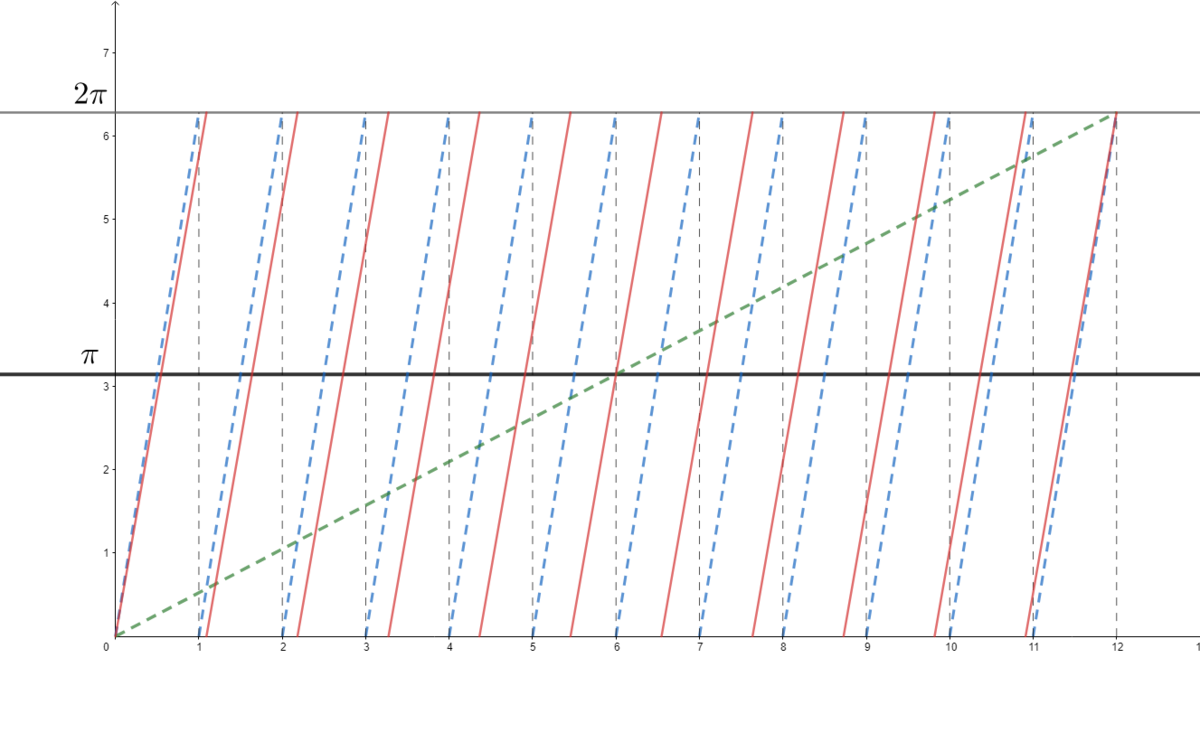Thus $2\times 11 = \boxed{22}$ .

Here are the equations represented on the graph: $\begin{aligned}&{\color{#456461} \phi_{h} = \frac{2\pi}{12}t(h)} \\ &{\color{#3D99F6} \phi_{m} = 2\pi t(h)} \\ &{\color{#D61F06} \Delta\phi = \phi_{m}-\phi_{h}}.\end{aligned}$

Just by visualizing all possible straight lines, we see that there is a straight line for after every hour besides 5pm. When you turn the minute hand after 5pm and try to form the next straight line, you see that the next straight line occurs at 6pm. The same happens again at 5am. Thus the answer is 24 -2 = 22

Let 6 degrees equal to 1point. In 60 minutes, minute hand moves 60 points, whereas hour hand moves 5 points. So relative speed of 2 hands is 60-5 = 55 points. At 12AM both hands make 0 degrees, to make 180 degrees b\w them they have to move 30 points relative to each other. Hence it will take 30/55 hrs to make 180 degrees for the first time. Next time they have to travel 60 points to make 180 degrees, which will take 60/55 hrs. So we can get the following equation 30/55+(60/55)n = 24 Where n= number of time when minute hand make 180degree with the hour hand after first time. n= 21.2 Total number in a day whey both hands makes 180 degrees = 21+1 =22

Each successive event requires 65 minutes + the extra movement of the hour hand past its hour. Minutes per day 1440 / 65 = 22.something, therefore the answer has to be 22.

This aproximation method works because we know the hands align back their starting position every 24 hours and the answer must be a whole number.

If we go back in time about 33 minutes from each such position, we reach a position where both hands coincide.

It's easy to see that this is a bijection, so the problem is reduced to the well-known problem of how many times the hands coincide in a 12 hour period (doubled to get the result for a 24 hour period).

Which can be easily seen to be 11 (one for each hour except the last).

Imagine the numbers on the clock are "unwinded" and stretched out, so that the numbers are on a straight line. We can imagine putting these numbers onto the interval x:[0,24]. Then the rate at which the hour hand moves can be modeled by the function h(x) = x, and the rate for the minute hand is m(x) = 12x. Because we are looking for when the hands form a long straight line, on the clock, this is represented by when the distance between the hands along the clock is exactly 6. Now because the clock is cyclic (it repeats the same numbers) and our graph is not, we need to evaluate the number of times the distance between the two hands is a multiple of 6, but not a multiple of 12 (because that would have the hands being in a short straight line). The distance between the hands is given by f(x) = m(x) - h(x) = 11x. Now we evaluate the number of times f(x) is a multiple of 6 but not 12, on the interval x:[0,24]. I simply evaluated this by counting, and came out with the answer, 22 .

Mathematically... (Base time units is minutes)

The angle of the hour hand = $\frac{PI}{360}$ t

The angle of the minute hand is $\frac{PI}{30}$ t

They are 180° apart when $\frac{PI}{360}$ t = $\frac{PI}{30}$ t + PI

Solving for t yields $\frac{360}{11}$

There are 1440 minutes in a day, and 1440 / (360/11) = 22 and some change

Every time the minute hand sweeps out an hour (a full rotation) it makes a 180 degree angle with the hour hand at some point during that rotation. Starting from midnight, count once as the hour hand goes from 12 to 1. Count again to go from 1 to 2 and so on until you get to noon. That gives eleven times that the hour and minute hand make a 180 degree angle (contrary to what most people are saying, this does happen during the transition from 5-6, it's just that the 180 degree angle is made at the very last moments of the hour, and then the next 180 degree angle during the transition from 6-7 happens immediately after when the clock strikes 6. In other words, they happen back to back). Do this one more time to get from noon to midnight and you get another eleven times to get a total of 22 times the hands are 180 degrees apart in a 24 hour period.

Every hour, this happens once. The one time it doesn't happen is the 5:00 and 17:00 because the time is 6:00 or 18:00 when it happens then. 24 - 2 is 22. Answer : $\boxed{22}$