Same Same, But Different?
Sam drew a triangle.
Dan also drew a triangle, whose angles have the same measures as the angles of Sam's triangle, and two of whose sides are equal to two of the sides of Sam's triangle.
Dan claims that both triangles must be congruent. Is Dan's claim true?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Great! From AAA, we know is the 2 triangles are similar.
However, it's still possible for them to not be congruent!
Log in to reply
But here two sides are also given equal Thus from SAS they are congruent.
Log in to reply
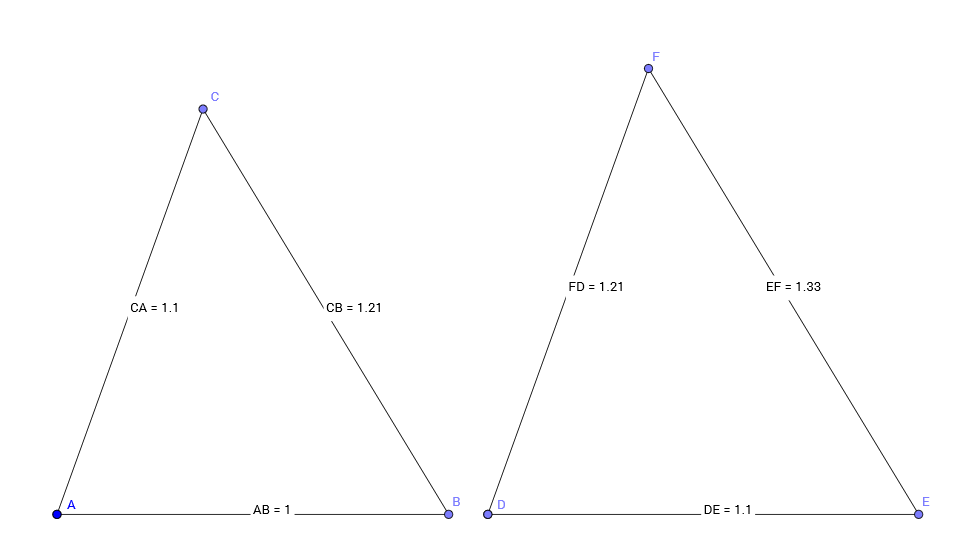
Look at his example carefully.
C A = 1 . 1 = D E and C B = 1 . 2 1 = F D
Two sides of the triangle A B C are equal to two sides of the triangle D E F but the triangles are still not congruent.
Moreover, you can't conclude that a pair of triangles are congruent from just SAS. It is just one of the necessary and sufficient conditions for them to be congruent. Two triangles that are congruent have exactly the same size and shape: all pairs of corresponding interior angles are equal in measure, and all pairs of corresponding sides have the same length.
All pairs of congruent triangles are similar; but not all pairs of similar triangles are congruent.
Log in to reply
@Kenneth Choo – Actually SAS is a condition that proves two triangles are congruent. However, SAS is not the case that is necessarily present in the problem. SAS depends on order and we do not know if the sides that are equal have the same included angle.
@Kenneth Choo – Thanks for the explanation. I thought that "a picture is worth a thousand words", but this hasn't convinced all the people.
The way I like to remember it is:
Using ASS makes an ASS out of you
IN this problem, you do not know how the angles are equal. In order to apply SAS, you need the internal angle to be the same. However, you cannot guarantee that. For example, the two triangles might be of side lengths 1 − 1 . 1 − 1 . 2 1 and 1 . 1 − 1 . 2 1 − 1 . 3 3 1 .
but in the question, we are given all angles and 2 of sides are equal, which make the two triangles congruent by ASA or even SAS
Log in to reply
We need the corresponding sides (to the angles) are equal.
IE Look at the above counterexample, which gives us an ASS case (which tends to make an ass out of people).
However, it doesn't mention that the two equal sides are corresponding sides .
A solution without decimals in sides:
sides of triangle1: 8, 12 and 18
sides of triangle2: 12, 18 and 27
Triangle2 = triangle1 * 1.5 and that mean they have the same angles.
But observe that angle 12-18 is 20.74º the smallest (of tree) in first case but is 127.17º the biggest in second case.
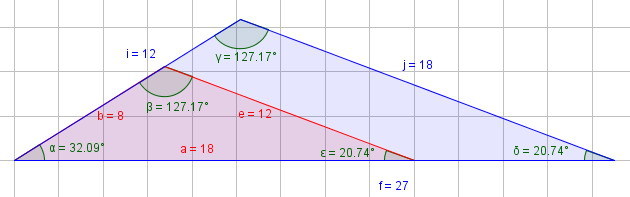
Actually, any geometrical progression {a, a r and a r^2} and {a r, a r^2 and a*r^3) with r between 1 and golden ratio (1.618...) is a solution.
Log in to reply
Good example! Most people have the misconception that this statement is always true by appyling SAS or ASA.