Tricky geometry problem
A circle passes through vertex C of a rectangle A B C D and touches its sides A B and A D at M and N respectively. If the distance from C to the line segment M N is equal to 5 units, find the area of the rectangle A B C D .
The answer is 25.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
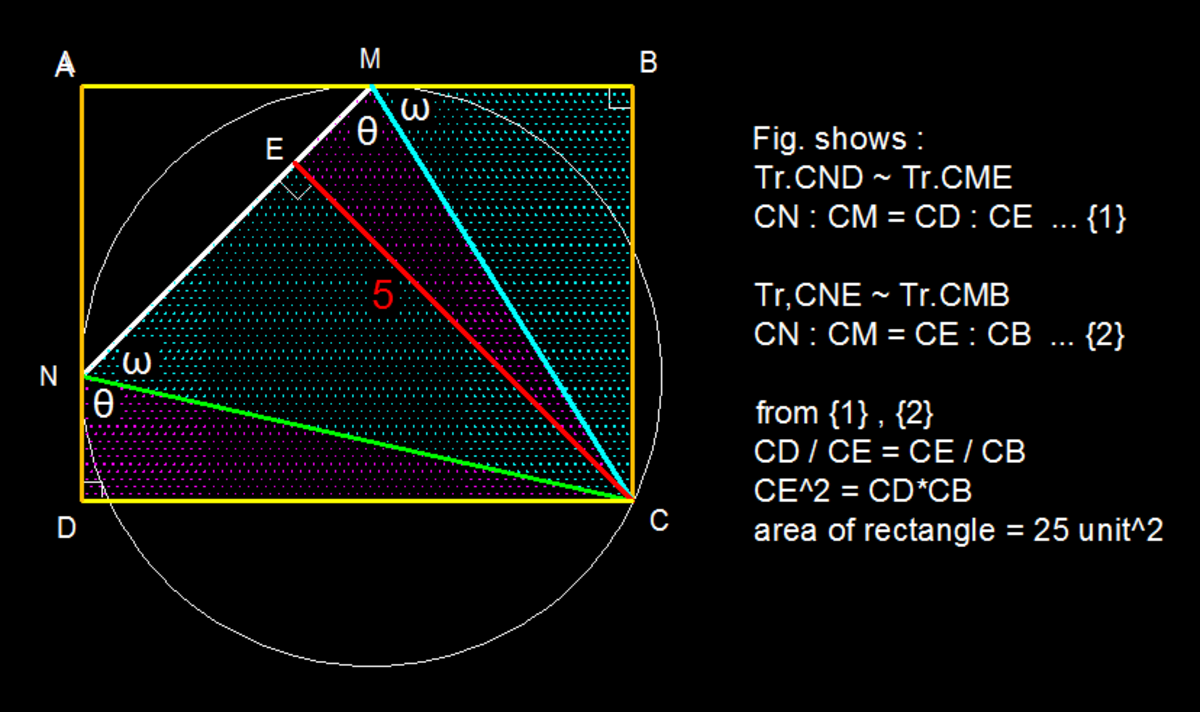
Nice solution. Up voted. You may add how tr. are similar to make it easy for some to understand..
Log in to reply
Alternate Segment Theorem
In any circle, the angle between a chord and a tangent through one of the end points of the chord is equal to the angle in the alternate segment, i.e. the angle subtended by the chord in the opposite side of the previous angle.
The same problem had appear in brilliant a few months back.
Beautiful presentation,upvoted!!
 Imgur
Imgur
Let H & W be the height and width of the rectangle ABCD. Let R and O be the radius and center of the circle. Then W = R + R cos θ ; H = R + R sin θ A r e a = A = W H = R 2 ( 1 + cos θ ) ( 1 + sin θ ) Q C = 5 = Q P + P C = 2 R + R sin α since alpha + theta = 135 degrees, 5 = 2 R + R 2 cos θ + sin θ R = 1 + cos θ + sin θ 5 2 R 2 = 2 ( 1 + cos θ ) ( 1 + sin θ ) 5 0 Substitute in the expression for area above gives
Area = 25
Hello Ujjwal, Why is QC=5?
Log in to reply
QC is given to us in the problem statement as 'distance from C to the line segment MN is equal to 5 units'
Log in to reply
Of course! Now how did I miss that?
Log in to reply
@Ajit Athle – No problem Mr Athle, happens to me all the time :-) Appreciate your interest in this solution!
Log in to reply
@Ujjwal Rane – How do you get alpha + theta = 135 degrees ?
Log in to reply
@Devendrakumar Shah – AM = AN = R; Hence line MN must be inclined at 45° with the horizontal. So QC the perpendicular to it, must be inclined at 90° + 45° = 135° with the horizontal
In 4th step after mentioning α + θ = 135°, how did you replaced sinα by sinθ +cosθ / 2 ? And "R" is also missing in that step.
Log in to reply
Thank you for noticing that missing R. I have corrected it now.
That step expresses [\alpha = 135 - \theta] while finding its sine. On expanding it, we get the result used.
Clear and simple solution as it is normal with you.