Tricky hexagon!
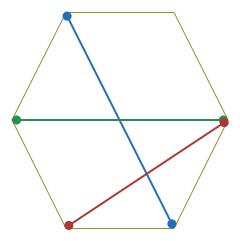 In a convex hexagon, two diagonals are drawn at random. What is the probability that the diagonals intersect
inside
the hexagon at 1 point?
In a convex hexagon, two diagonals are drawn at random. What is the probability that the diagonals intersect
inside
the hexagon at 1 point?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Discussions for this problem are now closed
...brilliant solution.(y)
Since the hexagon is convex, we know all diagonals must lie inside the polygon.
There are 9 total possible diagonals.
Of those 9 possibilities, 6 connect vertexes with one vertex between them(ie, they're sort of off to the side), and 3 connect vertexes with two vertexes between them (ie, cut the hexagon in half, if it's a regular polygon)
There is therefor a 6/9 chance that the first diagonal will be the first type, and a 3/9 chance it will be the second type
If the first diagonal is of the first type (with one point between its ends) then of the 8 remaining possible diagonals to pick, only 3 of them intersect. Thus, is 6 of 9 cases, there is a 3/8 chance of intersection.
If the first diagonal is of the second type (with two points between the ends) then of the 8 remaining possible diagonals to pick, only 4 of them intersect. Thus in 3 of 9 cases, there is a 4/8 chance of intersection.
Therefore the total probability of the second diagonal intersecting the first is:
(6/9 ) (3/8) + (3/9) (4/8) = 30/72 = 5/12
I had to draw this out, but after drawing it, we can see that there are 15 points of intersection inside the hexagon.
The number of diagonals in any convex figure is 2 n ( n − 3 ) where n is he number of sides
Thus there are 9 diagonals.
Next, we have to draw two random diagonals, thus we must do 9 choose 2
( 2 9 ) = 7 ! 2 ! 9 ! = 3 6
Thus there are 36 possible intersections.
Since 15 are inside, we have 3 6 1 5 = 1 2 5
@anyone: is there a formula for the number of intersections in a geometric figure?
Indeed there is. Theorem 1 of this paper gives I ( n ) for an n -sided regular polygon. Theorem 2 gives the number of regions R ( n ) formed. Note that this is a fairly recent paper.
Note that, for example, I ( 6 ) = 1 3 , but one of these points of intersection has multiplicity 3 , which is why we had to use a value of 1 5 in this question in order to calculate the probability.
P.S.. Your formula for the number of diagonals can be simplified to 2 n ( n − 3 ) . :)
Thanks for the simplification tip
And once again, you never cease to amaze me with your vast knowledge bank.
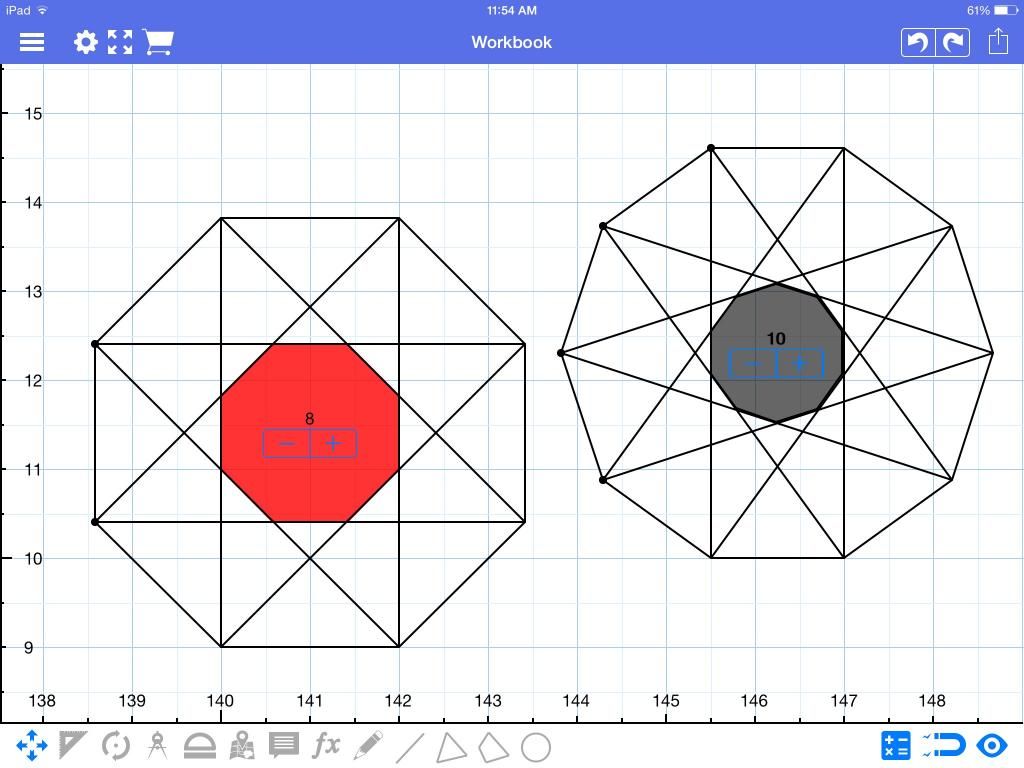
Also, is there a theorem for the area of the center section of a hexagon and octagon. Because I noticed that when the diagonals are drawn, there is a regular hexagon in the hexagon and a regular octagon in the octagon.
Hmm.... interesting observation. For the hexagon, if the side length of the primary hexagon is a then I'm getting an area of 2 3 ∗ a 2 for the interior hexagon, as it is made up of 6 identical equilateral triangles, each of height 2 a .
I'm having difficulty seeing the octagon inside the octagon; there's a lot going on in there with all the diagonals, but no interior octagons are popping out at me. :)
@Brian Charlesworth
–
 image
image
I've noticed that if the opposite diagonals are drawn for even n (number of sides) there is a smaller (regular?) polygon with the same number of sides as the reference polygon. If n is not divisible by 3, then the sides of the smaller polygon are parallel to the reference polygon. If n is divisible by three, then each side is perpendicular to at least one angle bisection.
EDIT: there is also a way to create another polygon by connecting every other vertex.
But for the polygon created by opposite diagonals, it's created by the intersection of two regular polygons with n/2 sides, so that could make it easier to find the area. (Exg: the small octagon is the intersection of 2 squares.)
@Trevor Arashiro – Ugh ...... My brain hurts...... I'm thinking of too many math problems at the same time ..... intervention needed ...... :)
@Brian Charlesworth – HAHAHAH. Too many problems, too little time, but more than enough brain power ;P
@Brian Charlesworth – For the small octagon in the octagon, I'm getting 2 s 2 2 − 2 s 2
So they have a ratio of 3 − 2 2
For the larger octagon in the octagon, I'm getting an area of 2 a 2 2 and an area ratio of 2 − 2 . Surprisingly pretty
@Trevor Arashiro – I got the same for the small octagon, but I got a 2 2 for the larger octagon, or at least the 'next size up' octagon. Is there an even bigger octagon that I'm missing?
Edit: Oh, I see which larger octagon you're referring to now. Let me check .....
Yes, the octagon one size down from the primary octagon has an area of 2 a 2 2 , as you have found.
@Brian Charlesworth – Ahh, I see which one you are referring to, I was only focusing on the octagons with sides created by the diagonals.
@Trevor Arashiro – Yeah, I was just trying to find another octagon in your drawing above without considering other diagonals.
I noticed your "Problems with diagonals" note just a moment ago. You've asked some substantial questions; it may take a while for us to chip away at them, but it's not like the polygons are going to disappear on us any time soon. :)
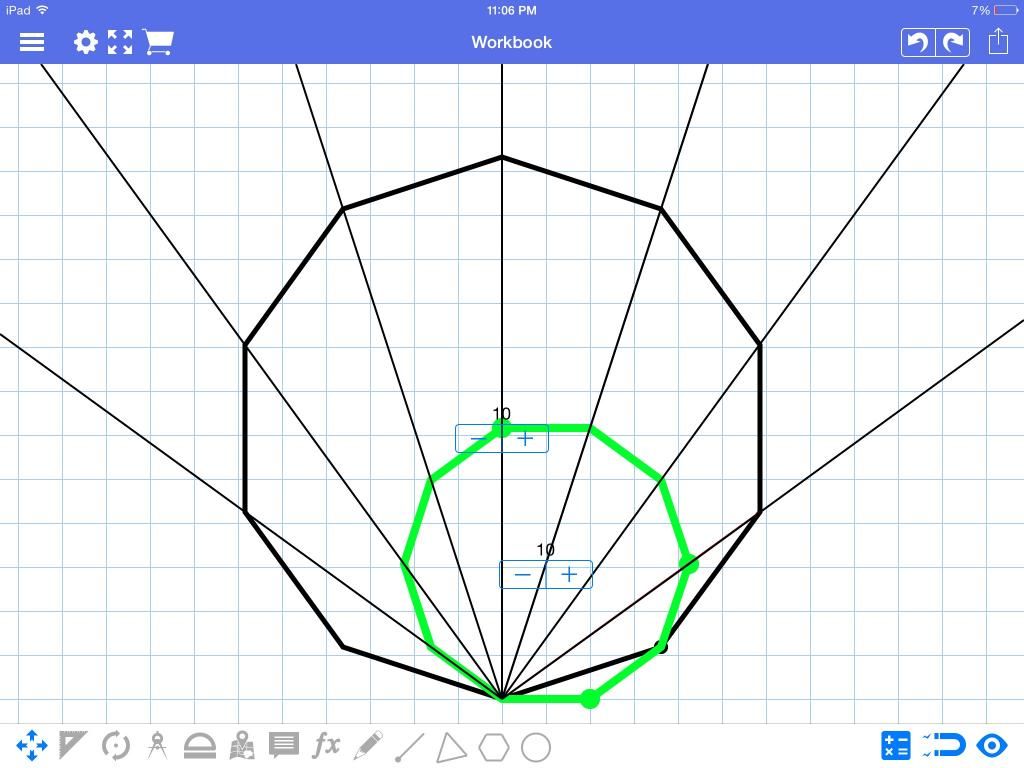
@Brian Charlesworth – I just discovered another really interesting property of polygons. If you take any vertex of an n gon, and connect it to the second closest vertex and build another n-gon off of that, all the points are co-linear.
And that's just one of 5 interesting properties I've found in under 20 mins. Is there a theorem for this?
I'll probably have to write a LONG note on this one. Gonna do most of this stuff on Sunday.
 image
image
@Trevor Arashiro – At that rate you could write a book on polygons in a week. :)
I'm not quite clear on the mechanics of how you "built" the secondary n-gon, or which points are collinear, but I'm sure you'll expand on that in your forthcoming note.
@Brian Charlesworth – Sure will. And my friend and I are actually thinking about writing a book XD
If the diagonals are formed by connecting every other point, the general formula for the ratio of the area of interior polygon to the area of the external polygon is the polynomial 1 6 x 4 + 8 x 3 − 3 1 x 2 − 8 x + 1 6 where x = cos n π . I'm still examining cases like the heptagon or octagon where there are more than one interior polygon.
@Jake Lai – Is this assuming sidelength 1?
@Trevor Arashiro – Yeah, I edited it so it would be clearer. It should be pretty easy to derive the rest by cosine rule and formulae for circumradii and apothems. The real problem is finding a general formula for the interior polygon by constructed joining every kth point.
@Jake Lai – All these problems, No time, so busy...too much school. Hahaha
nice solution
Is there any method to find the number of intersections of lines in the interior of the hexagon without drawing the figure and counting each intersection?
Total number of diagonals in hexagon = ( 2 6 ) − 6 = 9
Number of ways of selecting 2 out of 9 diagonals (Total ways) = ( 2 9 ) = 3 6
Now note that you can form a quadrilateral by selecting any 4 vertices out of 6. And each quadrilateral will have a pair of intersecting diagonals. So favorable ways = ( 4 6 ) = 1 5
Probability= 3 6 1 5 = 1 2 5
EDIT: @Trevor Arashiro You may derive formula for n-gon by this method.
Probability = ( 2 ( 2 n ) − n ) ( 4 n )