It's just 2 cut off with 2 right?
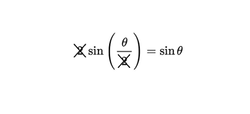 Mandy was learning trigonometric identities one day and erroneously decided that
2
sin
(
2
θ
)
=
sin
θ
was true for all
θ
. What is the sum of all values of
θ
in the interval
[
0
∘
,
3
6
0
∘
]
for which this equation is actually true?
Mandy was learning trigonometric identities one day and erroneously decided that
2
sin
(
2
θ
)
=
sin
θ
was true for all
θ
. What is the sum of all values of
θ
in the interval
[
0
∘
,
3
6
0
∘
]
for which this equation is actually true?
The answer is 360.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
2 sin 2 x = sin x
Using the principal root from the half-angle sine identity yields:
2 2 1 − cos x = sin x
Square both sides (be weary of extraneous roots!):
4 ( 2 1 − cos x ) = sin 2 x
2 ( 1 − cos x ) = 1 − cos 2 x
2 − 2 cos x = 1 − cos 2 x
cos 2 x − 2 cos x + 1 = 0
( cos x − 1 ) 2 = 0
cos x = 1
∴ x = 0 ∘ and x = 3 6 0 ∘
Checking both answers in the original equation verifies that there are no extraneous roots.
That's almost exactly how I did it! :) only on line 3 (or 4 depending how you look at it) you could use the difference of two squares to make it neater :) great solution nonetheless!
You've forgot that
sin 2 x = ± 2 1 − cos x
so
2 sin 2 x = ± 2 2 1 − cos x
and this is the reason because you've not any extraneous solutions...
Log in to reply
The negative expression produces exactly the same scenario -- after squaring -- that I outlined above (which is why I omitted it and used the principal square root). The "omission" of the negative expression has nothing to do with encountering extraneous roots.
Log in to reply
I know it... and this is the reason because the squaring doesn't produce any weird solution!
Sorry everyone, this is my first problem published, and I know absolutely no LaTeX whatsoever, if someone could try to teach me, or reformat the problem, I'd be very grateful.
It has been converted.
Don't need to apologize, everyone is a beginner at some point.
Here's a good beginner's guide to learn L A T E X : Beginner LaTeX Guide .
Can you provide a proper solution to your problem?
No problem. I think that the sum is 0 but my answer is checked as wrong. Why?
Log in to reply
You forgot 360
You basically need to reduce the problem to cos θ = 1 and sum the values after that. 0 works, but so does 360, and hence when you sum the values you get the above answer.
Log in to reply
Excuse me, but I need to reduce to
cos ( 2 θ ) = 1 because sin ( θ ) = sin ( 2 ⋅ 2 θ ) = 2 ⋅ sin 2 θ cos 2 θ
2 ⋅ sin 2 θ cos 2 θ = 2 ⋅ sin ( 2 θ ) only when cos ( 2 θ ) = 1 or when 2 ⋅ sin 2 θ = 0
The first equation has one solution in θ = 0 ° while the second one have two solutions in 2 θ = 0 ⇒ θ = 0 and 2 θ = 1 8 0 ° ⇒ θ = 3 6 0 °
So the solution 360° is right, but your hint... is wrong ;-)
Log in to reply
@Ernesto Civello – But if θ = 3 6 0 , then surely cos 2 θ gives -1, not 1. Maybe I missed something in your note, but I think you're wrong.
Log in to reply
@Elliott Macneil – Maybe I am just missing something....
Log in to reply
@Elliott Macneil – Ok. I've found my error so I try to explain:
2 sin ( 2 θ ) = sin ( θ )
2 sin ( 2 θ ) = sin ( 2 ⋅ 2 θ )
2 sin ( 2 θ ) = 2 sin ( 2 θ ) cos ( 2 θ )
a . sin ( 2 θ ) = 0 → 2 θ = 0 ° , 1 8 0 ° → θ = 0 ° , 3 6 0 °
(divide by sin ( 2 θ ) )
cos ( 2 θ ) = 1
a . 1 2 θ = 0 ° → θ = 0 ° (in contrast with the hypothesis)
a . 2 2 θ = 3 6 0 ° → θ = 7 2 0 ° (out of range)
b . sin ( 2 θ ) = 0
2 θ = 0 ° , 1 8 0 ° → θ = 0 ° , 3 6 0 ° ( O K )
0 ° + 3 6 0 ° = 3 6 0 °
Log in to reply
@Ernesto Civello – Cool, I think my solution might be different, but I totally missed your solution, it's certainly quite nice! :)
This will help you learn
L
A
T
E
X
.
http://www.codecogs.com/latex/eqneditor.php
Also, on Brilliant, when you put in the
L
A
T
E
X
commands, you need to encase them in \ ( and \ ) (without spaces in between the \ and )
Log in to reply
Thanks for the advice everyone! I'll be sure to check that site out @hobart pao, and be sure to check out my new problems, when they come out! :)
2sin(0.5x) has twice the period of sin(x). So they start together at 0 and finish at together 360. Hence sum is 0+360=360.
2sin(0.5x) would be zero at 0 and 360. But the 2"co-efficient" causes the plot to stay well above any value of sin(x), that is until it comes down to zero at 360.