Medians And Bisectors

Let the right-angle triangle be $\triangle ABC$ with $\angle BAC = \alpha$ , $\angle ABC = 90^\circ$ , $\angle DAB = \angle DAC = \dfrac{\alpha}{2}$ and $BE = EC$ , therefore, LaTeX: $\angle DAE = \theta$ .

Let $AB=1$ , then

$\begin{aligned} BC & = \tan \alpha = \frac{2\tan \frac{\alpha}{2}}{1-\tan^2 \frac{\alpha}{2}} = \frac{\frac{2}{\sqrt[3]{2}}}{1-\left(\frac{1}{\sqrt[3]{2}}\right)^2} = \frac{2^{\frac{4}{3}}}{2^{\frac{2}{3}}-1} \end{aligned}$

$\Rightarrow BE = \dfrac{BC}{2} = \dfrac{2^{\frac{1}{3}}}{2^{\frac{2}{3}}-1} \approx 2.1449$ and $BD = \tan \frac{\alpha}{2} = 2^{-\frac{1}{3}} = 0.7937$ . Since $BE > BD$ , we have $BE = \tan \left(\frac{\alpha}{2}+\theta \right)$ . Therefore,

$\begin{aligned} \tan \left(\frac{\alpha}{2}+\theta \right) & = \frac{2^{\frac{1}{3}}}{2^{\frac{2}{3}}-1} \\ \Rightarrow \frac{\tan \frac{\alpha}{2} +\tan \theta}{1-\tan \frac{\alpha}{2}\tan \theta} & = \frac{2^{\frac{1}{3}}}{2^{\frac{2}{3}}-1} \\ \frac{2^{-\frac{1}{3}} +\tan \theta}{1-2^{-\frac{1}{3}}\tan \theta} & = \frac{2^{\frac{1}{3}}}{2^{\frac{2}{3}}-1} \\ 2^{\frac{1}{3}} + 2^{\frac{2}{3}} \tan \theta - 2^{-\frac{1}{3}} -\tan \theta & = 2^{\frac{1}{3}} -\tan \theta \\ 2^{\frac{2}{3}} \tan \theta & = 2^{-\frac{1}{3}} \\ \tan \theta & = \frac{1}{2} = \boxed{0.5} \end{aligned}$

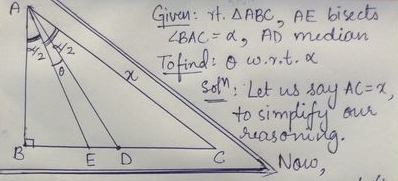
Note that here, we first found the answer for a more general problem, i.e. to express $\theta$ with respect to $\alpha$ , and then after finding the trig relation, plugged in the value of $tan\left(\dfrac{\alpha}{2}\right)$ .

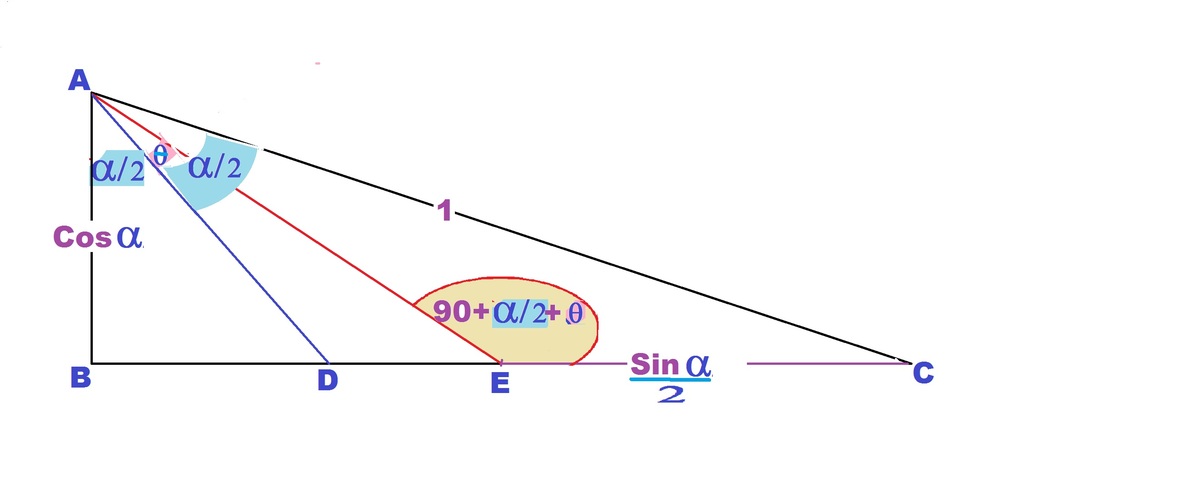
$\text{Without the loss of generality we can assume } \large~ AC=1. ~~\therefore ~AB=Cos\alpha,~~~ BC=Sin\alpha.\\ \text{Applying Sin Law to } ~~~~~~ \Delta AEC~~~~~~~~ ~\dfrac{AC}{Sin(90+\theta+\frac \alpha 2)}=\dfrac{EC}{Sin(\frac \alpha 2 - \theta)}\\ \implies~\dfrac 1 {Cos(\frac \alpha 2 + \theta)}= \dfrac{ \frac{Sin\alpha} 2 }{Sin(\frac \alpha 2 - \theta)}\\$ $\implies ~1 - Tan\frac \alpha 2 *Tan\theta= \dfrac{ 2*Tan\frac \alpha 2 } {Sin\alpha} - \dfrac 2 {Sin\alpha} *Tan\theta.\\ \implies ~Tan\theta=\large \dfrac { 1 - \dfrac{ 2*Tan\frac \alpha 2 } {Sin\alpha}} { Tan\frac \alpha 2 - \dfrac 2 {Sin\alpha}}\\ \dfrac 1{Sin\alpha}=Tan\frac{\alpha} 2+ \dfrac 1{Tan\alpha}=Tan\frac{\alpha} 2+\dfrac{1-(Tan\frac \alpha 2)^2}{2*Tan\frac \alpha 2} =\frac 1 2*Tan\frac{\alpha} 2- \dfrac 1 {2* Tan\frac{\alpha} 2}.\\ \therefore ~Tan\theta=\dfrac{ (Tan\frac{\alpha} 2)^2}{\frac 1 {Tan\frac{\alpha} 2 } }=(Tan\frac{\alpha} 2)^3=\dfrac 1 2$