Trig Minimum

$\frac{1}{\sin^2x} +\frac{1}{\cos^2x} = \frac{\sin^2x +\cos^2x}{\sin^2x \cos^2x}\\ = \frac{1}{\sin^2x \cos^2x}\\ \text{The minimum value of this expression is 4 at} \,x= \frac{\pi}{4}$

$­(sin^{-1} \ ­x)^{2}+(cos^{-1} \ x­)^{2}=$ $­ ( \frac{1}{sin \ ­x})^{2}+( \frac{1}{cos \ ­x})^{2}=$

$­ ( \frac{cos^{2} \ ­x}{sin^{2} \ ­x \ . \ cos^{2} \ ­x})+( \frac{sen^{2} \ ­x}{sin^{2} \ ­x \ . \ cos^{2} \ ­x})=$ $­( \frac{1}{sin^{2} \ ­x \ . \ cos^{2} \ ­x})=$ $­( \frac{4}{4 \ . \ sin^{2} \ ­x \ . \ cos^{2} \ ­x})=$

$\ [ \frac{4}{(2 \ . \ sin \ ­x \ . \ cos \ ­x)^{2}} \ ] =$ $\frac{4}{sIn^{2} \ ­2x} =$ ${4 \ . \ cosec^{2} \ ­2x}$

The $cosec \ n$ function has positive and negative values. When in negative range, its local maxima values are $-1$ , and when in positive range, its local minima values are $1$ .

$cosec \ n$ function

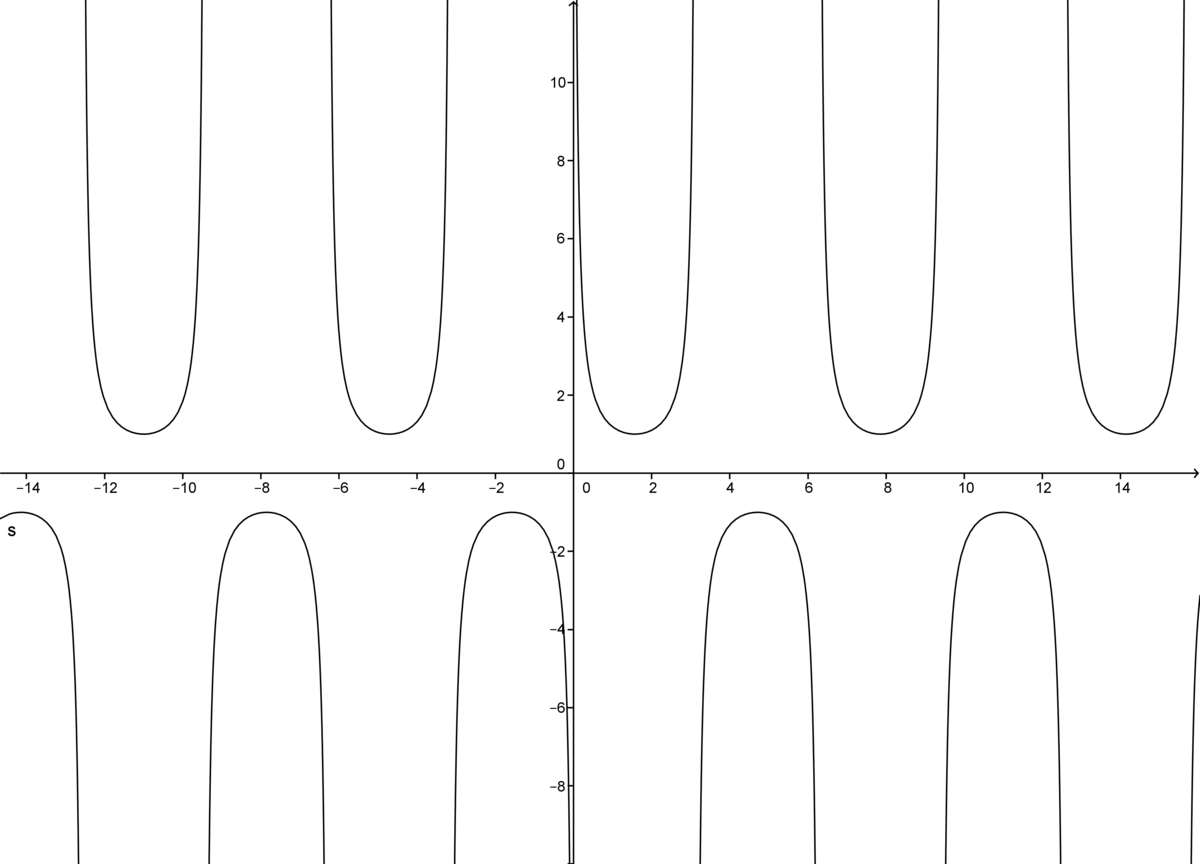
$cosec^{2} \ n$ function

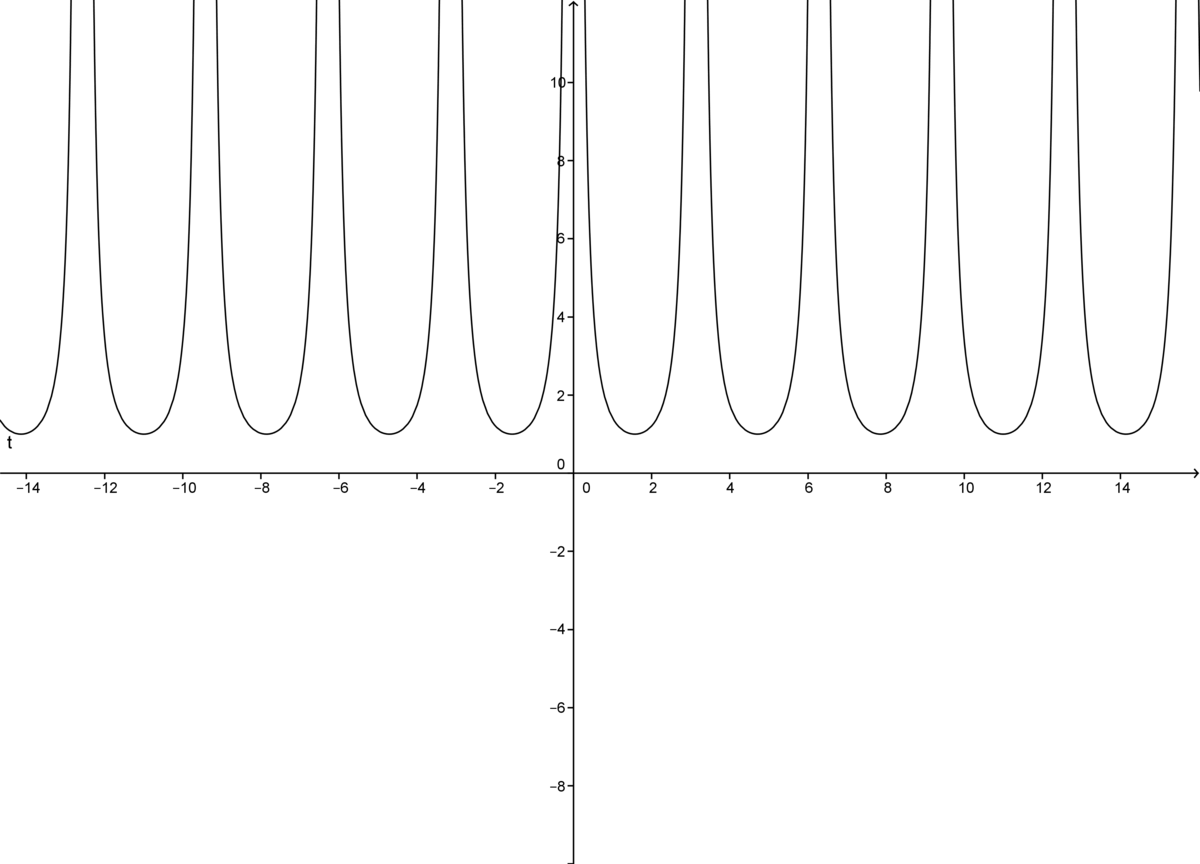
Thus, and taking a glance at the $cosec \ n$ and $cosec^{2} \ n$ functions above, we get that the composite ${4 \ . \ cosec^{2} \ ­2x}$ function has $4$ as minima values. This occur at ${4 \ . \ cosec^{2} \ ­2x}=4 \rightarrow cosec^{2} \ ­2x=1 \rightarrow cosec \ ­2x= \pm \sqrt{1} \rightarrow$

$\rightarrow x \in \{ \frac{\pi}{4}, \ \frac{3 \pi}{4}, \ \frac{5 \pi}{4}, \ \frac{7 \pi}{4} \}$ , for $x \in \ [ 0,\ 2 \pi \ [$ . Hence, the answer is $\boxed{\frac{\pi}{4}}$ .

${4.cosec^{2} \ ­2x}$ function