Tricky Trig
sin θ + cos θ = 2 sin ( 9 0 ∘ − θ ) , cot θ = ?
Give your answer to the above problem to 3 decimal places.
The answer is 2.414.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
12 solutions
Thank you :)
How can you divide by a variable? what if cos x is 0?
Log in to reply
You can easily prove that cos x = 0 . Let's say if otherwise cos x = 0 , substitute it into the original equation you get sin x = 0 , however sin 2 x + cos 2 x = 0 = 1 , this is a contradiction. So cos x = 0 .
Whats wrong here ? Sin(x)cos(45) + cos(x)sin(45) =sin(90-x) Sin(45+x)=sin(90-x) Or 2x=45 X=45/2 Cot(45/2)= 1.7926
Done with same approach.. Best of luck :)
Looks easy but when you tries to solve, it becomes hard!!! but once again it becomes easy when you looks at the solution!!!
I got the right ans. i.e sqrt2 +1. But i approxed it to 2.41 just two decimal places and its says your ans. Is incorrect. Wth.
sin θ + cos θ = 2 sin ( 9 0 ° − θ )
sin θ + cos θ = 2 cos θ
sin θ = ( 2 − 1 ) cos θ
2 − 1 1 = sin θ cos θ
1 2 + 1 = cot θ
= > cot θ = 1 . 4 1 4 . . . + 1
cot θ ≈ 2 . 4 1 4
sin x + cos x=2^1/2 sin (90-x)
because of sin (90-x)= cos x,
sin x + cos x=2^1/2 cos x
dividing terms with sin x,
sin x/sin x + cos x/sin x=2^1/2 cos x/sin x
1+cot x=2^1/2 cot x
1= (2^1/2-1) cot x
cot x =2.41
Whats wrong here ? Sin(x)cos(45) + cos(x)sin(45) =sin(90-x) Sin(45+x)=sin(90-x) Or 2x=45 X=45/2 Cot(45/2)= 1.7926
Log in to reply
What's wrong is that you can't jump from sin ( 4 5 ∘ + x ) = sin ( 9 0 ∘ − x ) to 4 5 ∘ + x = 9 0 ∘ − x .
Log in to reply
so whats the right step after that ? please tell me ! thanks !
Log in to reply
@Purushottam Gupta – From there, you could take sin ( 9 0 ∘ − x ) to the RHS and simplify, but I don't see any efficient method from there.
Whats wrong here ? Sin(x)cos(45) + cos(x)sin(45) =sin(90-x) Sin(45+x)=sin(90-x) Or 2x=45 X=45/2 Cot(45/2)= 1.7926
Given ,
sin x + cos x = root(2) sin (90 - x) = root(2) cos x
sin x = root(2) cos x - cos x
Taking out cos x common from the RHS we get ,
sin x = cos x ( root(2) - 1)
sin x / cos x = root(2) - 1
tan x = 0.4142
cot x = 1 / 0.4142 = 2.414
Hence the value of cot x is 2.414 upto three decimal places.
Easy question if you have absolutely read trigonometry.
s i n θ + c o s θ = 2 c o s θ Dividing by s i n θ we get, 1 + c o t θ = 2 c o t θ Simplifying yields, c o t θ = 2 − 1 1
Does this question require a solution? It's too easy. No offence
sinx + cosx = sqrt(2)cosx
sinx={sqrt(2)-1}cosx
cosx/sinx=1/{sqrt(2)-1}
cotx=sqrt(2) + 1
So, cotx=2.414
Using r-formula, sinX + cosX = sqrt(2)sin(X + 45deg)
X + 45deg = 90deg - X
Thus one possible value of X is 67.5deg
Unfortunately, I got stuck here and had to use the calculator to find cot(67.5deg).
Esy.... sinx+cosx=2^1/2sin(90_x) =sinx+cosx=2^1/2cosx =sinx=(2^1/2-1)cosx =tanx=2^1/2-1 =cotx=2^1/2+1 =cotx=2.414 (approx)
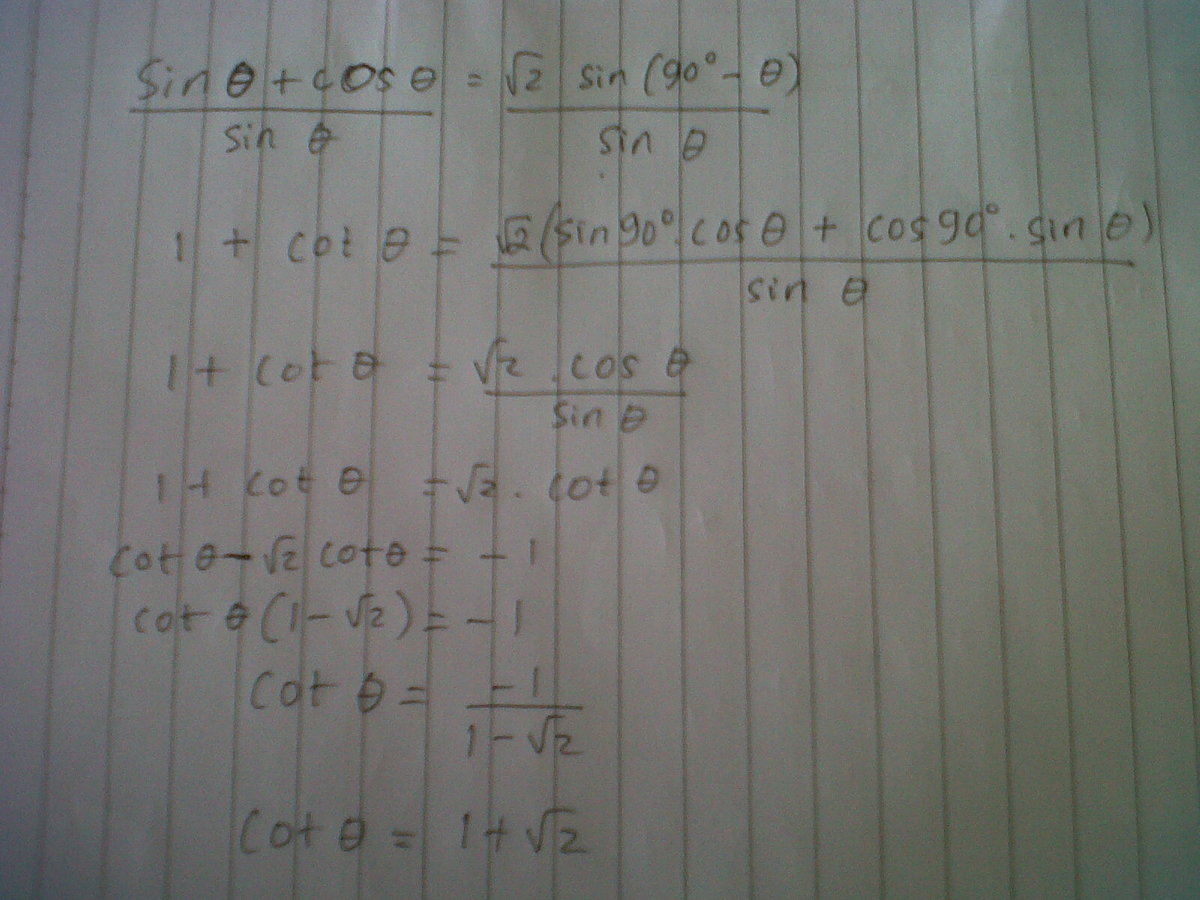


sin ( 9 0 − x ) = cos ( x )
Using this identity
sin ( x ) + cos ( x ) = 2 cos ( x )
cos ( x ) sin ( x ) + cos ( x ) = 2
cos ( x ) sin ( x ) + cos ( x ) cos ( x ) = 2
Remember
cos ( x ) sin ( x ) = tan ( x )
∴ tan ( x ) + 1 = 2
tan ( x ) = 2 − 1
cot ( x ) = 2 − 1 1 ≈ 2 . 4 1 4