Trigonometry
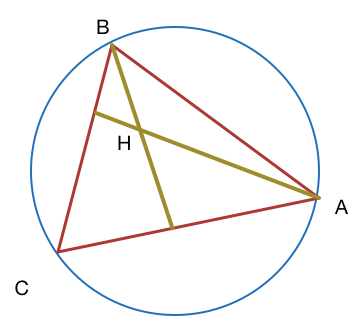 Δ
A
B
C
is inscribed in a circle of radius
5
.
H
is the orthocentre of
Δ
A
B
C
. If
tan
A
=
1
,
tan
B
=
2
then find
C
H
2
.
Δ
A
B
C
is inscribed in a circle of radius
5
.
H
is the orthocentre of
Δ
A
B
C
. If
tan
A
=
1
,
tan
B
=
2
then find
C
H
2
.
This problem is part of the set Trigonometry .
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
@Omkar Kulkarni I added an image to your problem. Can you check that it is correct?
Log in to reply
Yeah, it is. Btw could you tell me from where you make these images? I wanna do the same.
Log in to reply
If you just want geometric diagrams, I suggest using Geogebra.
I use a program called OmniGraffle, because I typically need more flexibility, like shading regions or having cubic splines.
OMG! We solved using the exact same method! High five!
Can anyone help me to understand this relation C H = 2 R cos C ?
Log in to reply
Yes! Actually you can prove it! Wait for today, I'll post in the evening... :)
You got it? Just use Sine Rule as well as basic trigonometric relations to get the answer...
Log in to reply
No, I still didn't get it... I've tried to use Sine Rule or Cosine Rule, but I can't find a relation with CH and cos C...
Log in to reply
@Ricardo Takayama – Let D be the point of intersection of A H and B C . So, C D = A C ∘ cos C = b cos C and also C H D = B . So , C H = sin B C D = sin B b cos C = 2 R cos C
Log in to reply
@Kishore S. Shenoy
–
Thanks, Kishore S Shenoy , I get it all until that step. It is still difficult for me to see, thanks for taking the time. It looks like you are stating
sin
B
b
=
2
R
My work below yields this to be true, b ~ 8.9 and sin 63.4 ~ .89 so the ratio = 10.
But how do you interject the 2R in there?
Log in to reply
@Ken Hodson – Interject 2 R ??
@Ken Hodson – tan A = 1 => A = 4 5 º => a = 2 R
By Sine Rule: sin B b = sin A a = sin 4 5 º 2 R = 2 R
Log in to reply
@Ricardo Takayama – Don't use like this. Use the Extended Sine Rule ! sin A a = sin B b = sin C c = 2 R
@Kishore S. Shenoy – Thank you very much! I've spent a lot of time trying to understand this problem. I hadn't seen that C H D = B . And now I've realized where you use the Sine Rule, in the last step.
@Ricardo Takayama – I wouldn't spend too much time on it. The solution is flawed. As is the original problem.
Log in to reply
@Ken Hodson – It is not flawed. The answer is correct
Log in to reply
@Kishore S. Shenoy – Can someone write out a detailed solution then? I'm with @Ricardo Takayama. I don't see the logic in the top solution, as too many steps are missed. Further, I've written a lengthy response where I identify almost every angle and line segment. I find that C'H^2 is indeed 10, but not CH^2.
Log in to reply
@Ken Hodson – Wait, I'm posting a comment.
This would probably a result of investigation as specific answer or knowledge to this question if it is indeed correct. Not a fundamental derivation, I think.
This one is frustrating. I used a lot of trig and still got it wrong. But I can't find my error. If anyone cares to look at my work, and show me where I went astray. To assist, consider points A', B' and C' which are the unnamed points where the altitudes intersect their opposite sides. A' lies on B C etc.
Since the TAN of A, or better the TAN of ∠ B A C = 1 , ∠ B A C = 4 5 .
Further, BC would = \(5\sqrt2 \ = 7.1) This is because the arc it cuts is 90 degrees, and the radius is 5. There's some undrawn triangle BCO that is a right isosceles triangle, and BC is the hypotenuse.
If TAN of \( \angle ABC = 2, \angle ABC = 63.4 \)
Then ∠ B C A = 7 1 . 6
The altitude BB' is the sin 71.56 = x/7.1 ; x= 6.7 And triangle BB'A is a right isosceles triangle so B'A is 6.7.
Without showing anymore math (it was all , I'll list out my dims.
AB = 9.5
a n g l e B A A ′ = 2 6 . 6
a n g l e H A C = 4 5 − 2 6 . 6 = 1 8 . 4
a n g l e C B H = 1 8 . 4
These two 18.4 degree angles were key and since earlier I found B'A = 6.7, for Triangle HAB'
HB' = 4.1
And since earlier I found BC = 7.1
for Triangle BB'C,
CB' = 2.2
And the answer I got CH is the hypotenuse of right triangle CB'H and is 4.65 or
4
.
6
5
2
=
2
1
.
6
My work yields that C ′ H 2 i s 1 0 , but not C H 2 C H 2 i s 2 1 . 6 .
I think both the question, and this solution contain an error. As
@Sauvik Mondal
's work pointed out at the bottom of the page,
@Michael Ng
's answer is for C'H^2, not CH^2.
Further, the original problem can't be answered correctly, because CH^2 is not an integer.
I would rather think that C H = 2 R cos C is a specific knowledge than a general basic.
suppose O is the circumcenter.then <BOC=2<BAC.now tan<BAC=1 implies <A=45.Let extended CH cuts AB at C' and BH cuts AC at B'.Now HC'=BC'(=x) and HB'=CB'(=y).Now tan<B=2 implies (\sqrt { 2 } y+x)/x=2,or \sqrt { 2 } y=x.It's a well known fact that AH=2.OS(S is the feoot of the perpendicular from O to BC.But \sqrt { 2 }.OS=5.Using pythagoras theorem on triangle AC'H we get (x+\sqrt { 2 }.y)^2+x^2=50 we get 2.y^2=10
I'm glad you posted this. This means my answer up there isn't wrong. The top solution, that CH^2 = 10 is incorrect. C'H^2 = 10, but not CH^2.
tanA = 1, So, A = 45
tanB = 2, So, B = atan(2) = 63.434
C = 180 - (A+B) = 180-108.434 = 71.565
CH = 2R cos C
= 2 * 5 * cos(71.565)
= 10*0.3162
= 3.1622
CH^2 = 3.1622^2 = 10.
from tan(A)=1 and tan(B)=2, we know that: sin(A)=1/sqrt(2), sin(B)=2/sqrt(5), sin(C)=3/sqrt(10)
a/sin(A)=b/sin(B)=c/sin(C)=2R=10, with a, b and c the lengths of the sides of the triangle, this gives: a=5 sqrt(2), b=4 sqrt(5), c=3 sqrt(10)
Define a catresian system so that (keep in mind that the angle in A is pi/4 or 45°): A=(0, 0, 0), B=(3 sqrt(10), 0), C=(2 sqrt(10),2 sqrt(10))
orthocentre through A is given by y=x/2
orthocentre through C is given by x=2 sqrt(10)
Coördinates of H, on the intersection of these two lines, are therefore (2 sqrt(10), sqrt(10))
d(C,H)=2 sqrt(10) - sqrt(10) = sqrt(10) or CH² = 10
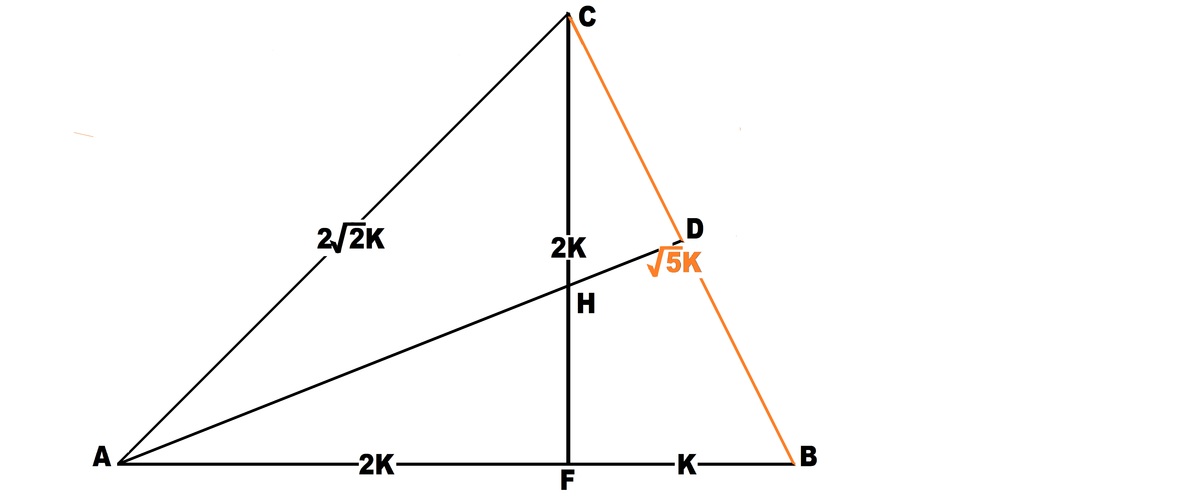 D and F are the feet of the altitudes of triangle ABC as shown on the sketch.
Let AB=3k where k is the scale factor. Since
A
=
T
a
n
−
1
1
a
n
d
B
=
T
a
n
−
1
2
,
∴
A
F
=
2
k
,
F
B
=
k
,
C
F
=
2
k
.
A
p
p
l
y
i
n
g
P
y
t
h
a
g
o
r
a
s
t
o
Δ
s
C
A
F
a
n
d
C
F
B
,
C
A
=
2
∗
2
∗
k
,
C
B
=
5
k
.
A
p
p
l
y
i
n
g
E
x
t
e
n
d
e
d
S
i
n
L
a
w
t
o
Δ
A
B
C
,
2
∗
R
=
1
0
=
S
i
n
A
C
B
=
5
k
∗
2
.
⟹
k
=
1
0
.
I
n
t
h
e
r
t
.
∠
e
d
Δ
s
C
A
D
a
n
d
C
H
D
,
C
A
∗
C
o
s
C
=
C
D
=
H
C
∗
S
i
n
B
,
∴
H
C
=
S
i
n
B
C
A
∗
C
o
s
(
1
8
0
−
A
−
B
)
=
S
i
n
B
2
∗
2
∗
1
0
∗
C
o
s
(
1
8
0
−
A
−
B
)
.
⟹
H
C
2
=
1
0
D and F are the feet of the altitudes of triangle ABC as shown on the sketch.
Let AB=3k where k is the scale factor. Since
A
=
T
a
n
−
1
1
a
n
d
B
=
T
a
n
−
1
2
,
∴
A
F
=
2
k
,
F
B
=
k
,
C
F
=
2
k
.
A
p
p
l
y
i
n
g
P
y
t
h
a
g
o
r
a
s
t
o
Δ
s
C
A
F
a
n
d
C
F
B
,
C
A
=
2
∗
2
∗
k
,
C
B
=
5
k
.
A
p
p
l
y
i
n
g
E
x
t
e
n
d
e
d
S
i
n
L
a
w
t
o
Δ
A
B
C
,
2
∗
R
=
1
0
=
S
i
n
A
C
B
=
5
k
∗
2
.
⟹
k
=
1
0
.
I
n
t
h
e
r
t
.
∠
e
d
Δ
s
C
A
D
a
n
d
C
H
D
,
C
A
∗
C
o
s
C
=
C
D
=
H
C
∗
S
i
n
B
,
∴
H
C
=
S
i
n
B
C
A
∗
C
o
s
(
1
8
0
−
A
−
B
)
=
S
i
n
B
2
∗
2
∗
1
0
∗
C
o
s
(
1
8
0
−
A
−
B
)
.
⟹
H
C
2
=
1
0
Note:- angle A=arcTan1=45, angle B=arcTan2=63.4349.
I think everybody is using own way for this question. Therefore, I should also tell how I did this.
Start from the end, let me write about the last steps first. Assign A as origin.
We shall obtain A (0, 0), B ( 3 1 0 , 0) and C (2 1 0 , 2 1 0 ). Solve by geometry:
x − 3 1 0 y − 0 = 2 1 0 − 3 1 0 2 1 0 − 0 = − 1 0 2 1 0 = -2 is the line B C.
Perpendicular line to B C from A (0, 0) crossing it should have a gradient of 2 1 for m 1 m 2 = -1.
Therefore, this line y = 2 1 x is intercepting with the line of C (2 1 0 , 2 1 0 ) to the x-axis.
At x = 2 1 0 , y = 1 0 . This is point H.
Obviously, for C H parallel to the y-axis, C H = 2 1 0 - 1 0 = 1 0 .
Therefore ( C H ) 2 = ( 1 0 ) 2 = 10.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
R e s o u r c e s :
Given that tan A = 1 and tan B = 2,
tan C = tan (180 ∘ - A - B) = - tan (A + B) = - 1 − t a n A t a n B t a n A + t a n B = 3.
s i n 2 x = 1 + t a n 2 x 2 t a n x
sin 2 A = 1 and sin A = 2 1
sin 2 B = 5 4 and sin B = 5 2
sin 2 C = 5 3 and sin C = 1 0 3
a b 1 0 3 = b c 2 1 = a c 5 2 = a h a = b h b = c h c = 5 2 (1 + 5 4 + 5 3 ) = 60
Therefore,
a = 5 2 and h a = 6 2
b = 4 5 and h b = 3 5
c = 3 1 0 and h c = 2 1 0
∠ A = 45 ∘ makes coordinates of C an ease to determine.
b = AC = 4 5
⟹ A C ′ = 2 A C = 2 1 0 ,
Therefore, C is located at ( 2 1 0 , 2 1 0 ).
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
This solution takes n o special theorem as resources for answering the question.
Answer: 1 0
Since other solutions have been taken, we will use barycentric coordinates.
From the relation tan A + tan B + tan C = tan A tan B tan C we find tan C = 3 .
Thus, H = ( tan A : tan B : tan C ) = ( 1 : 2 : 3 ) = ( 6 1 , 3 1 , 2 1 )
This implies that C H ∣ C H ∣ 2 = ( 6 1 , 3 1 , − 2 1 ) = − a 2 y z − b 2 x z − c 2 x y = 6 a 2 + 1 2 b 2 − 1 8 c 2
However, will tan , we can derive sin and the side lengths easily. a b c = 2 R sin A = 5 2 = 2 R sin B = 4 5 = 2 R sin C = 3 1 0 Substituting these values, we get that C H 2 = 1 0 .
Using trigonometry we can derive that C H = 2 R cos C so C H 2 = 4 R 2 cos 2 C . Now A + B + C = 1 8 0 ∘ so:
tan A + tan B + tan C = tan A tan B tan C
then substituting in and solving gives tan C = 3 . Therefore sec 2 C = tan 2 C + 1 = 1 0 ⟹ cos 2 C = 1 0 1 .
Therefore C H 2 = 4 × 5 2 × 1 0 1 = 1 0 .