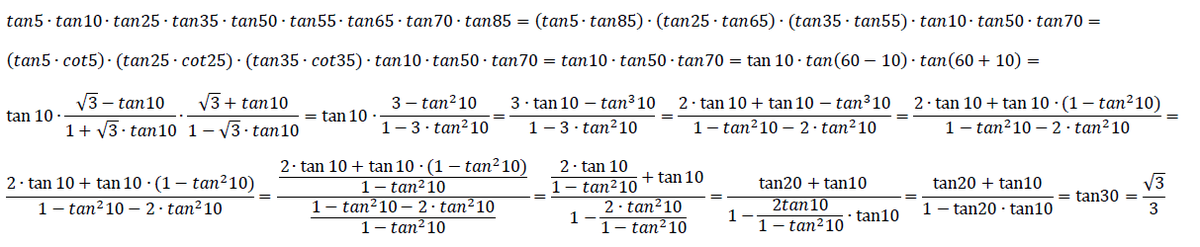Random Assortment of $\tan x$

Geometry Level 3

$\tan5^\circ \tan10^\circ \tan25^\circ \tan35^\circ \tan50^\circ \tan55^\circ \tan65^\circ \tan70^\circ \tan85^\circ = \, ?$

\frac1{\sqrt3}

\sqrt3

2 solutions

Raj Rajput
Jan 26, 2016

Nice solution. I made it more complicated than necessary by using the identity $\tan(x)\tan(60 - x)\tan(60 + x) = \tan(3x)$ , (in degree measure), on three sets of three terms, namely

$\tan(5)\tan(55)\tan(65) = \tan(15), \tan(10)\tan(50)\tan(70) = \tan(30)$ and

$\tan(25)\tan(35)\tan(85) = \tan(75)$ .

The resulting product is then $\tan(30)\tan(15)\tan(75) = \tan(30)$ ,

since $\tan(15)\tan(75) = \tan(15)\cot(15) = 1$ .

Brian Charlesworth - 5 years, 4 months ago

$\tan(25)\tan(35)\tan(\color{#D61F06}{80})=\tan(75)$

$\color{#3D99F6}{???85???} \quad$ $\Huge{\ddot \smile}$

$\scriptsize \text{Because in the last line,} \tan(\theta)\times\tan(\frac{\pi}{2}-\theta)=1$

Cleres Cupertino - 5 years, 4 months ago

Edit made; thanks for catching that typo. :)

Brian Charlesworth - 5 years, 4 months ago

"tan(30)tan(15)tan(75)" how the product of this term is equal to "tan(30)"? its not following the tan(x)tan(60-x)tan(60+x)=tan(3x) formula.

Madhumish Sn - 5 years, 4 months ago

$\text{Realize that,} \quad \boxed{\tan(\theta)\times\tan(\frac{\pi}{2}-\theta)=1}$

Cleres Cupertino - 5 years, 4 months ago

@Cleres Cupertino – Thank you :)

Madhumish Sn - 5 years, 4 months ago

because tan(75)=cot(15) and tan(15)xcot(15) = 1

RAJ RAJPUT - 5 years, 4 months ago

Κώστας Σιώπης
Feb 1, 2016

Random Assortment of tan ⁡ x \tan x tan x

2 solutions

0 pending reports

Random Assortment of $\tan x$