Triple Polynomial Equation

Let $f(x)=\sum_{m=0}^n a_m x^m.$

The degrees of both $f(x^3)$ and $f(x^3-2)$ are $3n$ . Since their head-coefficients are both $a_n$ and they only have terms of the form $cx^{3m}$ , the degree of $f(x^3)-f(x^3-2)$ is at most $3(n-1)$ . The degree of $(f(x))^2$ is $2n$ .

So for the degree $n$ of $f(x)$ goes $3(n-1)=2n$ , so $n=3$ .

Let $f(x)=a_0+a_1x+a_2x^2+a_3x^3.$ $f(x^3)-f(x^3-2)=(f(x))^2+12$ $\Leftrightarrow (a_0+a_1x^3+a_2x^6+a_3x^9)-(a_0+a_1(x^3-2)+a_2(x^3-2)^2+a_3(x^3-2)^3)=(a_0+a_1x+a_2x^2+a_3x^3)^2+12$ $\Leftrightarrow (2a_1-4a_2+8a_3+4a_2x^3-12a_3x^3+6a_3x^6=a_0^2+12+2a_0a_1x+(2a_0a_2+a_1^2)x^2+(2a_0a_3+2a_1a_2)x^3+(2a_1a_3+a_2^2)x^4+2a_2a_3x^5+a_3^2x^6$

Which gives us: $6a_3=a_3^2$ , so $a_3=6.$

And $0=2a_2 \times 6$ , so $a_2=0$ .

And $0=2a_1 \times 6 + 0^2$ , so $a_1=0$ .

And finally $2 \times 0-4 \times 0+8 \times 6 = a_0^2+12$ , so $a_0=-6$ .

This gives us $f(x)=-6+6x^3.$

So $f(5)=-6+6 \times 5^3 = \fbox{744}.$

Let the degree of $f(x)$ be $n$ . Observe that the degree of the LHS is $3(n-1)$ and the degree of the RHS is $2n$ . These have to be equal, thus $3n-3=2n\Rightarrow n=3$ . If we let $f(x)=ax^3+bx^2+cx+d$ , we can substitute this into the equation. After we expand everything, we see that the coefficients of the $x^6$ terms have to match. This implies $a^2=6a$ , so $a=0$ or $a=6$ . The former will cause $f(x)$ to be constant, so $a$ must be $6$ . Because the LHS does not have an $x^5$ term, $ab=0\Rightarrow b=0$ . Similarly, we have $ac=0\Rightarrow c=0$ . Looking at the terms with degree $3$ , we have $2ad=12a\Rightarrow d=6$ . We can plug these values into the equation to see that everything works out. Therefore, $f(x)=6x^3-6$ and $f(5)=744$ .

Let $f(x) = a_0 + a_1x + a_2x^2 + ... + a_nx^n$ . All terms on the left side of the equation have powers of $x$ divisible by $3$ , so the same should hold for the right side. $a_i \neq 0 \Rightarrow i \equiv 0 \mod 3$ [How would you show this? - Calvin]

Let's consider the degrees on both sides. On the LHS, the $x^{3n}$ term cancels out and the $x^{3n-3}$ terms are $a_{n-3}x^{3n-3} - \left( a_{n-3}x^{3n-3} - a_nx^{3n-3}2^3\binom{n}{3} \right)$ , which is non-zero, so the degree is $3n-3$ [Note: Do you see how we used the fact that the polynomial is not constant in this step?]. The degree of the RHS is $2n$ , so we must have $3n-3 = 2n \Rightarrow n=3$ . Now by simply substituting $f(x) = ax^3 + b$ we get $f(x) = 6x^3 - 6$ , and $f(5) = 744$ .

[Edits for clarity - Calvin]

Let the degree of $f(x)$ be denoted $n$ . I claim that the degree of $f(x^3)-f(x^3-2)$ is $3n-3$ . The proof is as follows:

Let $f(x)=a_n x^n+a_{n-1}x^{n-1}+\cdots+a_1x+a_0$ . Then $f(x^3)=a_nx^{3n}+a_{n-1}x^{3n-3}+\cdots+a_1x+a_0$ and $f(x^3-2)=a_n(x^3-2)^n+a_{n-1}(x^3-2)^{n-1}+\cdots+a_1(x^3-2)+a_0$ . Clearly, the leading term of both polynomials is $a_nx^{3n}$ and cancel when we perform the subtraction $f(x^3)-f(x^3-2)$ . Furthermore, the coefficient of the $x^{3n-3}$ term in $f(x^3)$ is $a_{n-1}$ , while with the help of the Binomial Theorem we see that the coefficient of the $x^{3n-3}$ term in $f(x^3-2)$ is $a_n\left[-2\binom{n}{1}\right]+a_{n-1}$ . Because $a_n$ is nonzero, this is not equal to $a_{n-1}$ , so $f(x^3)-f(x^3-2)$ is indeed of degree $3n-3$ , as claimed.

Having established that the polynomial on the left side of the given equation is of degree $3n-3$ , we note further that the right hand side polynomial is of degree $2n$ . This gives us the equation $3n-3=2n$ , from which we deduce $n=3$ . Hence we can write $f(x)=ax^3+bx^2+cx+d$ for some $a, b, c, d$ . It follows that

$f(x^3)=a(x^3)^3+b(x^3)^2+c(x^3)+d=ax^9+bx^6+cx^3+d$

and

$f(x^3-2)=a(x^3-2)^3+b(x^3-2)^2+c(x^3-2)+d$ $=ax^9+(b-6a)x^6+(12a-4b+c)x^3-8a+4b-2c+d$ .

Thus,

$f(x^3)-f(x^3-2)=6ax^6+(4b-12a)x^3+8a+2c-4b$

We also have

$(f(x))^2+12=(ax^3+bx^2+cx+d)^2+12$ $=a^2x^6+2abx^5+(b^2+2ac)x^4$ $+(2ad+2bc)x^3+(c^2+2bd)x^2+2cdx+d^2+12$ .

(I have omitted all the trivial computation.) We are now ready to equate the two expressions. Equating the coefficients to each other, we get $a^2=6a, 2ab=0, b^2+2ac=0, 2ad+2bc=4b-12a$ $, c^2+2bd = 0, 2cd = 0, d^2+12=8a+2c-4b$ . It is then easy to solve this system of equations to find that $(a, b, c, d)=(6, 0, 0, -6)$ . Hence, $f(x)=6x^3-6$ , and the requested answer is $f(5)=6(5^3)-6=\boxed{744}$ .

First, let's determine the degree of polynomial $f(x)$ . Suppose it's n. So, on the left side of the equation, the greatest degree that will appear is $3(n-1)=3n-3$ (because the degree $3n$ will be canceled), and the greatest degree on the right side is $2n$ . So, $3n-3=2n\Longrightarrow n=3$ , the degree of polynomial $f(x)$ is $3$ . Let $f(x)=ax^3+bx^2+cx+d$ :

$f(x^3)=ax^9-bx^6+cx^3+d$

$f(x^3-2)=a(x^3-2)^x+b(x^3-2)^2+c(x^3-2)+d$ $=ax^9-6ax^6+12ax^3-8a+bx^6-4bx^3+4b+cx^3-2c+d$

So,

$f(x^3)-f(x^3-2)=6ax^6+x^3(-12a+4b)+(8a-4b+2c)$

$(f(x))^2= (ax^3+bx^2+cx+d)^2$ $=a^2x^6+2abx^5+x^4(b^2+2ac)+x^3(2ad+2bc)+x^2(c^2+2bd)+2cdx+(d^2+12)$

So, we have:

$6ax^6+x^3(-12a+4b)+(8a-4b+2c)=$ $a^2x^6+2abx^5+x^4(b^2+2ac)+x^3(2ad+2bc)+x^2(c^2+2bd)+2cdx+(d^2+12)$

They are equal if, and only if, the factor of the same degree are equal, so:

$6a=a^2\Longrightarrow a=6$ (the factor of $x^6$ ).

$2ab=0\Longrightarrow b=0$ (the factor of $x^5$ ).

$b^2+2ac=0\Longrightarrow c=0$ (the factor of $x^4$ ).

$2ad+2bc=-12a+4b\Longrightarrow 12d=-72\Longrightarrow d=-6$ (the factor of $x^3$ ).

So, we have:

$f(x)=6x^3-6$ .

So, $f(5)=6\cdot5^3-6=744$ .

$f(x)$ is given to b a polynomial of degree $n\geq 1$ . On the L.H.S we have $x^3$ being plugged in to the polynomial, giving a polynomial of degree $3n$ and then $x^3-2$ is plugged in and subtracted. Since the terms of degree $3n$ have the same leading coefficient, they will cancel each other. Then the degree on the L.H.S. is $3(n-1)$ . On the R.H.S., $f(x)^2$ is a polynomial of degree $2n$ . Equating degrees we have $3(n-1)=2n \Rightarrow n=3$ . Our polynomial is then $ax^3+bx^2+cx+d$ . Now comes the expansion.

Plugging in $x^3$ is no problem, yielding $ax^9+bx^6+cx^3+d$ . Plugging in $x^3-2$ gives $[a(x^9-6x^2+12x^3-8)+b(x^6-4x^3+4)$ $+c(x^3-2)+d]$ . Distributing and collecting like terms gives $[6a]x^6+[c-12a]+4b]x^3+[8a-4b+2c]$ . On the R.H.S., we must compute $(ax^3+bx^2+cx+d)^2+12= [a^2]x^6+[2ab]x^5$ $+[b^2+2ac]x^4+[2ad+2bc]x^3+[c^2+2bd]x^2+[2cd]x$ $+[d^2+12]$ . Matching coefficients for $x^6$ we find that $a^2-6a=0 \Rightarrow \boxed{a=6}$ , nonzero as we must have degree 3. Then we have for $x^5, 2ab=0\Rightarrow \boxed{b=0}$ . For $x^4, b^2+2ac=0=12c \Rightarrow \boxed{c=0}$ , and for the constant term we have $8a-4b+2c=d^2+12 \Rightarrow \boxed{d=\pm 6}$ .

Now $f(x)=6x^3 \pm 6$ , so either $-1$ or $1$ is a root. Testing the positive value, we have that $-1$ is a root of $f(x)=6x^3+6$ . Then by the given equation, $f(-1)+f(-3)=f(-1)^2+12 \Rightarrow f(-3)=12$ , but for $x<-1, f(x)<0$ because a is positive, a contradiction. Thus we choose the negative value and finally $f(x)=6x^3-6$ , and $f(5)=6\cdot 125 - 6 = 744$

Since the question disallows constant polynomials as solutions I defined f in the following code as a quadratic first, then as a cubic. The quadratic failed to yield a feasible solution.

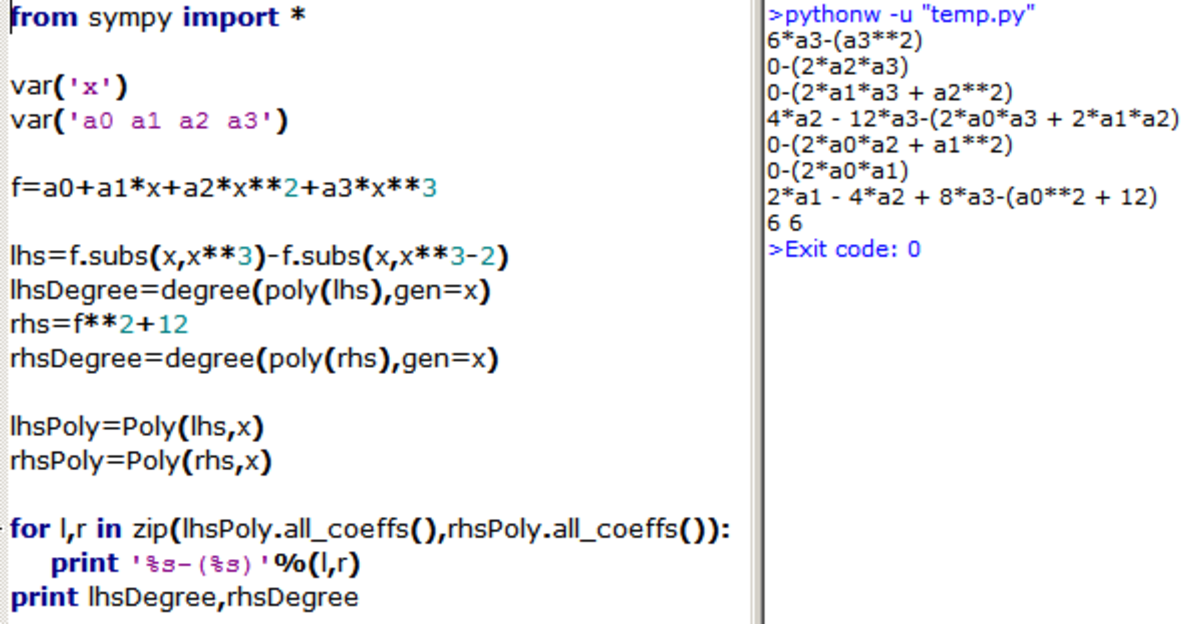
As in one or two other solutions here, the program simply uses the Python sympy symbolic algebra code to work out the coefficients of the polynomials on either side of the given functional equation. I solved for their values in a separate window, then evaluated the function at the required value of the indeterminate.

Let f(x) = $ax^3+bx^2+cx+d$

Substituting in the equation, we get: LHS:

• $(ax^9+bx^6+cx^3+d)-[a(x^3-2)^3+b(x^3-2)^2+c(x^3-2)+d]$
• $(ax^9+bx^6+cx^3+d)-[a(x^9-6x^6+12x^3-8)+b(x^6-4x^3+4)+c(x^3-2)+d]$
• $6ax^6+(4b-12a)x^3+8a-4b+2c$

RHS:

• $=(ax^3+bx^2+cx+d)^2+12$
• $=a^2x^6 +b^2x^4+c^2x^2+d^2+2abx^5+2bcx^3+2cdx+2acx^4 +2adx^3 +bdx^2+12$
• $=a^2x^6 +2abx^5 +(b^2+2ac)x^4+(2bc+2ad)x^3+(c^2+bd)x^2+2cdx+(d^2+12)$

From here, we get the following equations:

1. $2abx^5=0x^5$
2. $(b^2+2ac)x^4=0x^4$
3. $(c^2+bd)x^2=0x^2$
4. $2cdx=0x$
5. $a^2x^6=6ax^6$
6. $(2bc+2ad)x^3=(4b-12a)x^3$
7. $(d^2+12)=8a-4b+2c$

Using the first two equations: > $b^3+2abc = 0$ > $\rightarrow b^3 + 0c = 0$ > $\rightarrow b=0$

Using equations 3 and 4: > $c^3+bcd=0$ > $\rightarrow c^3 + b(0)=0$ > $\rightarrow c=0$

Using equations 5, 6, and the fact that b and c are 0: > $a^2 = 6a \rightarrow a(a-6)=0 \rightarrow a=0$ or $a=6$

> But $(d^2+12)=8a-4b+2c \rightarrow d^2 = -12 +8a \rightarrow a \neq 0$ >Therefore, $a=6$

Using equation 6 and the fact that a=6: > $2bc+2ad=4b-12a \rightarrow 2ad = -12a \rightarrow d=-6$

Check if the solutions are consistent using equation 7: > $(d^2+12)=8a-4b+2c \rightarrow 36 +12 = 48 - 0 + 0 \rightarrow 48=48$

Thus, $f(x) = 6x^3 - 6 \rightarrow f(5)=6(5^3)-6=744$

• Note: If we try to find a linear or quadratic function for f(x), we will get inconsistent solutions for a, b, c and d.

Given f(x) is a non-constant polynomial. Considering f(x) to be the most basic polynomials: f(x) = ax + b & f(x) = ax^2 +bx + c we see that the degrees in both sides of the equation do not match. But considering f(x) = ax^3 +bx^2 + cx +d we find that both sides of the equation have the same degree. So f(x) is a cubic equation. Putting f(x) = ax^3 +bx^2 + cx +d in the given equation and comparing the coefficients of powers of x we see that a = 6, b=c=0, d=-6 So f(x) = 6x^3 - 6 So f(5) = 6(125-1) = 744

Let $n=\deg f$ and $f(x)=ax^n+bx^{n-1}+\ldots$ , with $a\neq0$ . If we put this $f$ in the left hand side we get $f(x^3)-f(x^3-2)=\\=ax^{3n}+bx^{3n-3}+\ldots-a(x^3-2)^{n}-b(x^3-2)^{n-1}-\ldots=\\=ax^{3n}+bx^{3n-3}+\ldots-ax^{3n}-2nax^{3n-3}-\ldots-bx^{3n-3}-\ldots=\\=-2anx^{3n-3}+\ldots$ so, since $a\neq0$ , we have $deg(\text{LHS})=3n-3$ ; but this must also be equal to $\deg(\text{RHS})=2n$ , so we have $n=3$ and thus $f(x)=ax^3+bx^2+cx+d$ Putting this in the text and making the calculations we obtain [6ax^6+(4b-12a)x^3+(8a-4b+2c)=a^2x^6+2abx^5+x^4