Tripod
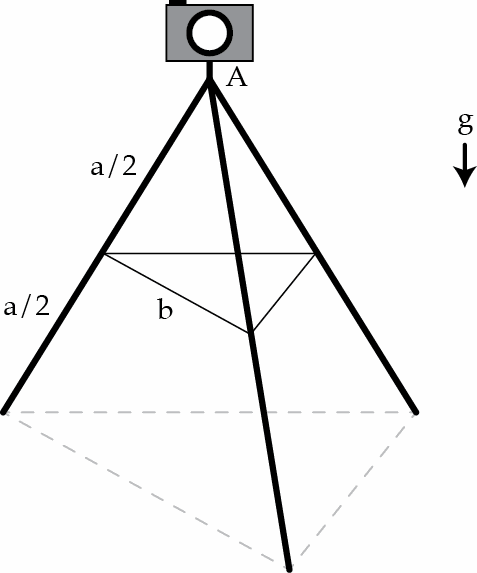
Consider a tripod consisting of three uniform bars (legs) of length a and mass m = 0 . 8 kg , freely jointed at point A. The middle points of the legs of the tripod are joined by 3 massless strings of length b . The tripod rests on a smooth surface while supporting a camera of mass M = 1 kg . If b a = 4 determine the tensions T in Newtons in the strings. Assume g = 9 . 8 m / s 2 .
The answer is 2.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
What is this:
24 people did the question before an hour (2 days, 11 hours) and 9 people did in an hour after the first solution got posted.
Log in to reply
That's always the case. I have seen that once a solution is posted, the number of people who have solved the problem increases in number.
For instance, I suggest you to follow the problem "Polynomials with no Common Factors" in the Algebra section. Only a few have solved it and no solutions has been posted (And I eagerly wait for the solution :P ).
smooth
Hi Jatin, nice solution! I have one stupid question: must we take A as the pivot? What about the mid-point of the rod or the bottom where the leg touches the ground? This baffled me and Thats why couldn't come up with the correct answer. Thank you.
Log in to reply
Check my solution. :)
In rotational dynamics we can consider forces acting at any point on the radius around the axis as part of the same system and still take into account the forces whether they're mid-way into the rod or at the bottom. This idea is what makes jatin's method so simple. Innovative thinking by jatin..
Why is PB b/sqrt(3) and tan(theta)=1/sqrt(11)?
Log in to reply
The distance from a vertex of an equilateral triangle to the center is sidelength divided by 3 which you could show using the law of cosines. This is the horizontal distance P B ˉ . Given that, cos θ can be found using cos = 1 − sin 2 → cos = 1 − 1 2 1 = 2 3 1 1 . Given that, tan θ is obviously 1 1 1 .
Lets set up a coordinate system with origin at one of the legs of tripod.
 Tripod
Tripod
G is the centroid of triangle OBC.
The coordinates can be easily found out, I am skipping that task.
Note the CM of the complete system lies on the blue line, I haven't shown the exact position of it as it is not required.
There are some unknown forces at the pivot but since they cancel, we don't have to care about including them in the force balance equation.
I have only shown the tension force acting on the leg OA.
Since the system is at rest or equilibrium, the net force is zero. Summing the forces in the y-direction,
N 1 + N 2 + N 3 = ( M + 3 m ) g = 3 . 4 g
From the symmetry, we can conclude that N 1 = N 2 = N 3 = N
Hence, N = 3 . 4 g / 3 .
Next we balance the moments of forces on leg OA about point A. The point A is chosen because the moment of the unknown forces mentioned before is zero.
The force acting at point D is: F D = T i ^ + 2 T i ^ + 2 T 3 k ^ − m g j ^
⇒ F D = 2 3 T i ^ − m g j ^ + + 2 T 3 k ^
The force acting on leg OA at origin is: F O = N j ^ .
The net moment of the forces about A is: A D × F D + A O × F O = 0
We have
A D = O D − O A = 2 − b i ^ + ( − b ) 3 1 1 j ^ + 2 3 − b k ^
and
A O = − b i ^ + ( − 2 b ) 3 1 1 j ^ + 3 − b k ^
Evaluating the cross products is trivial. Equate any of the component of the net moment to zero to get the value of T.
For instance, equating the x component to zero, you end up with
3 N = 2 T 1 1 + 2 3 m g
Solving for T, T = 2 . 5 0 2 0 8 N .
I do understand that its a quite long solution. I am interested to know how other members approached this.
I took the utmost care to prevent my solution from errors. I am sorry if errors have prevailed.
Log in to reply
Nicely done Jatin! I came up with that solution at midnight and I really couldn't think of a smarter way, your method is elegant. Thank you for sharing the solution. :)
this solution is a triumph of the human spirit
Log in to reply
Ah, come on ! That's rude ! This is an equally good solution with just an 'elaborate' explanation..
Log in to reply
i don't mean anything negative in my comment. i don't think i could have followed through with this line of solution if it happened to be the one that i picked. i'm actually impressed that a human could do this perfectly within 3 tries.
Log in to reply
@Josh Silverman – I myself don't know what gave me the courage to go along this method, I was too afraid of getting the wrong answer as I am very inexperienced with 3-D Geometry and Vectors. I got the answer wrong in the first try. I checked my work more than 5 times and in the second try, I got the right answer. :)
But really, I admire Jatin's way of approaching the problem. Its a lot easier than my cumbersome approach.
Wow! Brilliant solution Pranav!! Using your picture as the illustration, I answered this problem by only considering torques in Δ AGO . Anyway, I rarely vote up solution here but your solution deserves my + 1 .
Log in to reply
I am very glad to know that, thank you Tunk! :)
Consider the forces that act upon one rod. These are the weight of the camera M g , the weight of the rod itself m g , the normal force on the point that touches the ground M / 3 + m g (this is true since the projections of forces on the vertical axis are equal as the system is in equilibrium) and the resultant force F from tensions T of two strings.
Since the system is in equilibrium, the sum of moments of forces must equal zero. Let an angle that the rod makes with the ground be α and let the angle 2 π − α = β . Then the moments of forces about point A are the following: $$M_{Mg} = 0\text{,}$$
\begin{array} \\ M {mg} &= \int 0^a a' g \sin{\beta} dm \\ &= \int_0^a a' g \sin{\beta} \rho da' \\ &= \frac{mg a \sin{\beta}}{2}, \\ \end{array}
$$M_F = \frac{Fa\sin{\alpha}}{2},$$
$$M_N = Na \sin{\beta} = (\frac{M}{3} + m)ga \sin{\beta}.$$
Equating the sum of moments with 0 , making some algebraic manipulations and noting that sin β = cos α we get that $$F = g (\frac{2M}{3} + m) \cot{\alpha} \text{ } (*).$$
Now express F in terms of T . It can be done using the Law of Cosines and considering a rhombus with side length T , angle of 6 0 ∘ and greater diagonal F . It follows that F = T 2 ( 1 + cos 6 0 ∘ ) = T 3 ) .
Substituting this expression for F into ( ∗ ) we get $$F = \frac{1}{\sqrt{3}} g (\frac{2M}{3} + m) \cot{\alpha}$$
Now all that's left is to find α . First, consider the side of our pyramid. Once again, use Law of Cosines to get that the plane top angle is cos − 1 8 7 and that the side base is of length 2 a . Then, consider the base and use Law of Cosines to find that the distance from the height of the pyramid to one of the base vertices is 1 2 a . Use Pythagoras theorem to find that the height of the pyramid is 2 a 3 1 1 . Hence, cot α = 1 1 1 .
Plugging the numbers in we get $$T = \frac{1}{\sqrt{11 * 3}} \cdot 9.8 \cdot (0.8 + \frac{2}{3}) = \boxed{2.5 \text{ (N)}}$$.
Consider the forces on system , there are 3 upward normal reactions ( N ) each from the ground on legs of tripod , and the weight of system , Balancing force on the system, we get :
N = 3 3 m g + M g .
Now , consider B , C and D be the vertices of triangle made by massless strings and P as the centroid of triangle. Let θ be the angle made by a rod with vertical,
In △ A P B , s i n θ = A B P B = 2 a 3 b = 2 3 1 , ⇒ t a n θ = 1 1 1 .
Now , firstly net force of tension acting on B = 2 T c o s 6 π = T 3
Balance torque on a rod about A to get,
N a s i n θ = m g 2 a s i n θ + T 3 2 a c o s θ
⇒ T = 3 2 N − m g t a n θ = 3 3 3 2 M g + 3 m g = 2 . 5