Try geometry
f ( x ) = x 2 + 1 2 1 + x 2 − 1 4 x + 2 1 8
Determine the value of x that minimizes the function above.
If x = b a , where a and b are positive coprime integers, then find a + b .
The answer is 101.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
First, rewrite f ( x ) as f ( x ) = x 2 + 1 1 2 + ( x − 7 ) 2 + 1 3 2 .
Now draw a line B C of length 7 . Next, draw a line A B of length 1 1 extending upward from B perpendicular to B C , and a line C D of length 1 3 downward from C perpendicular to B C . Let P be a point on B C such that ∣ B P ∣ = x , making ∣ P C ∣ = 7 − x .
Then since we will then have ∣ A P ∣ 2 = ∣ A B ∣ 2 + ∣ B P ∣ 2 = 1 1 2 + x 2 and ∣ P D ∣ 2 = ∣ P C ∣ 2 + ∣ C D ∣ 2 = ( 7 − x ) 2 + 1 3 2 , we see that f ( x ) = ∣ A P ∣ + ∣ P D ∣ .
Now by Fermat's principle we know that f ( x ) will be minimized when A D is a straight line, in which case Δ A B P and Δ D C P are similar. This in turn implies that
∣ B P ∣ ∣ A B ∣ = ∣ P C ∣ ∣ C D ∣ ⟹ x 1 1 = 7 − x 1 3 ⟹ 7 7 − 1 1 x = 1 3 x ⟹ x = 2 4 7 7 .
Thus a + b = 7 7 + 2 4 = 1 0 1 .
Why are all the 'famous' problems in community section, your problems? Give someone else a chance. It is so unfair.
Log in to reply
I'm sorry about this. It was never my intention to monopolize the Popular section; I was just resharing some of my problems from years ago so that newer members could try them out. I thought they would just show up in the New section but they ended up all showing in the Popular section as well. Perhaps this is a glitch in the algorithm this site uses that could be fixed, so that only more recent problems are eligible for the Popular section. Would you like me to ask staff to look into this? I don't know how to de-popularize my problems, other than deleting them forever which I am hesitant to do. Others have commented positively about them and many new solutions have been posted as well, but I do agree that this doesn't seem quite fair; they should probably only be allowed to show up in the New section, or do you object to that too?
I understand your frustration. But problems and solution by Brian Charlesworth are one of the most important part of Brilliant. He is one who never tries to push himself up, though he is so popular and has deep knowledge of math. I agree with you that
problems by other also should appear in Popular section.
I don't object to the problems showing in the popular or new section. I'm just saying there shouldn't be so many of those made by one person. I've been making new problems lately and none of them end up in the popular section like they used to. And so they end up getting ignored.
Log in to reply
I can understand your frustration. The Popular section should be refreshed more often so that the same problems, (particularly at the moment with all of them being by the same author), don't stay at the top of the list for so long. I've asked a staff member (Andrew Hayes) about the issue so I hope to hear back from him in the next few days. I realize now what I should have done in resharing old problems was to post new versions of them instead so that they wouldn't automatically end up in the Popular section. I'm sorry again that they all ended up there, but I don't want to delete them so I'll have to wait for Andrew to respond.
P.S.. I just noticed that one of your problems is now at the top of the Popular section. That's a start, anyway. :)
Andrew Hayes got back to me and said that staff will try to popularize other problems so that mine won't dominate the spotlight anymore. They won't be changing the algorithm that chooses which questions end up in the Popular section, however, so I'll stop resharing old problems in order to avoid monopolizing the section again.
Log in to reply
I think you should NOT stop re-sharing. Let a staff member decide what to do. Your problems and solutions are very useful to many many members. Popularize other problems is the solution, without disturbing what you are doing.
Log in to reply
@Niranjan Khanderia – Thank you for the encouragement, Niranjan. I think I will however wait until enough other questions are popularized before resharing more old problems of mine. When a contributor's questions are popularized it encourages them to post more new problems, and the more contributors who experience this the better. The rate of creation of new problems has been declining for some time and needs all the help it can get. Staff has mentioned that they have no plans to change the algorithm that decides which problems are elevated to the Popular section, so for that reason as well I will stop resharing for the next while.
Log in to reply
@Brian Charlesworth – Thanks for your reply. I am not at a level to encourage you. I was just telling Rane how modest you are. With best wishes, Niranjan.
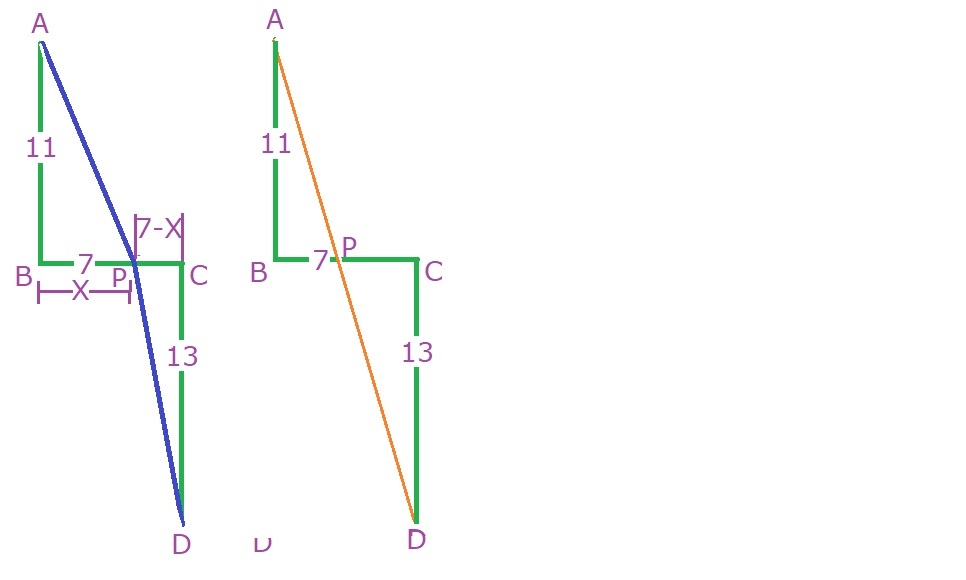
sketch of solution by Brian Charlesworth .
Log in to reply
Thank you for creating the image; it's very helpful. :)
very interesting approach
Calculus approach
f ( x ) = x 2 + 1 2 1 + x 2 − 1 4 x + 2 1 8 ⟹ f ′ ( x ) = x 2 + 1 2 1 x + x 2 − 1 4 x + 2 1 8 x − 7
f ( x 0 ) ≤ f ( x ) , ∀ x ∈ R ⟹ f ′ ( x 0 ) = 0
x 0 2 + 1 2 1 x 0 + x 0 2 − 1 4 x 0 + 2 1 8 x 0 − 7 = 0 ⟹ x 0 2 + 1 2 1 x 0 2 − 1 4 x 0 + 2 1 8 = x 0 − ( x 0 − 7 )
x 0 2 + 1 2 1 x 0 2 − 1 4 x 0 + 2 1 8 = ( x 0 x 0 − 7 ) 2 ⟺ x 0 2 + 1 1 2 ( x 0 − 7 ) 2 + 1 3 2 = x 0 2 ( x 0 − 7 ) 2 ⟺
⟺ ( x 0 − 7 ) 2 ( x 0 − 7 ) 2 + 1 3 2 = x 0 2 x 0 2 + 1 1 2 ⟹ 1 + ( x 0 − 7 ) 2 1 3 2 = 1 + x 0 2 1 1 2
[ ( x 0 − 7 ) 1 3 ] 2 = ( x 0 1 1 ) 2 ⟹ ∣ ∣ ∣ ∣ ( x 0 − 7 ) 1 3 ∣ ∣ ∣ ∣ = ∣ ∣ ∣ ∣ x 0 1 1 ∣ ∣ ∣ ∣ ⟹ ∣ 1 3 x ∣ = ∣ 1 1 ( x 0 − 7 ) ∣
x 0 ′ = 2 4 7 7 ∧ x 0 ′ ′ = − 2 7 7 ⟹ f ( x 0 ′ ) = 2 5 ∧ f ( x 0 ′ ′ ) ≈ 8 7 . 3 6
⟹ f ( x 0 ′ ) < f ( x 0 ′ ′ ) ⟹ x 0 = x 0 ′ = 2 4 7 7 ⟹ a + b = 7 7 + 2 4 = 1 0 1
Thanks for providing this solution. It's more efficient than the calculus approach I scribbled out on paper. :)
Note that f ′ ( − 2 7 7 ) is the sum of two negative terms, so x 0 ′ ′ is an extraneous solution that doesn't actually solve f ′ ( x ) = 0 .
The only possibility for solutions is if the two terms of the derivative have opposite signs, so x must be between 0 and 7, like x 0 ′ = 2 4 7 7 .
Nice one! This inequality is called the Cauchy-Schwarz inequality (https://brilliant.org/wiki/cauchy-schwarz-inequality/).

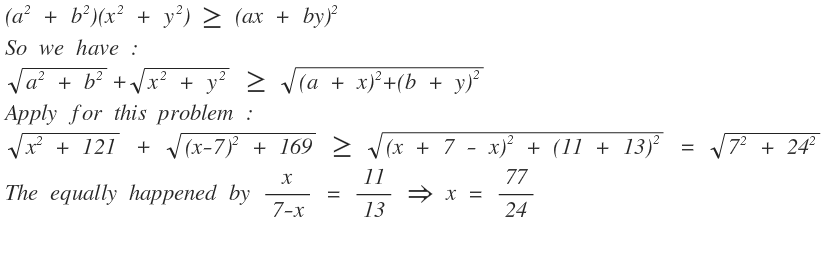
In the coordinate plane, let A = ( 0 , − 1 1 ) , B = ( 7 , 1 3 ) , and P = ( x , 0 ) . Then f ( x ) = A P + P B . The minimum occurs where A B crosses the x -axis. The equation of line A B is y = 7 2 4 x − 1 1 . Setting this to 0 and solving, we get x = 2 4 7 7 .