Try not to use L'Hôpital!

Calculus Level 2

Find the value of $\displaystyle\lim_{x\to0^+}x^x$ .

does not exist 0 1

-\infty

3 solutions

Chew-Seong Cheong
Jul 17, 2015

$\lim_{x \to 0^+} x^x = \lim_{x \to 0^+} x^{x+1-1} = \lim_{x \to 0^+} \dfrac{x^{x+1}}{x^1} = \dfrac{x}{x} = \boxed{1}$

Moderator note:

Great simple approach. Sometimes, if a problem is complicated by 2 parts, we can try to separate out these issues and due with them individually. (Of course, this might not always work.)

Nice solution!!!!! I could never come up with such a simple and beautiful solution.

Kenny Lau - 5 years, 11 months ago

You will. Just need more practice and learning. You are still very young.

Chew-Seong Cheong - 5 years, 11 months ago

I overlooked it. This solution is invalid. You can't just substitute $x=0$ to the index of the numerator but not to the base of the numerator. Either you write it as $x^{x+1}$ or $0^{0+1}$ .

Kenny Lau - 5 years, 11 months ago

@Kenny Lau – It is not $0$ but $0^+$ ; it has a small positive value. It is of course undefined when $x=0$ that is why the problem asks for $x \to 0^+$ . $x \to 0$ is not the same as $x = 0$ . $|x \to 0|$ has an infinitesimal value and $\ne 0$ . Therefore $\dfrac{x}{x} = 1$ is always true so long as $x$ has a value however small except $=0$ . For $x<< 1$ , we can assume $x+1=1$ . That is $\lim_{x \to 0} \dfrac{x}{x} = 1$ and $\lim_{x \to 0} x + 1 = 1$ . This is the same as $\lim_{x \to 0} \sin{x} = x$ but $\sin{0} = 0$ . This is because $\sin{x} = x - \frac{1}{6}x^3 + \frac{1}{240}x^5 - ...$ For very small $x$ , we can take $x^3 = x^5 =... = 0$ and $\sin{x} = x$ .

Chew-Seong Cheong - 5 years, 11 months ago

@Chew-Seong Cheong – But... how do you know $x^{x+1}\to x^1$ ?

Kenny Lau - 5 years, 11 months ago

@Kenny Lau – Like I have mentioned $x$ is very, very, very... (infinitesimally) smaller than $1$ so we can treat it as $0$ when compared with $1$ therefore, $\lim_{x\to 0} (x+1) = 0 + 1$ . We cannot say the same for $\frac{x}{x}$ because $x$ compared with $x$ is always $1$ .

Chew-Seong Cheong - 5 years, 11 months ago

@Chew-Seong Cheong – Oh... I apologize.

Kenny Lau - 5 years, 11 months ago

Israel Funa
Jul 17, 2015

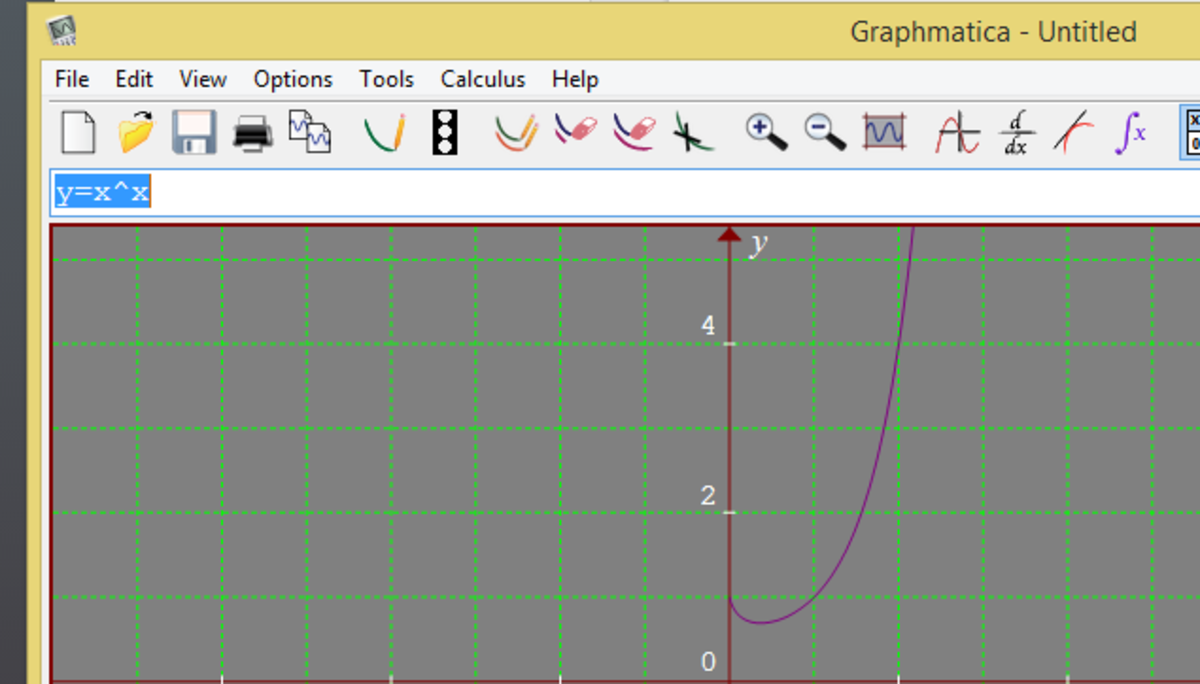
as x approaches to zero, y gets closer to 1

Nice solution! Personally, I use desmos frequently.

Kenny Lau - 5 years, 11 months ago

Kenny Lau
Jul 17, 2015

@Chew-Seong Cheong was the first one to post a solution that does not use L'Hôpital.

Maybe Squeeze Theorem would work, but I still cannot find a suitable lower bound. Below is the solution using L'Hôpital.

By the definition of real power: $x^x=\exp(x\ln x)$ where $\exp$ is the exponential function, equivalent to $e^x$ .

When $x\to0^+$ , $\ln x\to-\infty$ . Therefore, this is an indeterminate form of $0\times\infty$ .

It can be made to an indeterminate form of $\frac\infty\infty$ like this: $\displaystyle\lim_{x\to0^+}\exp(x\ln x)=\lim_{x\to0^+}\exp\left(\frac{\ln x}{1/x}\right)$ .

Applying differentiation to the denominator and the numerator: $\displaystyle\lim_{x\to0^+}\exp\left(\frac{\ln x}{1/x}\right)=\lim_{x\to0^+}\exp\left(\frac{1/x}{-1/x^2}\right)$ .

Simplify it to get $\lim_{x\to0^+}\exp\left(\frac{1/x}{-1/x^2}\right)=\lim_{x\to0^+}\exp(-x)$ .

Substitute $x=0$ in to get $\mbox1$ .