Try to solve it in a different way
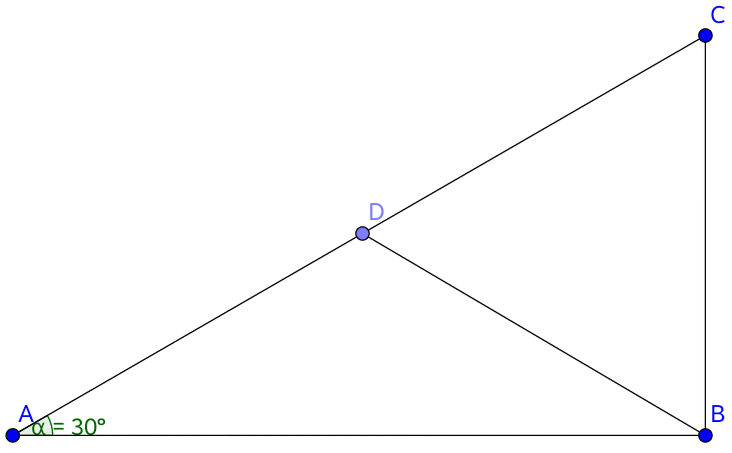
In the above figure, △ A B C is a right-angled triangle in which A C is the hypotenuse. ∠ B A C = 3 0 ∘ . D is the midpoint of A C . Then find the value of ∠ B D C .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Nice thought..+1..
Use sine rule in both small triangles as follows:- Given A D = D C = x (say) Now, sin ( A B D ) x = s i n 3 0 º B D ⟹ B D = s i n ( A B D ) ( x × s i n 3 0 º ) . ⟶ ( 1 ) Also, in the other triangle:- sin ( 9 0 − A B D ) x = s i n 6 0 º B D ⟹ B D = c o s ( A B D ) ( x . s i n 6 0 º ) ⟶ ( 2 ) Equating (1) & (2).. you get:- tan ( A B D ) = 3 1 ⟹ ∠ A B D = 3 0 º Now ∠ B D C = ∠ A B D + 3 0 º (exterior angle property) = 6 0 º . Thank you.
Yep will look nice with proper L A T E X
Log in to reply
I dont know it I m a beginner. .so can u help me please.?
Log in to reply
Yeah sure.
Use sine rule in both small triangles as follows:-
Given
A
D
=
D
C
=
x
(say)
Now,
sin
(
A
B
D
)
x
=
s
i
n
3
0
º
B
D
⟹
B
D
=
s
i
n
(
A
B
D
)
(
x
×
s
i
n
3
0
º
)
.
⟶
(
1
)
Also, in the other triangle:-
sin
(
9
0
−
A
B
D
)
x
=
s
i
n
6
0
º
B
D
⟹
B
D
=
c
o
s
(
A
B
D
)
(
x
.
s
i
n
6
0
º
)
⟶
(
2
)
Equating (1) & (2).. you get:-
tan
(
A
B
D
)
=
3
1
⟹
∠
A
B
D
=
3
0
º
Now
∠
B
D
C
=
∠
A
B
D
+
3
0
º
(exterior angle property) =
6
0
º
.
Thank you.
Log in to reply
@Ashish Menon – Wow.!!! The solution is now just amazing.+1. & thanx brother. But I use brilliant At phone, and the hamburger option u r talking about doesn't seem to be here. It is available when I read notes. There I can see 'toggle latex'. But not here. I m sorry if im disturbing you but can you suggest a site. Or wiki where I can learn to write in latex.? I think first of all I have to go through a computer basics course.
Log in to reply
@Rishabh Tiwari – You can refer here :) You are never disturbing :)
Log in to reply
@Ashish Menon – Help me with this REALLY REALLY HARD GEOMETRY QUESTION
Log in to reply
@Jason Chrysoprase – Yeah I am trying ita tough ;)
@Ashish Menon – Thank you Ashish. I will learn it at my laptop.
Log in to reply
@Rishabh Tiwari – @Rishabh Tiwari Can you guys help me solve this REALLY REALLY HARD GEOMETRY QUESTION
Log in to reply
@Jason Chrysoprase – Sure sir . Im trying it. Hard problem..
Log in to reply
@Rishabh Tiwari – Update it in your solution. And for beginning in a new line, you have to leave 3 spaces after each line. Plz add them wherever the \ sign is not present. For example, if there is a line "Hahaha" which is written outside LaTeX brackets, then you have to leave 3 spaces and then press enter and begin on a new line, But if you are using LaTeX brackets then \ signifies ine line break. I have put those \ in my solution, but plz add those 3 spaces wherever LaTex brackets are not present if you want to make a new line because Toggle LaTex does not show that.
Now, go to the top right corner of your screen. There you can see a hamburger option which you can use for editing this question. In the dropbox which would appear soon click "Toggle LaTeX". Then scroll this comment of mine and you would see the LaTeX codes i used. Copy the whole thing and put it in your solution. THEN, erase the words
Latex:
You would see the word
Latex
and a semicolon
:
in my solution after putting it in your solution delete them. Then publish it! And let me know :).
In △ A B C , A C is the hypotenuse, so ∠ A B C = 9 0 ∘ .
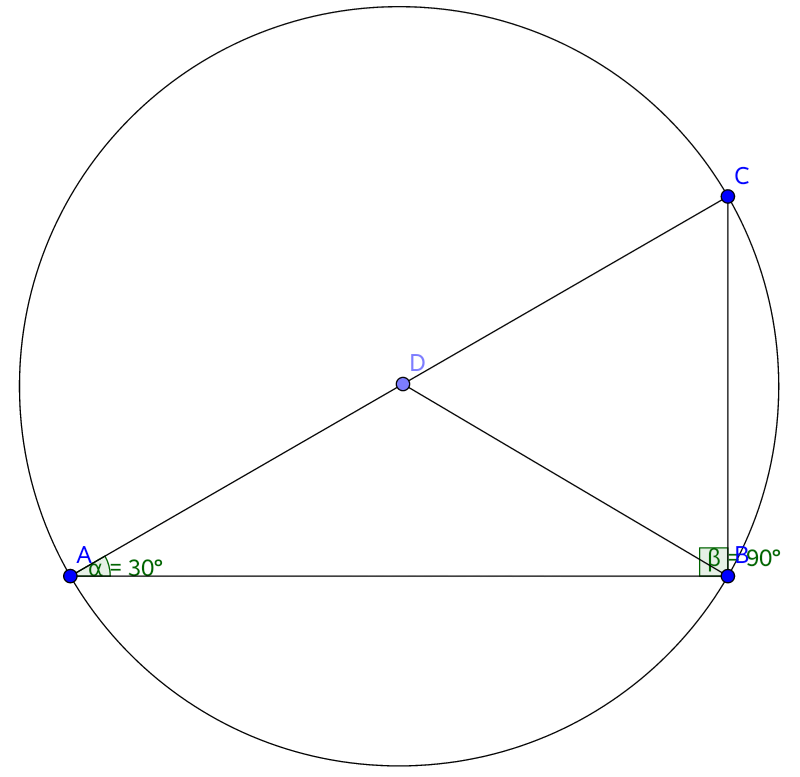
The minimum number of points required for a circle to pass through = 3 points.
Draw the circumcircle of △ A B C .
Now, ∠ A B C = 9 0 ∘ .
The angle inside a semicircle is a right angle.
So, A C is the diameter of the circle.
∴ D is the center of the circle. (Mid-point of the diameter of the circle is the center of the circle)
∴ ∠ B D C = 2 ∠ B A C (Angle at the centre is twice the angle at the remaining part of the circle).
⟹ ∠ B D C = 2 × 3 0 ∘ = 6 0 ∘ .
Q.E.D