Twice as Big
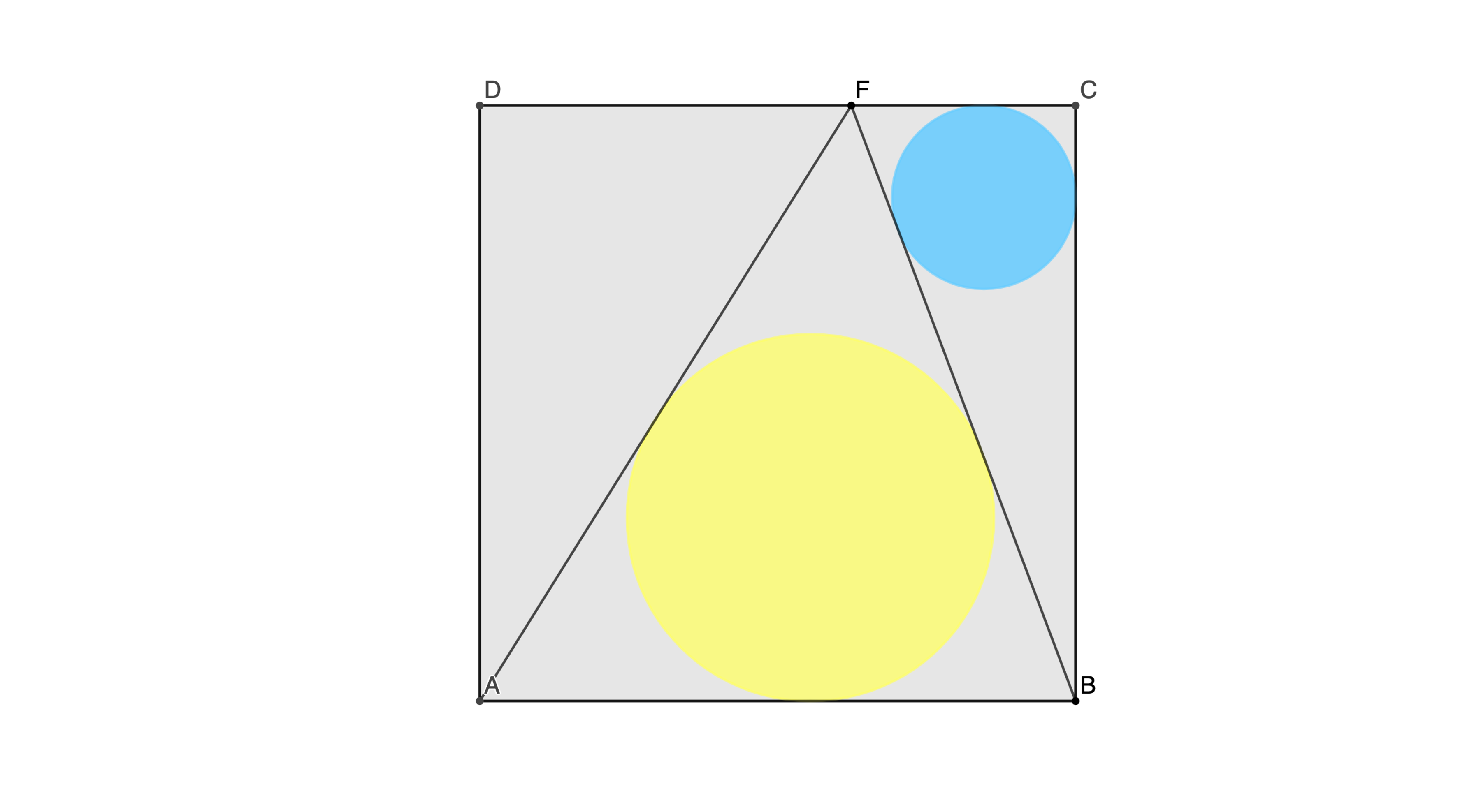
F is chosen on the unit square A B C D so that the radius of the yellow circle is twice the radius of the blue circle. If the yellow radius is a root of f ( x ) = a x 3 + b x 2 + c x + d , where g cd ( a , b , c , d ) = 1 , and a > 0 , find f ( 6 ) .
The answer is 29.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
"After some algebra" is a bit understated. :). Good job! The cubic for r is correct, but I don't understand how you got from there to f ( x ) = 2 x 3 − 1 2 x 2 + 5 x − 1 .
Log in to reply
If r is the root to the polynomial g ( X ) = 8 X 3 − 2 4 X 2 + 1 2 X − 1 , then 2 r is the root to the polynomial g ( 2 X ) = 2 X 3 − 1 2 X 2 + 5 X − 1 .
Log in to reply
Got it. Thank you.
Log in to reply
@Fletcher Mattox
–
@Fletcher Mattox
@Pi Han Goh
- Sorry, there are two copy-paste typos in my solution.
1) I put the wrong equation as the result of this dizzying "some algebra" I tackled.
2) The coefficients in
f
(
x
)
are also not the ones I had finally got (obviously, the correct answer didn’t come from the polynomial I wrote).
I have edited these typos. I thought that writing "after some algebra" would be enough to skip this boring manipulation, but, for Fletcher :), I've added the missing steps.
Log in to reply
@Thanos Petropoulos – Ahh, and I thought something went wrong with my calculation.
Fantastic attached image and solution as always. Thank you.
@Thanos Petropoulos – @Thanos Petropoulos your solutions are always a joy to read. Thank you!
Log in to reply
@Fletcher Mattox – @Fletcher Mattox , @Pi Han Goh - Thank you both. Again I'm sorry for the confusion my original text has caused.
Since 2 r < 1 , we get 8 r 3 − 2 4 r 2 + 1 0 r − 1 = 0 ⇔ ( 2 r ) 3 − 6 ( 2 r ) 2 + 5 ( 2 r ) − 1 = 0 From this we see that the radius 2 r of the yellow circle is a root of f ( x ) = x 3 − 6 x 2 + 5 x − 1 .
For the answer, f ( 6 ) = 2 9 .