TwistedSquares 2
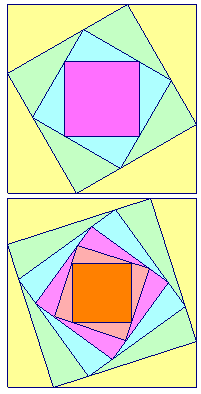
The upper picture shows 3 squares nested inside the outer square, each rotated 3 9 0 ∘ = 3 0 ∘ from the one outside it.
The lower picture shows 5 squares nested inside the outer square, each rotated 5 9 0 ∘ = 1 8 ∘ from the one outside it.
Let us consider making n squares nested inside the outer square, each rotated n 9 0 ∘ from the one outside it. If a is the side length of the smallest square divided by the side length of the largest square, find n → ∞ lim a .
The answer is 0.2078795764.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Okay, better go check WolframAlpha, because the limit is e − 2 π = 0 . 2 0 7 8 7 9 5 7 6 4
Incidentially, i i = e − 2 π
In the limiting case, we have the classic logarithmic spiral r = a ⋅ e b θ in polar coordinates, where a is arbitrary but b = 1 if it always makes an angle of 4 5 degrees with the radial line to the origin. So, for a quarter turn, the ratio is e − 2 π
Log in to reply
Thanks. I've updated the answer to 0.2078795764. Those who previously answered 0.2078795764 has been marked correct.
I've also updated the last line of Jeremy's solution.
At the beginning,I started from the inside.
If the smaller rectangle's side length is 1,then it's simple to see that the bigger one's side length is sin θ + cos θ
Sorry for the confusion. I was confusing myself over whether to make the problem be about side length or area and I made a mistake when I switched back and forth. Area would have made the answer e − π and when I switched back to side length I misplaced the division.
Relevant wiki: L'Hopital's Rule - Basic
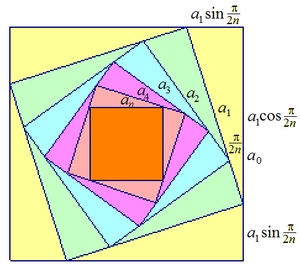 Let the side lengths of the largest square to the smallest square be
a
0
,
a
1
,
a
2
...
a
n
respectively. We note that
Let the side lengths of the largest square to the smallest square be
a
0
,
a
1
,
a
2
...
a
n
respectively. We note that
a 0 ⟹ a 1 a 2 a 3 ⋯ ⟹ a n a = a 1 sin 2 n π + a 1 cos 2 n π = sin 2 n π + cos 2 n π a 0 = sin 2 n π + cos 2 n π a 1 = ( sin 2 n π + cos 2 n π ) 2 a 0 = ( sin 2 n π + cos 2 n π ) 3 a 0 = ⋯ = ( sin 2 n π + cos 2 n π ) n a 0 = a 0 a n = ( sin 2 n π + cos 2 n π ) n 1 Similarly,
n → ∞ lim a = n → ∞ lim ( sin 2 n π + cos 2 n π ) n 1 = exp ( n → ∞ lim − n ( sin 2 n π + cos 2 n π − 1 ) ) = exp ( x → 0 lim − 2 π ( x sin x + cos x − 1 ) ) = exp ( − 2 π ( x → 0 lim x sin x + x → 0 lim x cos x − 1 ) ) = exp ( − 2 π ( 1 + x → 0 lim 1 − sin x ) ) = exp ( − 2 π ( 1 + 0 ) ) = e − 2 π ≈ 0 . 2 0 8 A 1 ∞ case, the following applies ⟹ x → ∞ lim ( f ( x ) ) g ( x ) = e lim x → ∞ g ( x ) ( f ( x ) − 1 ) Let x = 2 n π A 0/0 case, L’H o ˆ pital’s rule applies Differentiate up and down w.r.t. x
Reference: Limit for 1 ∞ case, see method 2 .
Could you elaborate on that second step on the limit? specifically what I do not get is: x → ∞ lim ( f ( x ) ) g ( x ) = exp ( ln ( x → ∞ lim ( f ( x ) ) g ( x ) ) ) = exp ( x → ∞ lim g ( x ) ln ( f ( x ) ) ) = ? exp ( x → ∞ lim g ( x ) ( f ( x ) − 1 ) )
Log in to reply
Check out the reference: Limit for 1 ∞ , see method 2 .
Log in to reply
Ok, I guess a general property here could be stated as: given lim x → a f ( x ) = 0 and lim x → a g ( x ) = ∞ then
x → a lim ( 1 + f ( x ) ) g ( x ) = exp ( x → a lim f ( x ) g ( x ) )
This makes intuitive sense to me (I haven't proven anything). Am I right?
Log in to reply
@Jose Fernandez Goycoolea – I am not sure whether you are right.
As the other solutions show, we have a = ( sin 2 n π + cos 2 n π ) − n , and we want to find L = n → ∞ lim a . In this present form, we cannot use L'Hopital's rule to find the limit, but the f ( n ) n form of a suggests that taking the natural logarithm of the limit might yield some results. So we proceed:
L ln L ln L = n → ∞ lim ( sin 2 n π + cos 2 n π ) − n = n → ∞ lim ln ( sin 2 n π + cos 2 n π ) − n = n → ∞ lim − n ln ( sin 2 n π + cos 2 n π ) .
From here, we can turn the limit into an 0 0 indeterminate form by writing − n as − n 1 1 , which we can apply L'Hopital's on:
ln L ln L = n → ∞ lim − n 1 ln ( sin 2 n π + cos 2 n π ) = n → ∞ lim n 2 1 sin 2 n π + cos 2 n π 1 ⋅ ( cos 2 n π − sin 2 n π ) ⋅ ( − 2 n 2 π ) .
(See the Addendum at the bottom for the calculation of the derivative of ln ( sin 2 n π + cos 2 n π ) . )
Cleaning up the expression, we finally have
ln L ln L ln L L = n → ∞ lim 2 π sin 2 n π + cos 2 n π sin 2 n π − cos 2 n π = 2 π ⋅ 0 + 1 0 − 1 = − 2 π = e − π / 2 ,
which is approximately 0 . 2 0 8 to three decimal places. ■
Addendum : To find the derivative of ln ( sin 2 n π + cos 2 n π ) , we have to apply the chain rule twice: once on the expression in the natural log, and once on the sine and cosine expressions.
d n d [ ln ( sin 2 n π + cos 2 n π ) ] = sin 2 n π + cos 2 n π 1 ⋅ d n d [ sin 2 n π + cos 2 n π ] = sin 2 n π + cos 2 n π 1 ⋅ ( cos 2 n π − sin 2 n π ) ⋅ d n d [ 2 n π ] = sin 2 n π + cos 2 n π 1 ⋅ ( cos 2 n π − sin 2 n π ) ⋅ ( − 2 n 2 π ) .
If x = 2 n π for large n , then the series expansion of S i n ( x ) + C o s ( x ) is
S i n ( x ) + C o s ( x ) = 1 + x − 2 1 x 2 − . . . , so that
x → 0 lim ( S i n ( x ) + C o s ( x ) ) − x 1 = x → 0 lim ( 1 + x ) − x 1 = e − 1
Letting x = 2 n π , we have
n → ∞ lim ( S i n ( 2 n π ) + C o s ( 2 n π ) ) − π 2 n = e − 1
or
n → ∞ lim ( S i n ( 2 n π ) + C o s ( 2 n π ) ) − n = e − 2 π
First, we need to find how the sides shrink based on the angle. tan θ = x 1 − x so x = tan θ + 1 1 . Also, cos θ = y x .
Put these together and you get y = c o s θ ( tan θ + 1 ) 1 = s i n θ + cos θ 1
So this is the ratio from one square to the next smaller. Working in radians θ = 2 n π and the ratio is applied n times so we seek
lim n → ∞ ( sin 2 n π + cos 2 n π ) − n
Which WolframAlpha tells me is e − π / 2 ≈ 0 . 2 0 7 8 7 9 5 7 6 4