Two Children Play With Three Coins
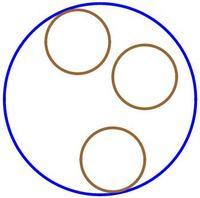
Two children collaborate on a problem for amusement. They place three coins, all of which are unit circles, inside a circular playing field of radius R .
They take turns making a move, with the following provisions
1) One coin is moved in each turn, not necessarily (but may be) in a straight path, sliding it from where it is to a new position inside the circular playing field without disturbing the other two coins,
2) such that the center of the moved coin slides past the line connecting the centers of the other two coins (i.e., sliding between the other two coins) exactly once ,
3) and to a new position not necessarily having to (but may) touch any of the other two coins or the border of the circular playing field.
4) The same coin may not be moved in two consecutive turns.
5) The two children deliberately play in such a way to make possible taking turns indefinitely, i.e., not being forced to stop playing because it has become impossible to move a coin and have its center pass through the line connecting centers of the other two coins without disturbing them.
6) The two children deliberately at the start place the three coins in the circular playing field in such a way that such indefinitely extended play is made possible.
What is the infimum radius R of the circular playing field for this to be possible?
Submit your answer as ⌊ 1 0 0 0 R ⌋ .
The answer is 4000.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
I can get a radius arbitrarily close to 4.
To be definite, I'm going to use coordinates. Let ϵ be any positive real number. Let the playing field be centered at ( 0 , 0 ) with radius 4 + 4 ϵ . Consider a red coin centered at ( 3 + 3 ϵ , 0 ) , a blue coin centered at ( − 3 − 3 ϵ , 0 ) , and a yellow coin centered at ( 1 + ϵ , ϵ ) .
First move: Move the red circle around the yellow coin.
Second move: Move the yellow coin to ( − 1 − ϵ , − ϵ ) .
Third move: Move the blue coin around the yellow coin.
Fourth move: Move the yellow coin back to ( 1 + ϵ , ϵ ) .
Then go back to the first move, and repeat.
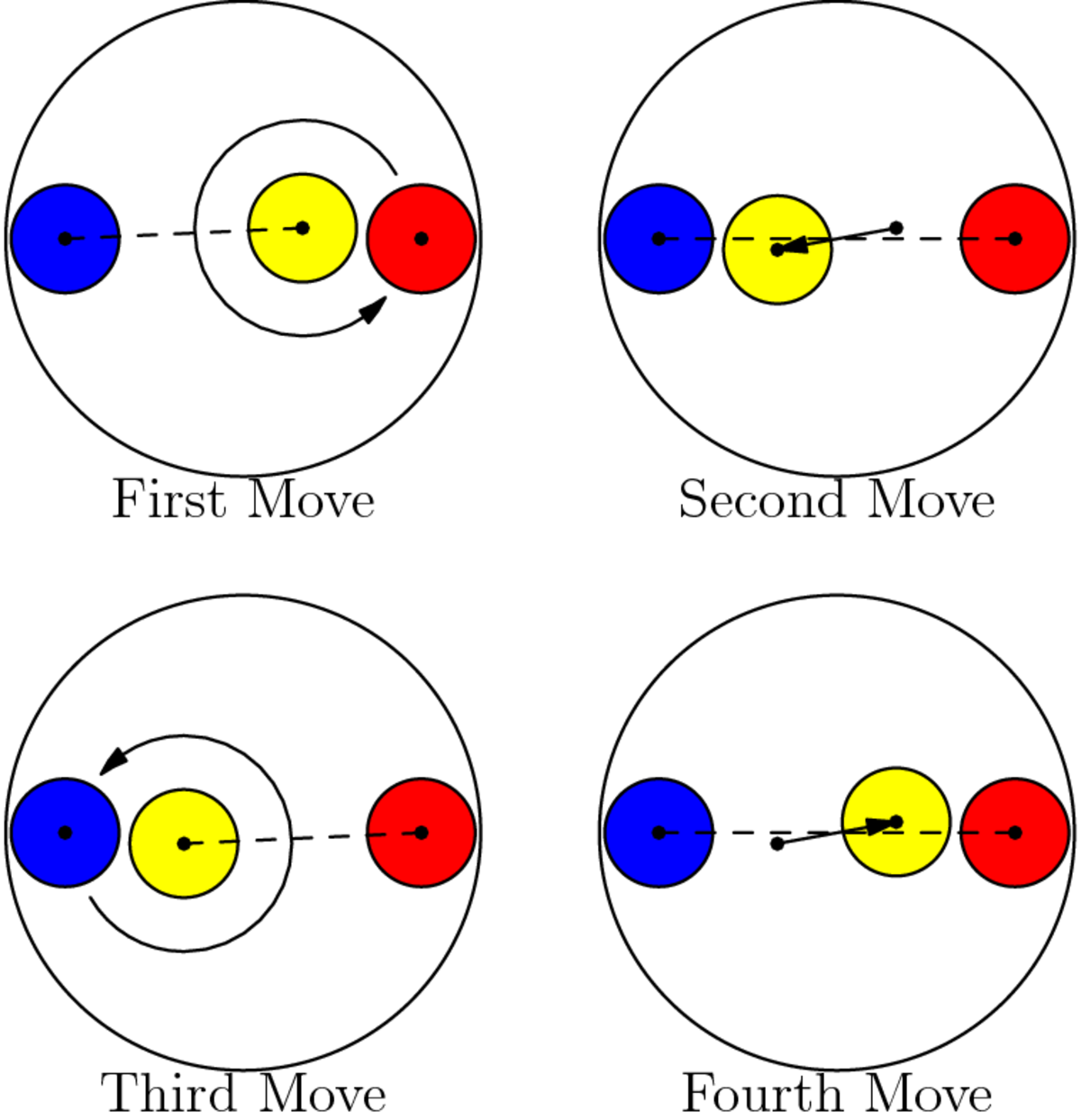
It is not hard to verify that all the geometry makes sense, i.e. initially, the red coin and yellow coin do not overlap, and that on the first move, there is enough room for the red coin to go around the yellow coin, etc., for any ϵ > 0 . Thus, we can obtain a radius arbitrarily close to 4.
Just for the record, I do not know if 4 or smaller is possible.
Log in to reply
Yeah, that's pretty good, Jon, I believe you have managed to shave a tiny bit off my best. Let me think about that and see how tight we can make this. And then we might have to ask the Brilliant staff to change the answer.
The alternative is to further qualify the already-way-long fine print of the provisions to preclude such "bare skirting over the connecting line", but it won't be satisfying to demand an arbitrary figure for just how far past the coin must travel. Let me think about that too.
Log in to reply
@Guillermo Templado Can you explain how you got an answer that is below 4000? Don't worry about being accurate in the approximations, the idea behind going below 4000 could help us see how to minimize this even further.
In the meantime, I've updated the question to ask for Infinium (which includes minimum), and updated the answer to 4000.
Log in to reply
@Calvin Lin – I'm working this wiki , righ tnow. I'm very bussy, and it's a very important wiki for me, because I am finding it really beautiful and I'm going to start the best part... I promise, I'll be back here when I finish there. Leave the answer for 4000, because I don't know how to explain my idea very good and I'm not sure if I'm right. My idea is about tangent circles and the initial position of the 3 coins. My apologies...
Log in to reply
@Guillermo Templado – No worries. Loving the residue theorem wiki :)
Log in to reply
@Calvin Lin – Thank you very much... P.S.- I have been thinking about this problem too, and I don't get to push below 4000. The answer, clearly, can't be less than 3...
I almost agree with you, John, the minimum is able to be an infimum.... and the answer is able to be 4000 or less than 4000..
Log in to reply
How can we push this under 4000?
Log in to reply
@Michael Mendrin – I used Descartes circle theorem twice and I got 3309, if I don't remember bad... I think the answer is a little more of π + 3 ⋅ 0 . 0 1 5 . Don't ask me why?..because, right now, I can't answer you..
Following Guillermo's comments, maybe we should wait to see if anybody else has a proposal to get this under 4. But it does seem to me that any indefinite play is going to involve transversing the line through the centers of two coins twice in at least some moves, once between and once "around the back". Hence, 4 would seem to me to be the absolute minimum.
I still don't know how to best word this problem as not to leave a sour taste in those that have worked on this puzzle.
Edit: Well, there is one way to have the cake and eat it too, and that is to ask for the answer in decimal form. Then people giving the answer of "4.021" or "4.000" will be both marked correct per Brilliant protocol.
Log in to reply
Michael, I think there is "a possible problem" with Jon's solution. The line connecting the centers of the other two coins, is it a segment or a line?.... I think the answer of this problem depends very strong ( of course on the rules) and specially on the inital positions of the 3 coins and rotations (turns). Now, I'm not going to talk until I have a final answer... Right now, I say the solution to this problem is π , but due to I'm not sure, I'll be silent...
I think saying "two children" makes the problem confusing, e.g. having to state in point 5 that they want to actively cooperate. We can just cut it down to a child who is trying to amuse himself with these coins?
Log in to reply
Only because of precedent, see link "Inspiration", etc. But I'll shift the wording around just a bit.
Also, children will do things like that, i.e., playing a game not competitively but collaboratively. I can see how that can be fun, given a large bounded field to play with, seeing what happens with the coins eventually.
Log in to reply
(I like backstabbing games. Cooperative games are tedious lol)
Hm, looking at your solution, it seems like you allow for the path to be curved. If so, this should be made clear. Also, it's not immediately clear that it is a lower bound. Is there a more creative way to play the game that doesn't require cycling back?
My original impression of the problem is that the path is a straight line. I'm basing that on past experience of playing "coin soccer", where you flick one coin between the two of them, towards a goal post. In this case, I can get a radius of 5.000, but don't know it can be reduced.
Log in to reply
@Calvin Lin – Now you understand why the "fine print" in legal papers can be so protracted! I've added further wording to indicate that the kind of path the moved coin takes is arbitrary, and does not have to be a straight line.
As for your comment about "...doesn't require cycling back", it sounds like you'd like to add more to the fine print to block such a dull outcome. Well, as I've already commented, working with larger circular playing fields can get quite amusing, even for children. I'm not sure how to direct this problem to a more interesting outcome, I'll have to think on it.
Really, when you guys at the Brilliant headquarter take time off at the end of the day to go have beers at the local pub, maybe some of you should try playing this game on a slick tabletop.
Log in to reply
@Michael Mendrin – Indeed. I track the fine print of solutions, and help ensure that they are rigorous / complete (or point out the potential concerns).
I'm fine with the cycling back approach that you took. I think that's pretty cute.
My concern is whether or not we could reduce this radius even further by using another moving approach. IE What you have shown is that 4.071 can be achieved, but not shown yet that no smaller value would work.
Log in to reply
@Calvin Lin – I understand your concerns, it's quite difficult to prove this rigorously. At least we know that if there's a smaller possible R , it'll be somewhere between roughly 3 and 4 . But think about one approach to a proof: Whenever a coin passes the line through the centers of the other two coins and does not return back over it (by going around one of the coins), then how is any coin ever going back to that other side of that line? It's easy to see how if the playing field is considerably larger than 4 , but starting with 4 , it's hard to see how.
Very clever solution.
Answer will be 2.96535
The smallest possible circular playing field is the one that has to contain 2 unit circles and 1 circle of radius 3 . Its radius works out to (using Descartes' Circle Theorem )
R = 1 1 3 ( 7 + 1 5 ) = 4 . 0 2 1 6 2 7 2 8 0 . . .
so that the answer is 4 0 2 1
With this arrangement of coins, each turn consists of alternatively moving the left and the right coin at the top down and around the third coin and returning to their original positions. Kind of a boring game if the children played like that, but at least it can be played indefinitely. It's more fun and interesting if the playing field was considerably larger and you're not thinking ahead too much with each move.
Bonus: If all three coins are always in contact with the border of the circular playing field, why will the game always be forced to stop?
Credit for Inspiration goes to Kartik Sharma, who first mentioned this.