Two Circles Puzzle
The two circles in the animation have radii 1 cm and 4 cm , respectively.
How long is the blue curve traced by the blue point on the smaller circle (in centimeters)?
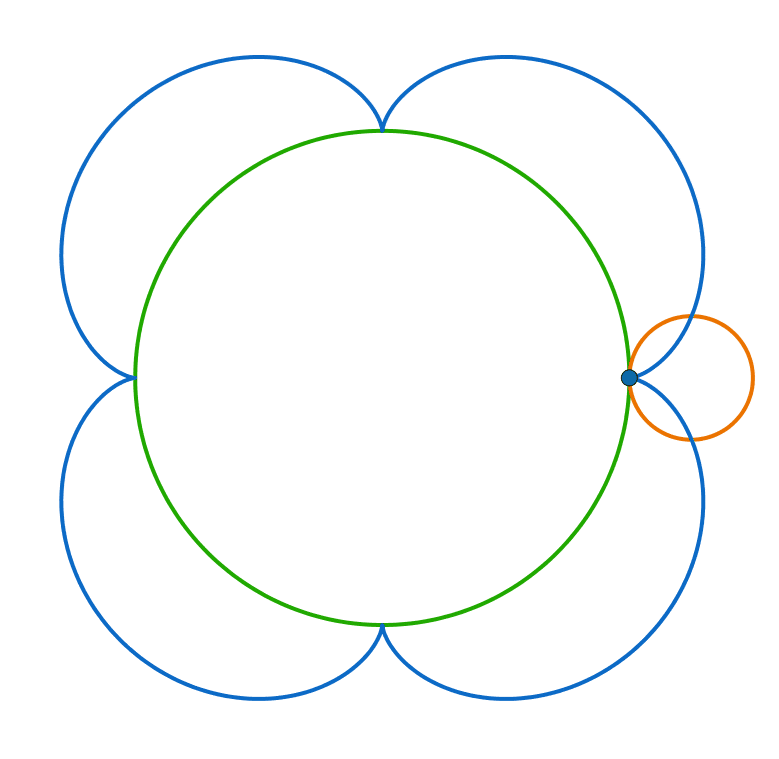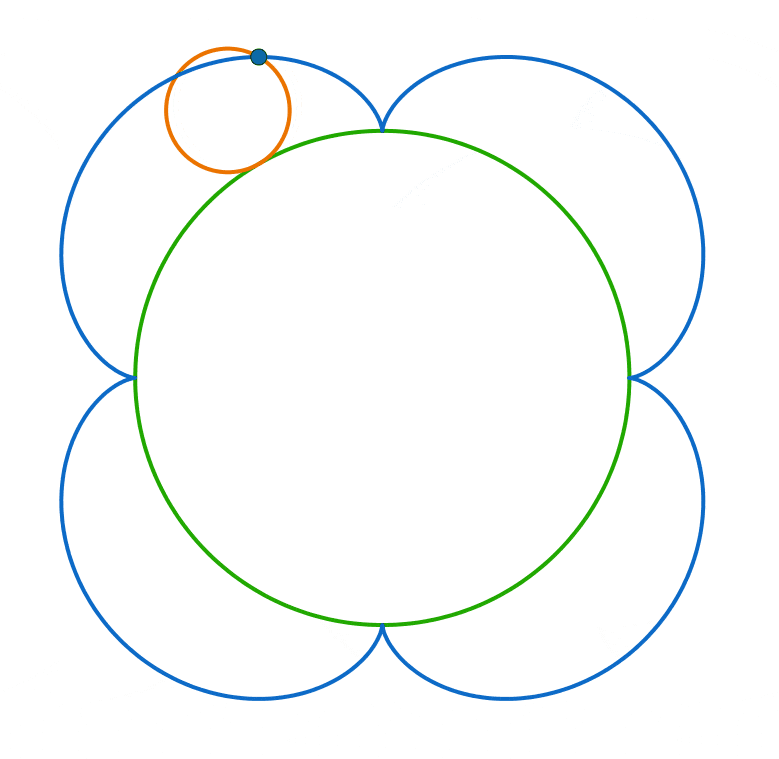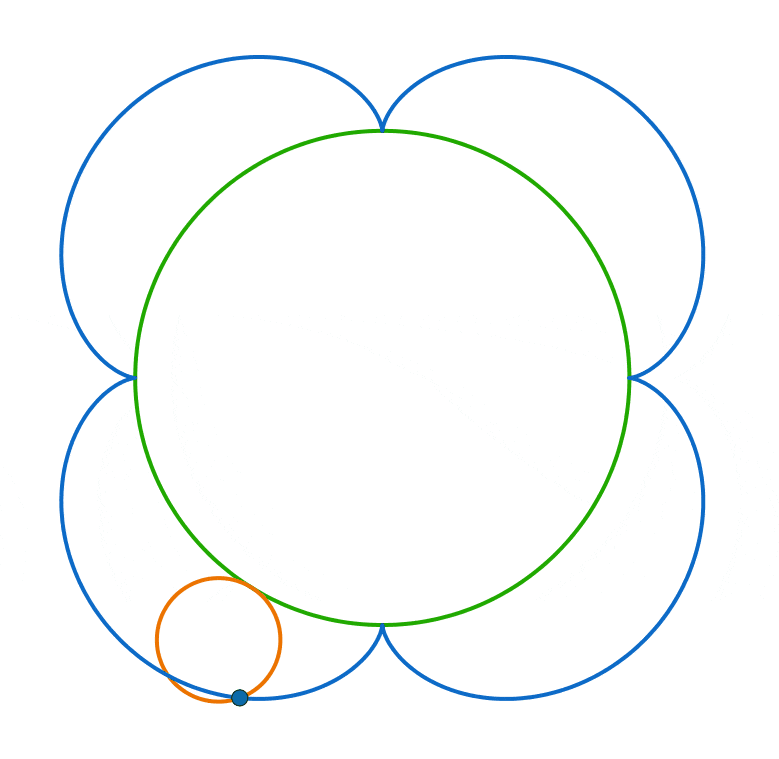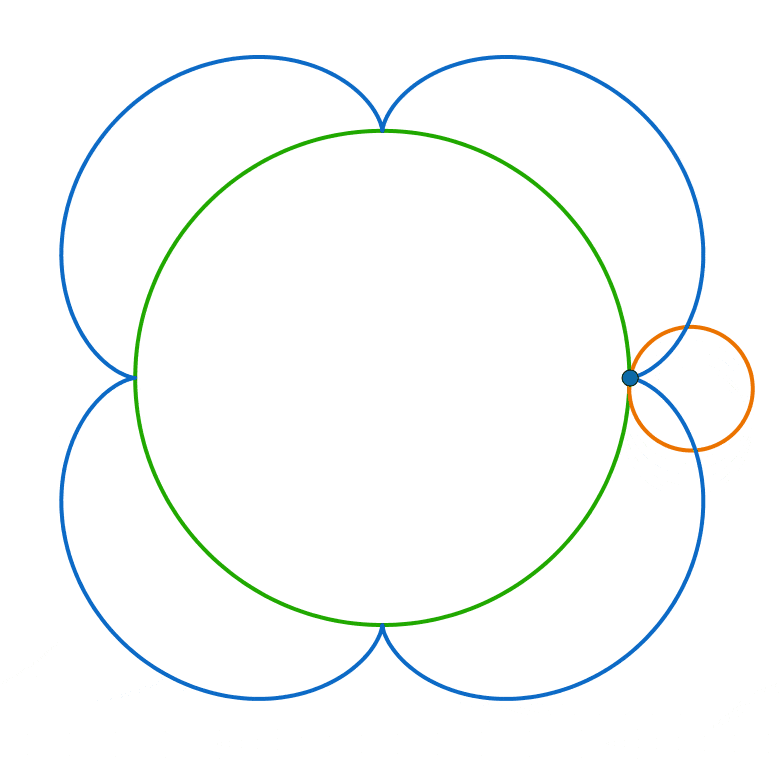
The answer is 40.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
If k = R/r is an integer, the length of an epicycloid arc is L = 8 x r x (R + r), = 8 x 1x (1+4)
Log in to reply
good observation!
Log in to reply
An additional question which can be asked is this:
What is the area enclosed between the epicycloid and the circle.
Log in to reply
@Vijay Simha – Yes, that is a nice problem. Post it! (I may write a solution if I find the time)
@Vijay Simha – If the epicycloid is centered on the origin, this integral would give the area within the arc in the first quadrant, using the parametric equations for the epicycloid given in the solution:
∫ π / 2 0 ( 5 sin ( x ) − sin ( 5 x ) ) ( − 5 sin ( x ) + 5 sin ( 5 x ) ) d x
This comes out to equal 2 1 5 π . We subtract the area of the quarter circle in the first quadrant, 4 π , and then multiply by four to get 1 4 π c m 2 as the total area between the larger circle and the epicycloid.
Log in to reply
@Joseph Jennings – Yes, that is a nice application of Green's Theorem.
Isn't Simha's formula dimensionally inconsistent? Should it not be 8X(R+r) if k is an integer?
Isn't your formula dimensionally inconsistent? Should it not be 8X(R+r) if k is an integer?
Log in to reply
Yes, indeed! The arc length of one "petal" is R 8 r ( R + r ) . If r R happens to be an integer, as in our example, the total length of the closed curve comes out to be 8 ( R + r ) .
(Playing devil's advocate) What is wrong with the following logic:
The small circle traces the path 4 times. Hence, the perimeter is 4 × 2 π × 1 = 8 π .
Log in to reply
That’s the way I looked at it first but then I noticed that that answer is the same as the circumference of the large circle so it can’t be correct.
Since the smaller circle is rolling on the larger, the arc lengths X P and X A must be the same length. Thus, if ∠ X O A = t , then ∠ X B P = 4 t .
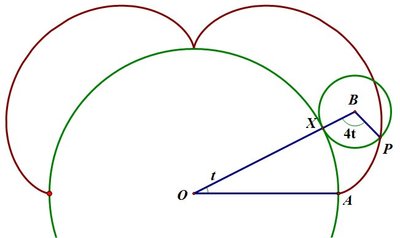
Thus O P = ( 5 sin t 5 cos t ) − cos 4 t ( sin t cos t ) − sin 4 t ( cos t − sin t ) = ( 5 sin t − sin 5 t 5 cos t − cos 5 t )
Otto, I’m struggling with “small circle will revolve five times”. I have stared at the dot for ages and I still only see four revolutions. My reasoning (which may be incorrect): the large circle has a radius four times the radius of the small circle so it has a circumference four times that of the little circle. If the small circle rolls along a path that is four times its own circumference, then it will roll four times, not five. I’m obviously missing some thing and getting frustrated. Can you please advise?
Log in to reply
Pay attention to one of the four "petals," perhapst the "first," on the top right. As it travels through this petal, the moving circle will rotate not 3 6 0 o but 450.The highlighted dot is initially on the left but at the bottom at the end, having made one revolution and then an additional quarter. Hope that helps; please let me know.
Start with the red circle at the top of the picture. At that moment the blue dot is at the bottom of the red circle. Now count how many times the blue dot returns to the bottom of the circle. The red circle gets to the top of the picture on the fifth return of the blue dot. (The animation is a little fast to follow this, but after a few tries at counting one gets it.)
Log in to reply
Thanks Dennis and Otto, I can see now that the small circle rotates five times. The maths after that is way beyond me but it is interesting see how you got to the solution: by determining the speed of the dot and from that determining the distance travelled. And I see that my description of the small circle rolling along a line that is four times its circumference doesn’t work when that line isn’t a straight line. But I really am out of my depth with this question.
Thanks ! I was struggling too and this helped ! Just in case anyone stuck the same way as me. Do not reference the x-axis with circumference of the big (green) circle. Then count as Dennis stated. I do this by imagining moving a straight line moving up and down touching the bottom of the small (red) circle.
Log in to reply
@Entropy Uncertainty – A similar "confusing" situation. The earth goes once round the sun in one year of 365.25 days. These are "solar" days, the time from one midday (facing the sun) to the next. But in that year the earth has actually rotated 366.25 times relative to the other stars in the sky.
If the big circle were a straight line then it would rotate 4 times, but not so on a circle. Think about the point half way around the big circle. The point on the small circle is at the other side from where it started, so it's already half way to completing an additional revolution.
Can someone explain the trig used to get the velocity? I got the equations for x and y and manged to get the answer by integrating sqrt((dx)^2 + (dy)^2) dt which turned into sqrt(41 + 40cos4t) dt but I had to put the integral into wolfram. So I'd like to know that step.
Log in to reply
I believe the speed is 5 0 − 5 0 cos ( 4 t ) ; now use the double-angle formula, cos ( 4 t ) = cos 2 ( 2 t ) − sin 2 ( 2 t ) = 1 − 2 sin 2 ( 2 t ) .
I thought of using the cycloid arc length equation (just open the big circle and make it a straight line), but since for me there were only 4 revolutions of the blue dot I tried 32 (the equation for length on the cycloid is 8a, where a = radius of the small circle), but that didn't work. With your comment I realised that the blue dot actually does 5 revolutions and not 4. Thanks.
The small circle center traces a circular path with radius 5 cm therefore with length equal to 2 ⋅ π ⋅ 5 c m Because the small circle perfectly rotates without skidding, for the center of the small circle to travel that much the latter needs to rotate 5 times since per rotation its center travels 2 ⋅ π ⋅ 1 c m .
Knowing that per rotation the length of the cycloid traced by a circle with radius r is equal to 8 r , then for 5 rotations the path length will be 5 ⋅ 8 ⋅ r = 5 ⋅ 8 ⋅ 1 c m = 4 0 c m .
Log in to reply
Wow, P S! After seeing the previous correct answers that were so complex that I was left dismayed, here is another correct answer that does not resort to trigonometry nor calculus. Put that way, it is so simple. Bravo!
If R= (m - 1)r, where r=1 and m=5 in this example, then the length of the epicycloid = 8mr, therefore,
Answer=40
Why is it not 8pi?
I like to have an angle of 0 at the positive x-axis, and start at the tip of a petal, so I have the picture turned over 45°. The center of the orange circle makes a circular motion around the origin, which can be parametrized as (x,y) = 5(cos t, sin t). In the same time, the orange circle makes 5 full circles (4 and an additional one for the revolution). The net motion of the blue dot is described by x = ( 5 cos t + cos 5 t , 5 sin t + sin 5 t ) . The velocity then is given by the time derivative: the vector v = 5 ( − sin t − sin 5 t , cos t + cos 5 t ) . The speed then is ∣ v ∣ = 5 sin 2 t + 2 sin t sin 5 t + sin 2 5 t + cos 2 t + 2 cos t cos 5 t + cos 2 5 t = 5 1 + 2 sin t sin 5 t + 2 cos t cos 5 t + 1 = 5 2 1 + cos 5 t cos ( − t ) − sin 5 t sin ( − t ) ) = 5 2 1 + cos ( 5 t − t ) = 5 2 1 + cos 4 t using sin ( − t ) = − sin ( t ) and cos ( − t ) = cos ( t ) .
Integrating the speed over time gives the distance traveled:
L = 5 2 ∫ 0 2 π 1 + cos 4 t d t . Set x = 4 t and use the range where sin is nonnegative:
5 2 ∫ 0 8 π 1 + cos x 4 d x = 4 8 × 5 2 ∫ 0 π 1 + cos x d x
And ∫ 1 + cos x d x = 2 1 − cos x on the interval [ 0 , π ]
So our expression is L = 1 0 2 ( 2 1 − − 1 − 2 1 − 1 ) = 4 0
Having been told the answer was an integer. I carefully drew the shape and examined its length I got 39.91 so the answer was 40.
Perhaps this problem is easier than I thought.
This kind of shape is called an epicycloid .
Let's say we have an epicycloid whose static circle has radius a and whose turning circle has radius b .
To find the general expression for the epicycloid, consider the movement of the moving circle. Its center goes around another circunference with radius a + b , and along the movement the smaller circle completes b a rotations corresponding to each curve "petal" plus one full rotation around the static circle, in a total of b a + b laps.
We can then write the parametric formula as:
P ( t ) = ( x ( t ) , y ( t ) ) = ( ( a + b ) cos t − b cos ( b a + b t ) , ( a + b ) sin t − b sin ( b a + b t ) ) , t ∈ [ 0 , 2 π ]
Consider a tiny segment of the curve, short enough we can approximate it as a line segment. We've Δ s 2 = Δ x 2 + Δ y 2 .
So we can find the derivative of P with respect to both x and y and integrate using the above formula to find the total perimeter of the curve.
( P x ˙ , P y ˙ ) = ( − ( a + b ) sin t + ( a + b ) sin ( b a + b t ) , ( a + b ) cos t − ( a + b ) cos ( b a + b t ) )
s ˙ ( t ) 2 = P x ˙ 2 + P y ˙ 2 = ( a + b ) 2 ( ( sin 2 t + cos 2 t + sin 2 ( b a + b t ) + cos 2 ( b a + b t ) ) − 2 ( sin t cos ( b a + b t ) + sin t sin ( b a + b t ) ) )
s ˙ ( t ) 2 = 2 ( a + b ) 2 ( 1 − cos b a t )
s ˙ ( t ) 2 = 4 ( a + b ) 2 sin 2 ( 2 b a t ) since 2 sin 2 t = 1 − cos 2 t
⟹ ∣ s ˙ ( t ) ∣ = 2 ( a + b ) ∣ sin ( 2 b a t ) ∣
∫ 0 2 π ∣ s ˙ ( t ) ∣ d t = 2 ( a + b ) ∫ 0 2 π ∣ sin ( 2 b a t ) ∣ d t = 2 ( a + b ) ( b a ) ∫ 0 a 2 π b sin ( 2 b a t ) d t = 2 ( a + b ) ( b a ) ( a 4 b ) = 8 ( a + b )
Since a + b = 5 , the answer is 4 0
Trig identities are the hard part. Again...
The center of the small circle will move along a circle of radius 5, and the small circle will revolve five times as it moves once around the large circle. (One might at first expect that the small circle revolves four times; but watch the dot carefully!) Thus we can parameterize the "blue curve" as x = 5 cos ( t ) − cos ( 5 t ) and y = 5 sin ( t ) − sin ( 5 t ) for 0 ≤ t ≤ 2 π . Using a bit of trigonometry, we find the speed to be v = 1 0 ∣ sin ( 2 t ) ∣ , and the arc length is L = ∫ 0 2 π 1 0 ∣ sin ( 2 t ) ∣ d t = 4 0 c m .