Two identical Inductor

A circuit has two identical inductors, two identical voltmeters A and B and a source of alternating voltage v ( t ) = V 0 sin ( 2 π f t ) .
The voltmeters offer only resistances in the circuit. If the frequency of the voltage source is changed over a wide range, and the maximum reading the voltmeter B shows is α V 0 , find α .
Hint: Use phasor diagram.
The answer is 0.333.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Chew-Seong Cheong
I surprised you used AM-GM. It is really a useful tool.
By the way, how you write that blue line besides your solution for explaining something?
Log in to reply
Hope the following helps. By the way, I have changed the last part of your problem question. Because it did not ask to submit α as answer.

Log in to reply
@Chew-Seong Cheong Thank you so much for sharing
@Lil Doug , I have changed the figure for you. I used Paint to do it.
Log in to reply
@Chew-Seong Cheong Thanks this figure is really cool.
Let the resistance of the voltmeter be 1 . The choice of resistance value does not affect the max value of V B , even though it does affect the value of inductive reactance at which it occurs.
Define the series and parallel R L impedances as follows:
Z S = 1 + j X Z P = 1 + j X j X
Then the voltage across voltmeter B is:
V B = V 0 Z S + Z P Z P = V 0 ( 1 + j X ) 2 + j X j X
The magnitude of this quantity is:
∣ V B ∣ = V 0 1 + 7 X 2 + X 4 X
Differentiate the above expression with respect to X and set it to zero to find the max value. The maximum value of V B is 3 1 V 0 when X = 1 .
@Steven Chase what is the meaning of S and P?
Log in to reply
Z S is the impedance of the series RL branch, and Z P is the impedance of the parallel RL branch
@Steven Chase can I interchange the values of Z S and Z P ?
Log in to reply
I would not make that assumption
Log in to reply
@Steven Chase W H Y ?
Log in to reply
@Talulah Riley – There is no reason to think that they should be the same
Log in to reply
@Steven Chase – @Steven Chase ok noted. Why the resistance of inductor is imaginary only?
Log in to reply
@Talulah Riley – Because the current and voltage for an inductor are 90 degrees out of phase with each other. This corresponds to an impedance of the form Z = j X
Log in to reply
@Steven Chase – @Steven Chase I didn't understand this sentence physically
Log in to reply
@Talulah Riley – You can refer to this note
https://brilliant.org/discussions/thread/lc-impedance-conventions/?ref_id=1601272
@Steven Chase
Hello. Please help me in this problem
Thanks in advance.
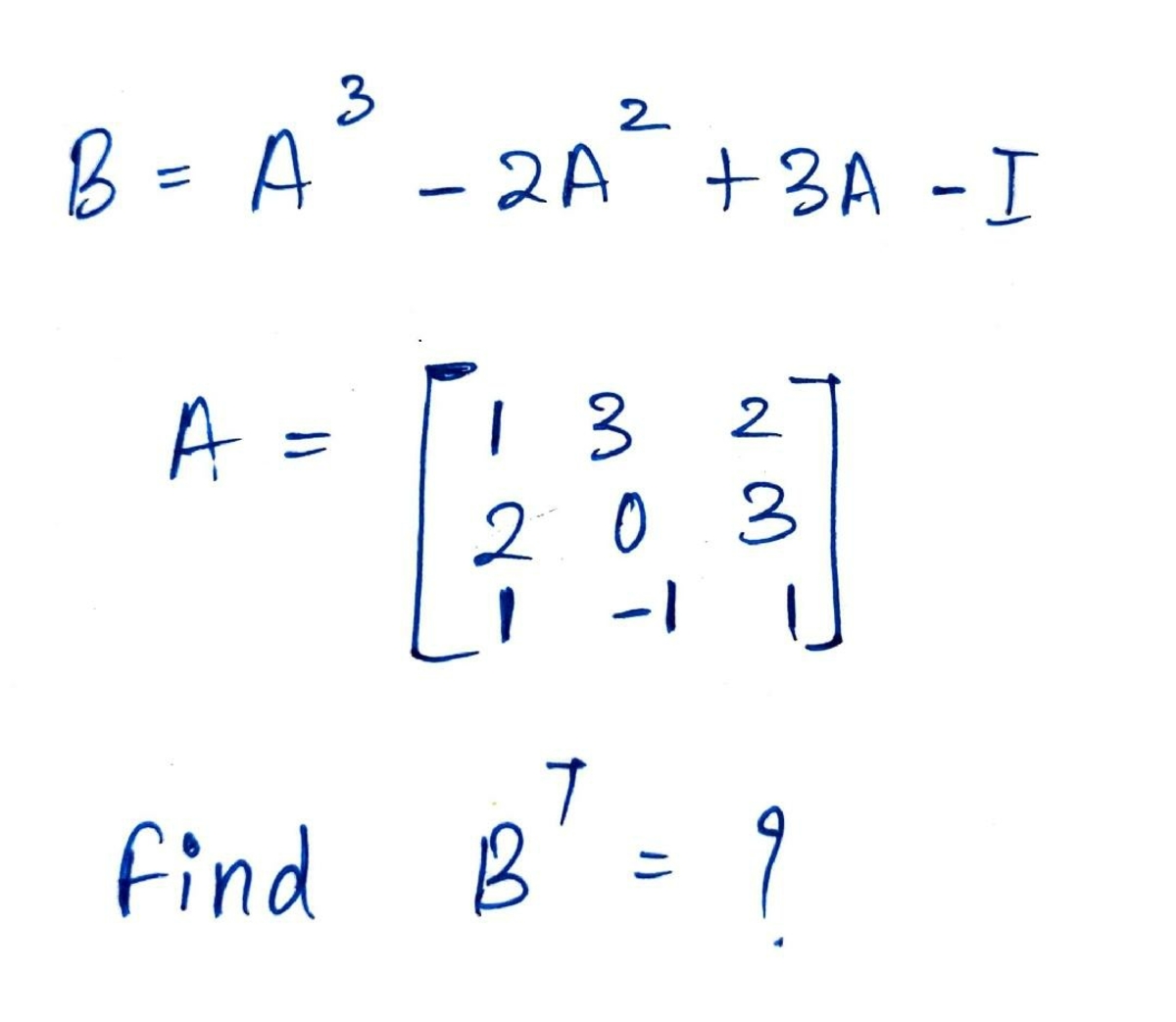 Hope I am not disturbing you.
Hope I am not disturbing you.
Log in to reply
Hello. If you know how to multiply matrices, this one is straightforward, but tedious. Perhaps there is some fancy way of finding the answer without doing the multiplications, but I don't know what it is.
Nice solution.
Log in to reply
Agreed, thanks for pointing that out. I have amended the solution. The analytical derivation was actually just an afterthought, because people like to see such derivations. I initially solved the problem by writing code and doing a numerical sweep. The code solution doesn't require explicit derivation of that expression.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
|
Let the resistance of the voltmeters be R , the inductance of the inductors be L , and 2 π f = ω . Then the reading on voltmeter B is:
V B = R + j ω L + R + j ω L j ω R L R + j ω L j ω R L = ( R + j ω L ) 2 + j ω R L j ω R L = R 2 − ω 2 L 2 + 3 j ω R L j ω R L = 3 + j ω R L ω 2 L 2 − R 2 1
⟹ ∣ V B ∣ = ∣ ∣ ∣ 3 + j ω R L ω 2 L 2 − R 2 ∣ ∣ ∣ 1 = 3 2 + ( ω R L ω 2 L 2 − R 2 ) 2 1 = R 2 ω 2 L 2 + 7 + ω 2 L 2 R 2 1 ≤ 2 + 7 1 = 3 1 ≈ 0 . 3 3 3 By AM-GM inequality: R 2 ω 2 L 2 + ω 2 L 2 R 2 ≥ 2 Equality occurs when R = ω L
Reference: AM-GM inequality