Two Inductors - Part 2
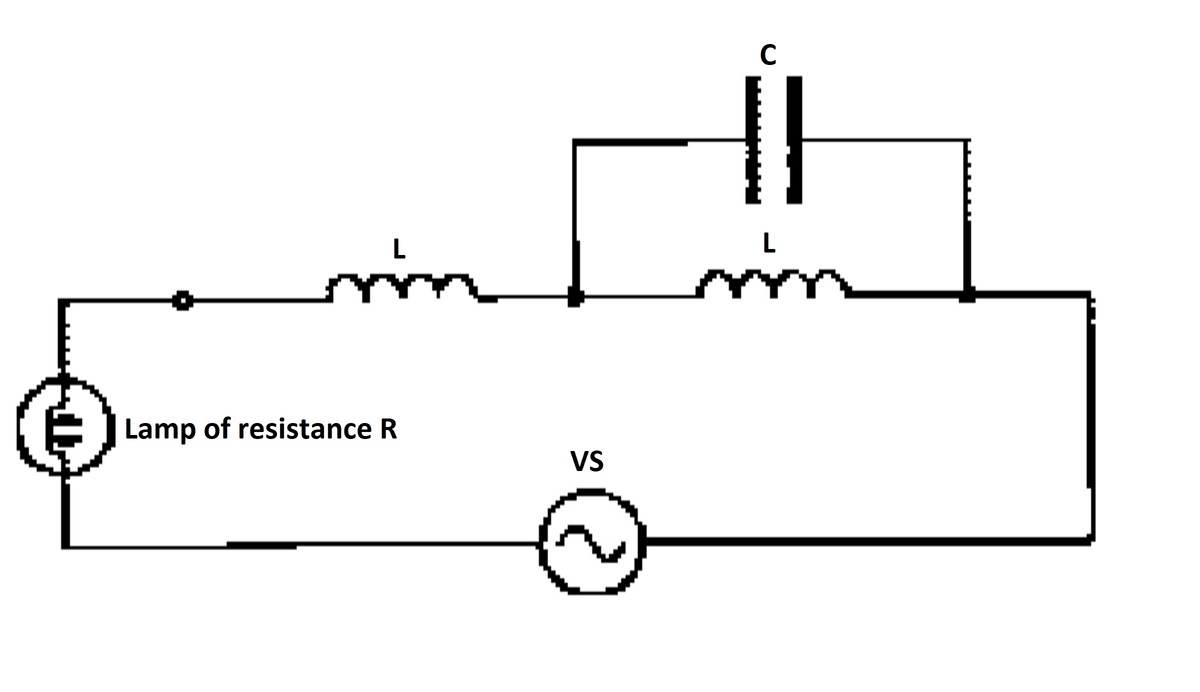
An AC voltage source supplies a system consisting of a resistive lamp, two identical inductors, and a capacitor. At time t = 0 , the inductors and capacitor are de-energized.
How much heat energy is dissipated in the lamp from t = 0 to t = ∞ ?
Details and Assumptions:
1)
V
S
=
1
0
cos
(
t
)
2)
R
=
L
=
C
=
1
The answer is 50.0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Lil Doug @Krishna Karthik In case you're interested
Log in to reply
Hmm. Nice one (upvoted). Would t <= 1000 be unecessary?
Thanks for sharing. While solving, I did wonder why the current dissipates and rechecked my work, especially since I performed some manipulations where it is easy to err. Turns out the reasoning you've laid out in your solution applies. Nice problem.
Log in to reply
@Karan Chatrath can I ask you a integration doubt now?
@Steven Chase why did time is t < = 1 0 0 ?
Log in to reply
Perhaps you can take a guess
Log in to reply
@Steven Chase
If I guess then 100 is a very large time, so upto that time the heat dissipated by the resistor is carried on.
Log in to reply
@Talulah Riley – Yeah, that is right. The program can't deal with infinity, so I had to choose a fairly large finite number
Log in to reply
@Steven Chase – @Steven Chase But my software is coming which can choose ∞ , we have also talked about this before. :)
Log in to reply
@Talulah Riley – But it's impossible. Programming is an exact science that deal with exact values; we can't deal with limits like infinity in programming.
Maybe artificial intelligence can solve it that way, by using traditional limit solving, but not traditional programming.
Usually, for infinity, your calculators deal with 1 0 − 9 9 9 or some value like that for negative infinity. Sadly, it's an impossibility in computer programming.
@Steven Chase can I ask you a integration doubt?
Log in to reply
Sure. I'm not the best at doing integrals by hand though
@Steven Chase @Karan Chatrath can you please help me in this to solve it analytically ∫ ( 1 6 + 9 sin x ) 2 1 d x , Thanks in advance
Log in to reply
It's extremely difficult. I got a huge-ass answer from an integral calculator. I used Weirstrass substitution before I gave up; the integral calculator gives an extremely long answer.
@Lil Doug I've posted a new note for your integral
Let the current through the resistor be I , that through the parallel inductor be I 2 and that through the capacitor be (I_1)
Charge on the capacitor is Q 1
Circuit equations:
− V S + I + I ˙ + I ˙ 2 = 0 I 1 + I 2 = I Q ˙ 1 = I 1 Q 1 = I ˙ 2
I ( 0 ) = I 1 ( 0 ) = Q 1 ( 0 ) = I 2 ( 0 ) = 0
Manipulating and rearrangine the differential equations to obtain an ODE governing I yields:
d t 3 d 3 I + d t 2 d 2 I + 2 d t d I + I = 0
I ( 0 ) = 0 I ˙ ( 0 ) = 1 0 I ¨ ( 0 ) = − 1 0
This final ODE is solved numerically. The resulting heat dissipated can be computed as such (also done numerically):
H = ∫ 0 ∞ I 2 R d t H ≈ 5 0
I have typed out a solution but I seem to have run into the problem you recently highlighted regarding latex.
I am not deleting this as of now.
Log in to reply
Nice one bro.
Woah... that was a third order equation. Niiiice...
Log in to reply
@Krishna Karthik i mentioned you for another thing, that was a bug here.
@Karan Chatrath delete it, what are you waiting for??
Log in to reply
I have updated it, but I have left out intermediate steps. You can try it yourself now.
Log in to reply
@Karan Chatrath how did you solved that 3rd order equation?
Log in to reply
@Talulah Riley – It's solved numerically, using Explicit Euler (it's kind of hard to implement using Runge-Kutta 4; Runge Kutta has some interdependencies between variables that makes it really hard with the order of what to code it in). It's slightly more computationally expensive than your standard second order differential equation.
It goes like this:
d t 3 d 3 I = − I ¨ − 2 I ˙ − I
I ¨ = I ¨ + d t 3 d 3 I d t
I ˙ = I ˙ + I ¨ d t
I = I + I ˙ d t
There are three main operations here; extrapolating the second derivative, the first derivative, and finally, the actual value of the current.
That's why it's going to be much less accurate. However, there are already solvers programmed for 3rd order differential equations.
@Karan Chatrath you can post solution using pen and page, that's the simple and traditional way.
@Karan Chatrath i want laplace solution only. Because I want to learn it.
@Karan Chatrath
sorry. I want to apologize. Please forgive me.
I was little bit , excited regarding Laplace of this solution.
And in solution you said I used numerical route, which little bit hurt me.
Log in to reply
It is okay.
Using Laplace here will not be useful as the characteristic equation of the current is a third degree polynomial. So performing an inverse Laplace transform is not trivial.
Log in to reply
@Karan Chatrath
But the solution which you posted before,
I was trying to decode that, somewhere I read (taking laplace both sides)
So?
Log in to reply
@Talulah Riley – Yes, initially I operated in the Laplace domain but because of the third-order polynomial, I had to switch back to the time domain. That made me realise that Laplace transformation is not very useful in this case.
Log in to reply
@Karan Chatrath
–
@Karan Chatrath
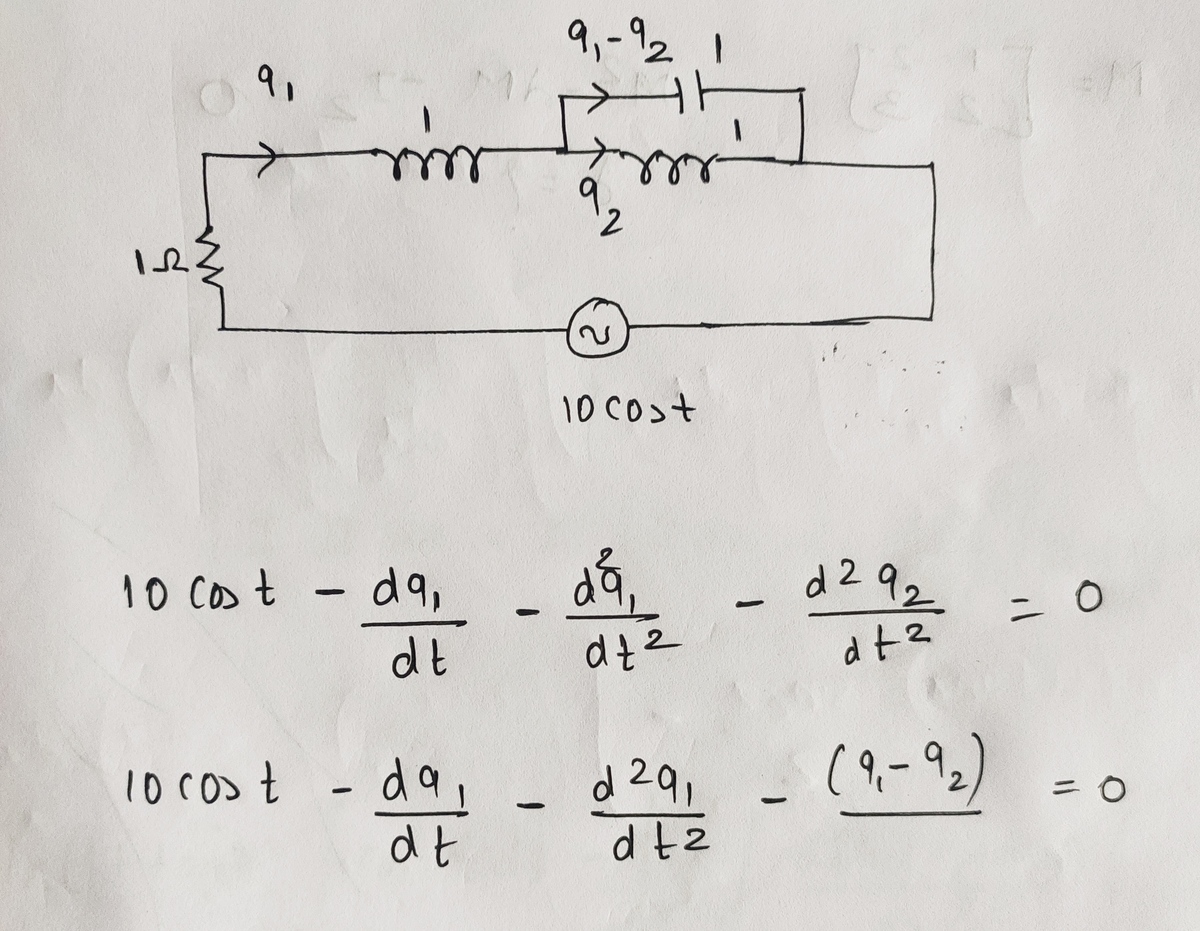
i started solving this way
I tried to solve this pair of differential equation in worlfram, but wolfram failed
My solution is similar to that of @Karan Chatrath, but with some stylistic differences. Recall from the previous problem that when the applied angular frequency is L C 1 , the parallel L C branch has infinite impedance in AC steady-state. Consequently, current only flows in the circuit during an initial transient phase, which eventually dies out. This is why it is reasonable to propose that the energy dissipated in the lamp over infinite time is finite.
The state variables are the inductor currents and the capacitor voltage.
Fundamental equations:
V L 1 = L 1 I ˙ L 1 V L 2 = L 2 I ˙ L 2 I C = C V ˙ C
Write the left sides in terms of other state variables.
V S − R I L 1 − V C = L 1 I ˙ L 1 V C = L 2 I ˙ L 2 I L 1 − I L 2 = C V ˙ C
All that remains is to isolate the derivative terms and numerically integrate. The energy dissipated in the lamp is:
E l a m p = ∫ 0 ∞ I L 1 2 R d t
In practice, all we have to do is integrate over a large finite time span.