Two many

${x}^{2}-{2}^{x}=0 \quad \Leftrightarrow \quad {x}^{2}={2}^{x}$

A common mistake is to think there are only one or two solutions ( $x=2,4$ ). However we see there is a third solution by sketching the graphs $y={x}^{2}$ and $y={2}^{x}$ on the same axes.

At $x=0$ , ${x}^{2}=0$ and ${2}^{x}=1 \Rightarrow {x}^{2}<{2}^{x}$ .

At $x=-1$ , ${x}^{2}=1$ and ${2}^{x}=\dfrac 12 \Rightarrow {x}^{2}>{2}^{x}$ .

As both graphs are continuous, they must cross over each other in the interval $(-1,0)$ , and we find the third and final solution there.

As $x$ tends towards $-\infty,$ $x^2$ tends towards $\infty$ and $2^x$ tends towards $0.$ So $x^2>2^x$ for sufficiently large negative $x.$ As $x$ tends towards $+\infty,$ both functions tend towards $\infty,$ but $2^x$ grows at a faster rate. $\lim_{x\rightarrow\infty}\frac{2^x}{x^2}=\lim_{x\rightarrow\infty}\frac{\ln2\times2^x}{2x}=\lim_{x\rightarrow\infty}\frac{(\ln2)^2\times2^x}{2}=\infty$ So $2^x>x^2$ for sufficiently large positive $x.$

This means that the graphs of $y=2^x$ and $y=x^2$ cross $1+2k$ times for some integer $k,$ unless the graphs are tangent to each other at any points (some elementary calculus tells us that they are not). We already know of the solutions $x=2$ and $x=4,$ so there must be at least one more to make the number of solutions an odd number.

The graph of $y=x^2$ is concave up and decreasing when $x<0.$ Thus, if there exists an $x$ -value $n<0$ where $2^n<n^2$ locally to the left of $n$ and $2^n>n^2$ locally to the right of $n,$ then this solution is the minimum solution. We see that at $x=0,$ $2^x=1$ and $x^2=0,$ and that at $x=-1,$ $x^2=1$ and $2^x=\frac{1}{2},$ so by the Intermediate Value Theorem, there exists a solution in $(-1,0).$ This is our third solution.

another method

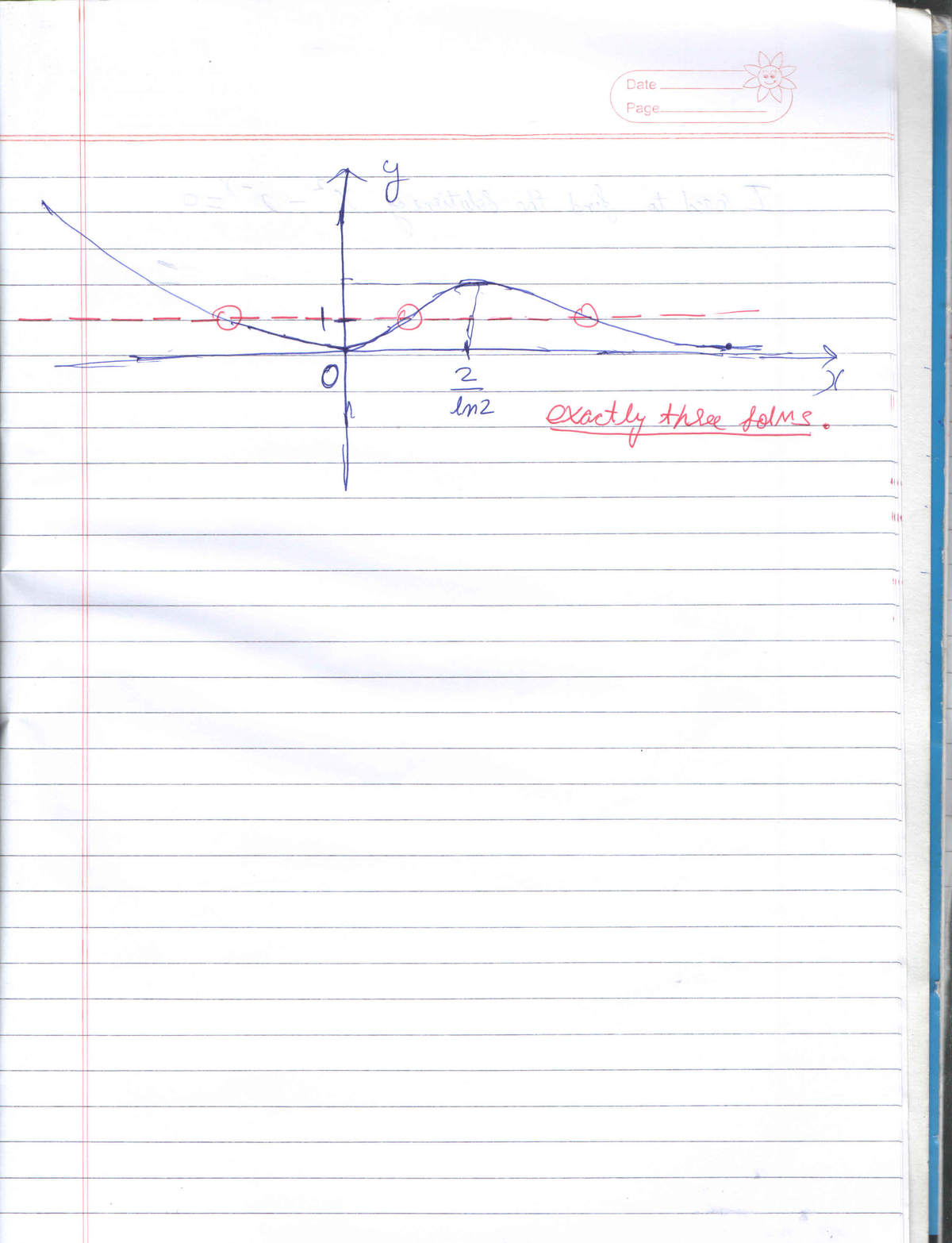
The above is used to draw a rough sketch of f(x) that is shown below :-

from calculator we can see that f(2/ln2) >1

and draw y=1 line to see that it cuts f(x) at exactly 3 points

graph

Simply plot a graph for the given equation and see at how many places does the plot cross the x-axis (ie ordinate is zero)

X^2 = 2^X or 2 ln(X) = X ln(2) If X=2k then 2 (ln2k) = 2k ln(2) or 2 k ln(2) = 2^k ln(2), cancelling ln(2) yields 2 k = 2^k which is valid for k=1 and k=2 which yields X=2^1 =2 and X = 2^2 = 4 for X>0

At X>4, 2^X is greater than X^2, both will approach infinity.

At 2<X<4, X^2 is greater than or above 2^X.

At 0<X<2, X^2 is less than or below 2^X.

For X<0, X^2 will increase to infinity while 2^X will approach 0 asymptotically so 2^X will again intersect X^2 at a point and be less than or fall below X^2 at some point in X<0 which may be solved numerically or graphically as X=-0.766665.

Thus there are three (3) real solutions for X^2=2^X, two positive and one negative.