Two Parabolas and an Equilateral Triangle
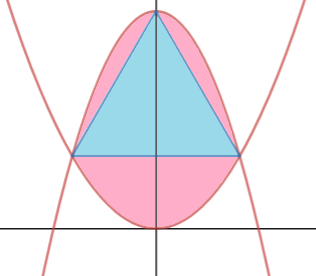
An equilateral triangle has a base that is parallel to the x -axis, two vertices on the parabola y = x 2 , and all three vertices on another parabola that opens downward, as pictured.
If the area of the equilateral triangle is equal to the area of all the regions between the parabolas and the triangle, then the y -coordinate of the vertex on the y -axis is b a , where a and b are positive co-prime integers. Find a + b .
The answer is 13.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions

I guess that this is the intutive approach. I also used this approach to solve the problem with slightly different algebraic manipulation. Guess basically everyone who solved the problem is doing it this way, while others are using the fact that 2/3 of the area of the rectangle is the area enclosed by two parabolas.
Let P ( p , p 2 ) be the rightmost vertex and Q be the topmost vertex of the equilateral triangle, and draw a box outlining the regions between the parabola and the equilateral triangle.
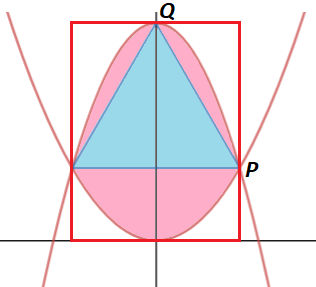
Then the side of the equilateral triangle is 2 p , so its height is 3 p , and its area is A △ = 4 3 ( 2 p ) 2 = 3 p 2 .
Since P has a y -coordinate of p 2 and the height of the equilateral triangle is 3 p , the coordinates of Q are ( 0 , p 2 + 3 p ) . This makes the area of the outlining box A b o x = 2 p ( p 2 + 3 p ) .
Since the area of the equilateral triangle is equal to the area of all the regions between the parabola and the triangle, and the area of the regions between the parabolas (including the equilateral triangle) is 3 2 the area of the outlined box, 3 2 A b o x = 2 A △ or 3 2 2 p ( p 2 + 3 p ) = 2 3 p 2 , which solves to 2 3 .
Therefore, the y -coordinate of the vertex on the y -axis is p 2 + 3 p = ( 2 3 ) 2 + 3 ( 2 3 ) = 4 9 , so a = 9 , b = 4 , and a + b = 1 3 .
How did you get 3 2 ?
Log in to reply
It's a theorem about areas of parabolas. From Wikipedia : "If the chord has length b , and is perpendicular to the parabola's axis of symmetry, and if the perpendicular distance from the parabola's vertex to the chord is h, the parallelogram is a rectangle, with sides of b and h . The area, A , of the parabolic segment enclosed by the parabola and the chord is therefore A = 3 2 b h "
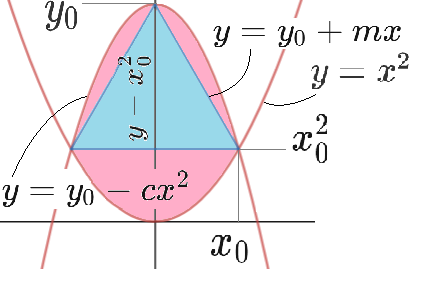
We want to find y 0 .
There are four unknown constants: { x 0 , y 0 , c , m } . To determine y 0 , we therefore need to find four restrictions. These will be (1) the 6 0 ∘ angle of the equilateral triangle, (2) the intersection of the parabolae at x = x 0 , (3) slope = run rise , and (4) the equivalence of the pink and blue areas.
- x 0 y 0 − x 0 2 = tan 3 π = 3 x 0 2 + 3 x 0 − y 0 = 0 ( Note that x 0 2 = y 0 − 3 x 0 . ) x 0 = 2 − 3 ± 3 + 4 y 0 = 2 3 + 4 y 0 − 3 ( x 0 > 0 )
- y 0 − c x 0 2 = x 0 2 c = x 0 2 y 0 − x 0 2 = x 0 ( x 0 y 0 − x 0 2 ) = x 0 3
- m = x 0 x 0 2 − y 0 = − 3
- 2 1 ( 2 x 0 ) ( y 0 − x 0 2 ) = 2 ∫ 0 x 0 y 0 − c x 2 − ( y 0 − 3 x ) + x 0 2 − x 2 d x x 0 ( y 0 − x 0 2 ) = 2 ∫ 0 x 0 x 0 2 + 3 x − ( 1 + c ) x 2 d x = 2 [ x 0 3 + 2 3 x 0 2 − ( 1 + x 0 3 ) 3 x 0 3 ] y 0 − x 0 2 = ( 2 − 3 2 ) x 0 2 + 2 3 ( 2 1 − 3 1 ) x 0 y 0 − 3 3 x 0 = 3 7 x 0 2 = 3 7 ( y 0 − 3 x 0 ) 3 4 y 0 = 2 3 ( 2 3 + 4 y 0 − 3 ) 3 4 y 0 + 3 = 9 + 1 2 y 0 9 1 6 y 0 2 + 8 y 0 + 9 = 9 + 1 2 y 0 y 0 ( 9 1 6 y 0 − 4 ) = 0 y 0 = 4 9 ( y 0 = 0 )
Let the equation of the second parabola be y=k-b(x^2), such that it's vertex is at (0,k). The two paraboli meet at [√{k/(b+1)}, k/(b+1)]. Then the length of the side of the equilateral triangle 'a' is given by a^2=[k/(b+1)]+[bk/(b+1)]^2=4k/(b+1). By the given condition of the problem, area bounded by the two paraboli is twice the area of the triangle. All these yield k=27/4(b+1) and 27(b^2)/4(b+1)=3(b+1) or b=2(since b is positive). Therefore k=27/4(2+1)=9/4.
I believe you have a typo on a^2=[k/(b+1)]+[ bk /(b+1)]^2=4k/(b+1), it should be a^2=[k/(b+1)]+[ k /(b+1)]^2=4k/(b+1)
Log in to reply
The vertex of the second parabola is at (0,k), and the point of intersection of the two paraboli in the first quadrant is at (√(k/(b+1)), k/(b+1)). Distance between these two points, which is the length of the side of the equilateral triangle is √((0-√k/(b+1))^2+(k-(k/(b+1)))^2) which is equal to what I have written.
Log in to reply
Oh, you are correct, my mistake
Log in to reply
@David Vreken – It's OK. Anyway, I like your problems. Carry on.
p1 = x 2 and p 2 = y − a x 2 . Both a and y are arbitary parameters presently and will be computed later. The values of x at the intersections are ± a + 1 y . The value of y at the intersections is a + 1 y . Equating the area of the triangle and one-half of the area between the parabolas and solving for a gives 2 . Equating the Euclidean length of a side and the base to make the triangle isosceles and solving for y gives 4 9 . Adding the numerator and the denominator gives 13.
Let the equation of the inverted parabola be y = c − k x 2 . Then c is the y -intercept we need to find. The intersecting points of the two parabolas or the bottom two vertices of the equilateral triangle ( ± x 1 , y 1 ) satisfy the system of equations of parabola.
{ y = x 2 y = c − k x 2 . . . ( 1 ) . . . ( 2 ) ⟹ x 2 = c − k x 2 ⟹ x 1 = ± k + 1 c
Let the altitude of triangle be h , then we have:
c k + 1 k c = y 1 + h = x 1 2 + 3 x 1 = k + 1 c + k + 1 3 c = k + 1 3 c
⟹ c = k 2 3 ( k + 1 ) , x 1 = k 3 , and area of the triangle A △ = k 2 3 3 .
Since A △ is same as the area between the parabolas and triangle, the area enclosed by the parabolas A p = 2 A △ or 2 1 A p = A △ . And we have:
2 1 A p = ∫ 0 x 1 ( c − k x 2 − x 2 ) d x = ∫ 0 k 3 ( k 2 3 ( k + 1 ) − ( k + 1 ) x 2 ) d x = [ k 2 3 ( k + 1 ) x − 3 k + 1 x 3 ] 0 k 3 = k 3 2 3 ( k + 1 ) Note that c = k 2 3 ( k + 1 )
Therefore, k 3 2 3 ( k + 1 ) = k 2 3 3 ⟹ 2 k + 2 = 3 k ⟹ k = 2 , c = k 2 3 ( k + 1 ) = 4 9 , and a + b = 9 + 4 = 1 3 .