Two Sided Pulley!
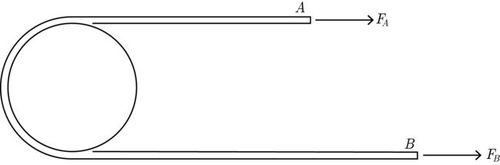There is a light, inelastic thread is stretched round one half of the circumference of a fixed cylinder as shown above.
As a result of friction, the thread does not slip on the cylinder when the magnitudes of the forces acting on the ends satisfy the inequality 2 1 F A ≤ F B ≤ 2 F A
Determine the coefficient of friction μ between the thread and the cylinder.
The answer is 0.2206356.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
It is also called Euler's relation.
P.S:- I did an experimental verification of this at OCSC.
Log in to reply
Did you plot something like a e^x graph?
Log in to reply
Yeah, first we collected data then we did graph plotting to verify the relation.
Your problems are really challenging and nice. Are these original?
Log in to reply
No. They are not original man. I heard from some one that these are from FIITJEE book.
Log in to reply
Nope these aren't from FIITJEE books... Don't just assume like this...
Log in to reply
@Kishore S. Shenoy – Okay man. No offense. Only defence :P
Log in to reply
@Surya Prakash – Hehe. No problem!
Log in to reply
@Kishore S. Shenoy – Hey. I have a doubt. Are the problems from FIITJEE book very nice , i mean like are they awesome?
Log in to reply
@Surya Prakash – Two or three in a chapter textbook.
I get good questions from different sources and post it so that it can help others too... ⌣ ¨
Log in to reply
It would be nice if you could credit the source too. You seem to have an incredible knowledge in mechanics.
Log in to reply
@Jayakumar Krishnan – Me? Don't think so! What we know is just a drop!
@Jayakumar Krishnan – Done! Thank you!
@Jayakumar Krishnan – Try All that matters is the constant velocity!
Now, F A = F 0 , F B = F ( π ) = F 0 e μ π
If 2 1 F A ≤ F B , then, μ ≤ 0 [ Not possible ]
Else F b ≤ 2 F A ⇒ μ ≤ π 1 ln 2
We need maximum μ because friction always balances d F
∴ μ = π 1 ln 2
CreDit : 200 Puzzling Physics Problems