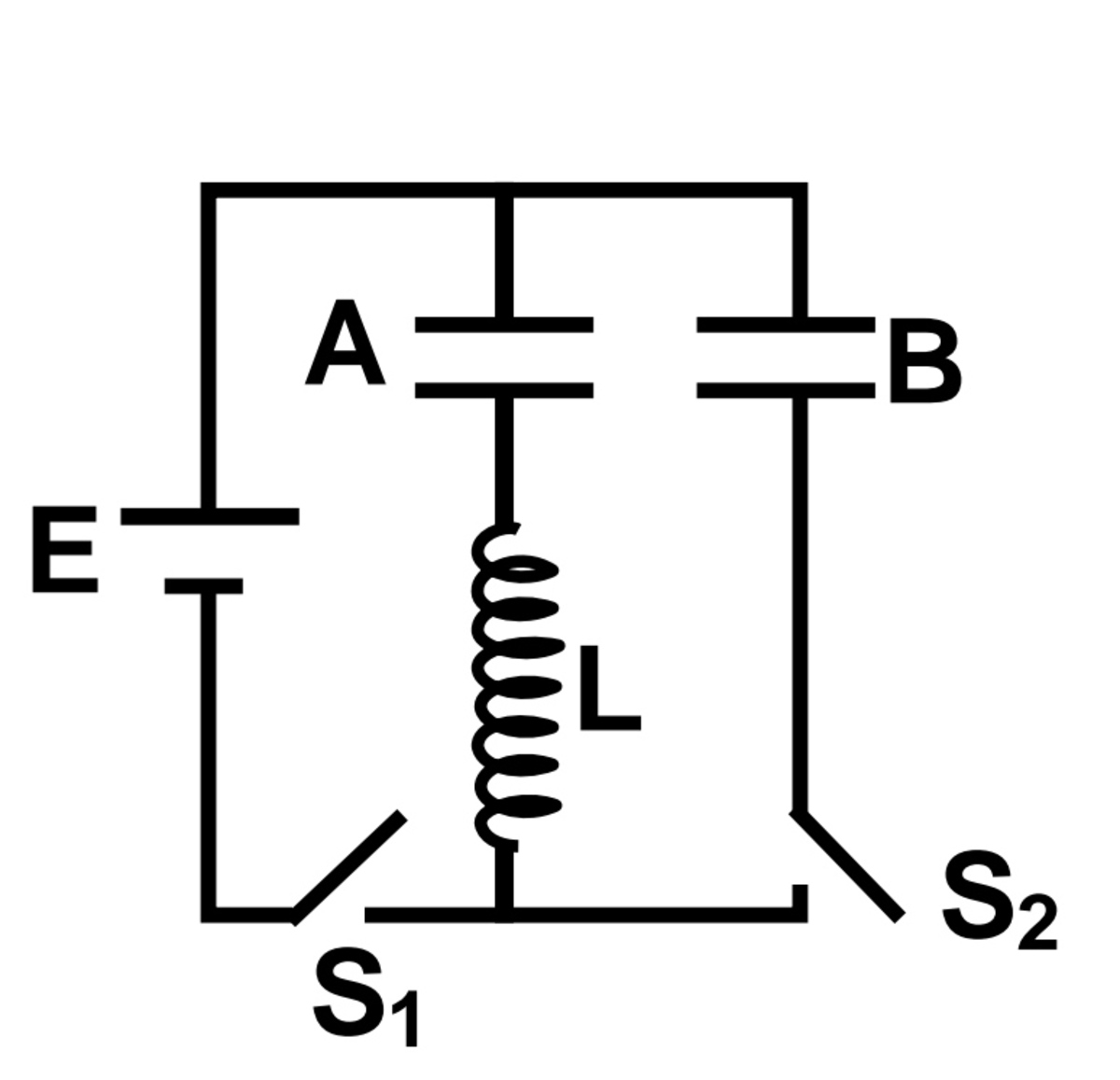
Two Uncharged Capacitors
Two uncharged identical capacitors
A
and
B
, each of capacitance
C
and an
inductor of inductance
L
are arranged as shown in the adjacent figure. At
t
=
0
the
S
1
is closed while switch
S
2
remains open. At time
t
=
t
0
=
L
C
2
π
, switch
S
2
is closed while switch
s
1
is opened.
The charge on capacitor
A
after time
t
0
is
α
C
E
The current flowing through the inductor at
t
=
t
0
is
β
L
C
C
E
After switch
S
2
is closed and
S
1
is opened, the maximum value of current through the inductor is
(
δ
L
γ
C
)
E
Type your answer as
α
+
β
+
γ
+
δ
=
?
Details and Assumptions
1)
α
,
β
,
γ
,
δ
all four are integers.
2)
γ
,
δ
are co-prime numbers.
3)
The wire used in the circuit have 0 resistance.
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Guilherme Niedu Sir Thanks for your solution through Laplace transformation, it will help me to understand how to solve this questions through Laplace.
Several intermediate calculation and simplification steps in the solution below are left out.
When S 1 is closed, capacitor B is disconnected and the circuit equation reads:
− E + C Q A + L I ˙ = 0 I = Q ˙ A
Q A ( 0 ) = 0 I ( 0 ) = 0
⟹ Q ¨ A + L C Q A = L E
The solution to the above equation after considering initial conditions comes out to be:
Q A = C E ( 1 − cos ( L C t ) ) I = Q ˙ A = L C C E cos ( L C t )
It follows immediately that at t = 2 π L C :
Q A = C E I = L C C E
⟹ α = 1 ; β = 1
At this instant, the switch S 1 is opened and S 2 is closed. For this scenario let the charge on capacitor A be Q A and that on capacitor B be Q B . Treating this instant as time t = 0 , the convention used here is that at a general time t the current through the inductor flows upwards (as viewed in the given diagram) and capacitor A is discharging while B is charging. Keeping in mind, the circuit equation reads:
L I ˙ = C Q A − C Q B … ( 1 ) I = − Q ˙ A = Q ˙ B Q A ( 0 ) = C E Q B ( 0 ) = 0 I ( 0 ) = − L C C E
From (1): I ˙ ( 0 ) = L E
Re-arranging to obtain and ODE governing the evolution of I leads to:
I ¨ + ( L C 2 ) I = 0
Let:
ω 2 = L C 2
Solving the above equation and applying initial conditions gives:
I = 2 L C C E sin ( ω t ) − L C C E cos ( ω t )
Using a bit of trigonometry, the current amplitude can be computed. The value is:
I m a x = 2 L 3 C E
⟹ γ = 3 ; δ = 2
The required answer is: 7 .
@Karan Chatrath Yeah ,very good solution.
@Karan Chatrath which tool you use for making the circuits showing inductor, resistor etc. Can i make them In mobile?
Log in to reply
I posted a report for your recent problem. I stand corrected. I think that the answer to that problem is not an integer. Please re-check.
As for diagrams, I use diagrams.net. It is freely available on the internet.
Log in to reply
@Karan Chatrath Sir there is no need of charge, and the answer is an integer.
Log in to reply
@A Former Brilliant Member – Yes, you are right that charge is not needed. But I think that the answer is not an integer. I have done it analytically and using code as well, so please check once more.
@A Former Brilliant Member – I stand corrected. I made a mistake in my work on that problem. I will delete my report soon. It was a nice problem.
@Karan Chatrath
I am planning to post a good mechanics problem, but not able to solve . Will you help me?
Thanks in advance
Please reply.
Log in to reply
Sure, I will try
Log in to reply
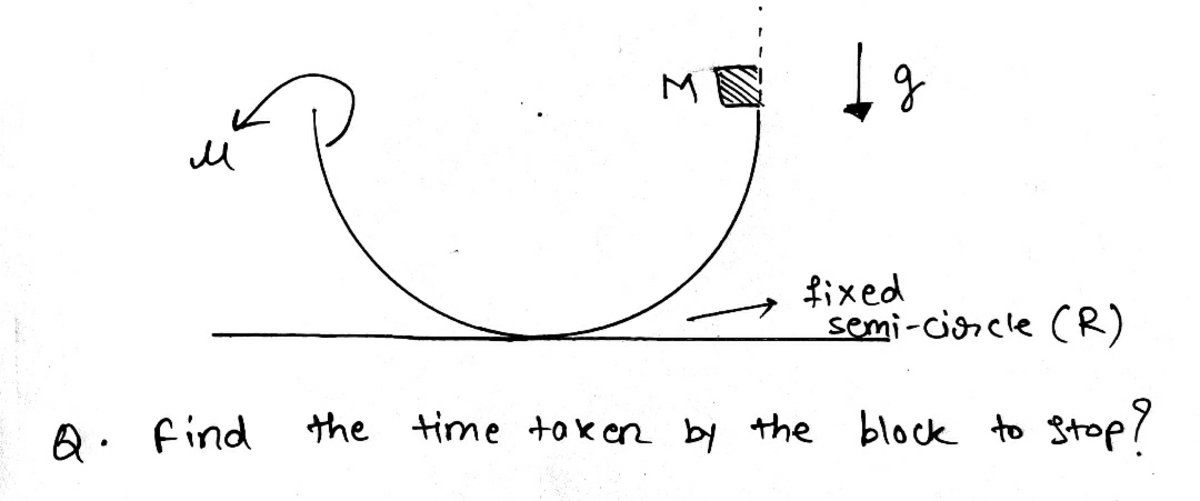
@Karan Chatrath
sir
Consider
M
=
1
g
=
1
0
R
=
1
μ
=
0
.
5
Log in to reply
@A Former Brilliant Member – Is the mass released initially from rest? Also, what difficulty did you face while solving?
Log in to reply
@Karan Chatrath – @Karan Chatrath sir yes it is freely released.
After writing equations I reached here
1
0
sin
θ
−
2
N
=
θ
¨
N
−
1
0
cos
θ
=
θ
˙
2
One energy equation we can also write but we have to include work done by friction also which is I think bit difficut task .
Now from here guide me
Thanks in advance
Log in to reply
@A Former Brilliant Member – I think you chose θ as the angle to the vertical? Anyway, so eliminate N from the equations and you will get:
θ ¨ + 2 θ ˙ 2 = 5 ( 2 sin θ − cos θ )
Use the fact that:
θ ¨ = θ ˙ d θ d θ ˙
⟹ θ ˙ d θ d θ ˙ + 2 θ ˙ 2 = 5 ( 2 sin θ − cos θ )
Multiplying both sides by e θ :
⟹ d θ d ( e θ 2 θ ˙ 2 ) = 5 e θ ( 2 sin θ − cos θ ) ]
Integrate both sides and apply initial conditions. Finally, you should get: 2 θ ˙ 2 = f ( θ )
Where f ( θ ) is some function. Notice that the LHS is the kinetic energy of the mass. The mass has initially zero KE. Plot this function and see at what time ( t > 0 ) the KE of the mass becomes zero, or solve it if you can.
I have not solved it myself so I don't know the answer. But this is how I would do it.
Log in to reply
@Karan Chatrath
–
@Karan Chatrath sir i am getting this
2
e
θ
θ
˙
2
=
2
−
5
e
θ
(
3
cos
θ
−
sin
θ
)
−
2
5
e
2
π
Log in to reply
@A Former Brilliant Member – Okay. So from here, you can get the form:
2 θ ˙ 2 = f ( θ )
Right?
Log in to reply
@Karan Chatrath
–
@Karan Chatrath
sir aapne bhi usko solve kiya hai kya??
Sir kyoki mai jab aage solve kar rha tha to mujhe
θ
=
2
π
pe block rukh rha tha
Jo thoda mujhe galat laga
@Karan Chatrath
sir what happened?
Why you stopped replying?
I have added my work at very below.
Thanks in advance.
@Karan Chatrath
I was making a problem but not able to solve?
Will you help me now?
Thanks in advance
Please reply
@Karan Chatrath
Sir I want to learn laplace transformation, but i am able to, guide me.
Consider me as your student and please guide from where should I study.
Thanks in advance.
Log in to reply
Follow this link
https://tutorial.math.lamar.edu/Classes/DE/LaplaceIntro.aspx
Log in to reply
@Karan Chatrath
Sir samajh nhi aarha
Bahut koshish kar rha.
Kya karu aapke hisab se par mujhe padhna hihai??
Log in to reply
@A Former Brilliant Member – According to me, it is useful knowledge. But whether you want to learn is up to you. I think it is quite well explained there. The laplace transform is simply an integral. Consider a function f ( t ) . Then its laplace transform is:
L ( f ( t ) ) = ∫ 0 ∞ e − s t f ( t ) d t
The above is the main definition. So use this definition and try to compute the Laplace transform of f ( t ) = sin t , f ( t ) = cos t , f ( t ) = e t and f ( t ) = t n . See what result you get for each function, and check your results by searching on the internet. The link I gave you is actually helpful. Skip to the part where the definition of the Laplace transform is given.
Log in to reply
@Karan Chatrath – @Karan Chatrath is s constant???
Log in to reply
@A Former Brilliant Member – Yes, treat the s as a constant while integrating.
Log in to reply
@Karan Chatrath
–
@Karan Chatrath Sir I am getting this
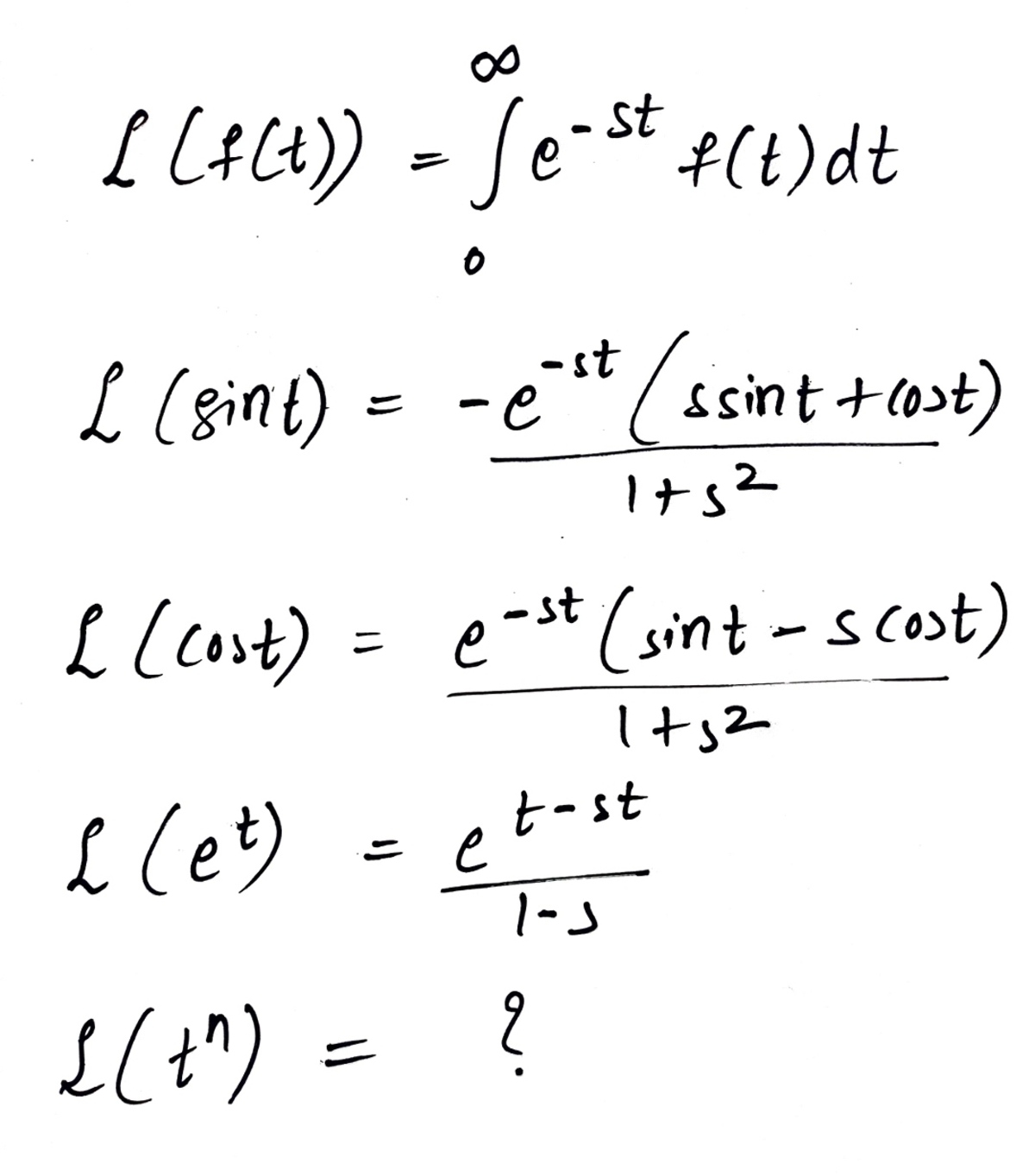
And not able to solve that last one
t
n
When I am using online calculator, I am not getting that which I solved
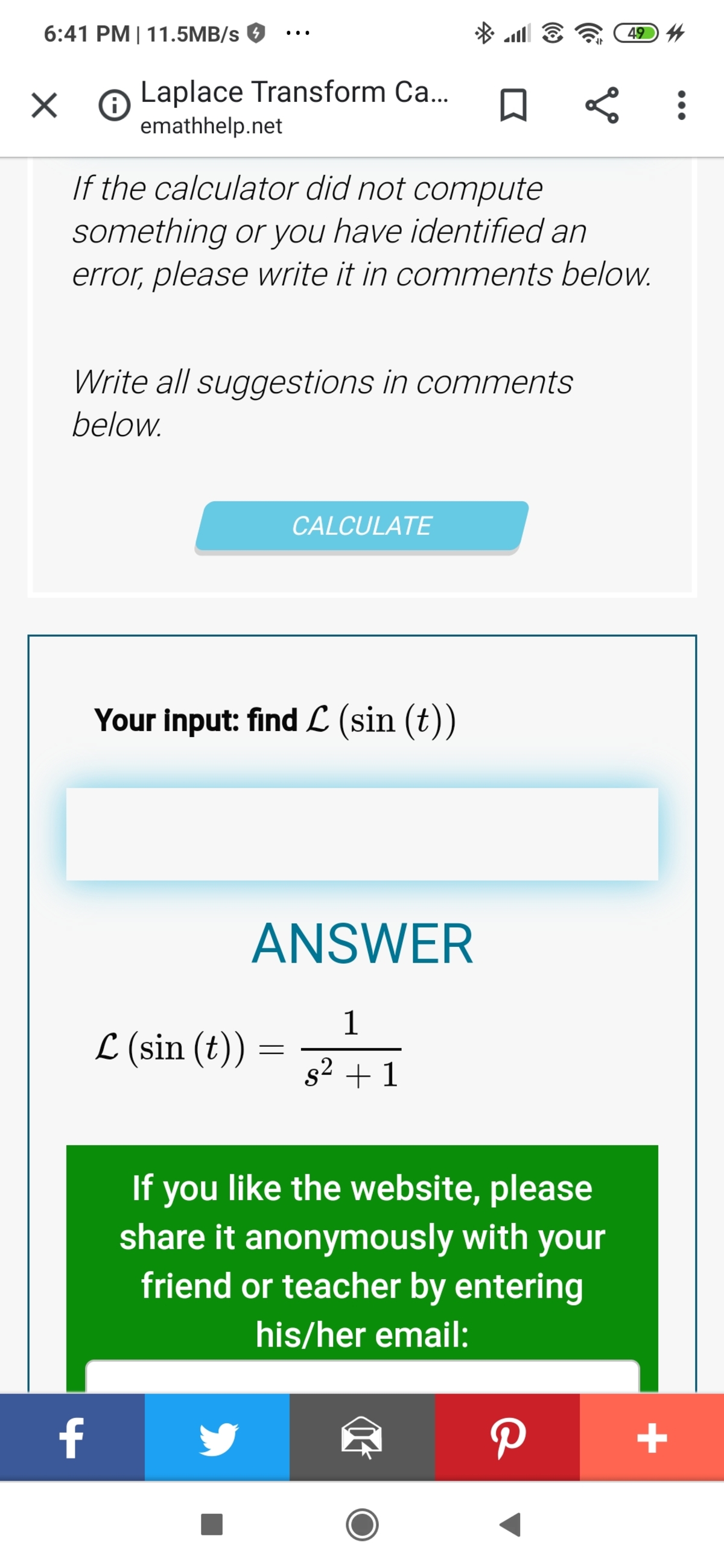
Thanks in advance.
Log in to reply
@A Former Brilliant Member – You have a definite integral with respect to t and your results are in terms of t . That is obviously wrong. Apply the limits of integration.
Log in to reply
@Karan Chatrath
–
@Karan Chatrath
Oh sorry
Yes now I am getting everything correct!
But how to apply this in electricity problems.
Log in to reply
@A Former Brilliant Member – Read about solving differential equations using Laplace transform technique.
@Karan Chatrath
here below what will be the charge as a function of time and heat dissipated bin the resistors
I have little bit forget the concept.
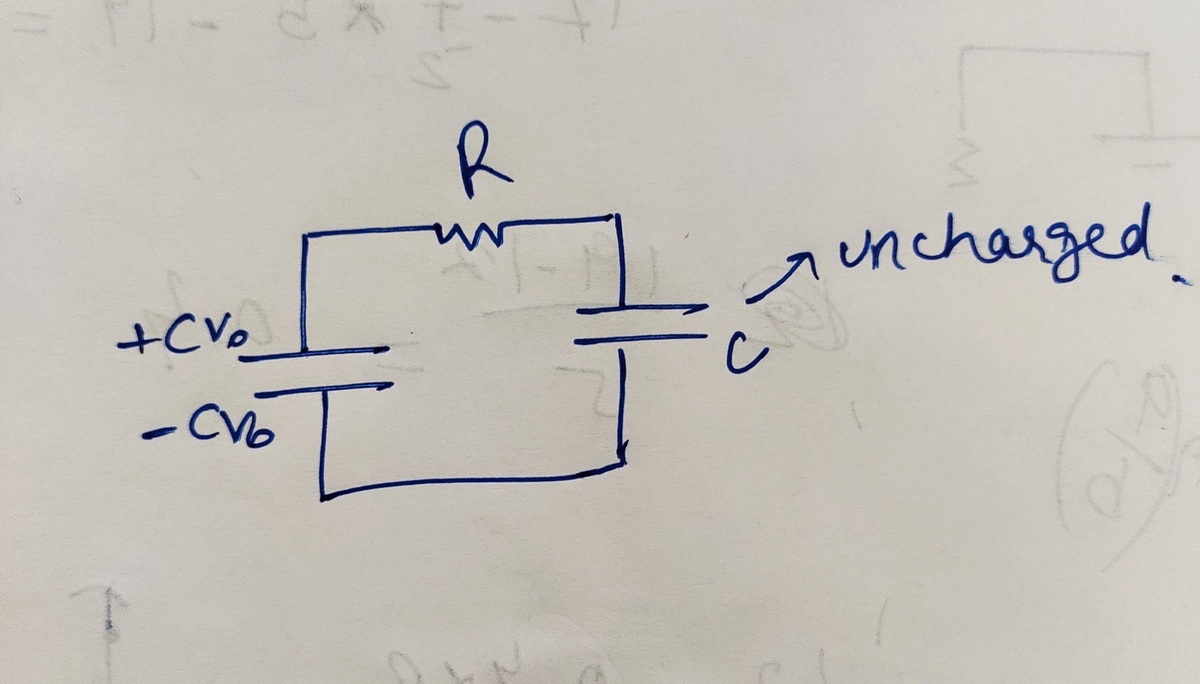
Log in to reply
Apply Kirchoff's law and solve the resulting differential equation. If you want you can show what result you get.
Between t = 0 and t = t 0 :
E = C 1 ∫ 0 t i ( τ ) d τ + L d t d i
Apllying Laplace transform :
s E = C s 1 I ( s ) + L s I ( s )
I ( s ) = L C s 2 + 1 E C
I ( s ) = L C C E ⋅ s 2 + L C 1 L C 1
So:
i ( t ) = L C C E sin ( L C 1 t )
Likewise the voltage on capacitor A is:
V A ( s ) = C s 1 I ( s ) = s ( L C s 2 + 1 ) E
V A ( s ) = s E − s 2 + L C 1 E s
v A ( t ) = E [ 1 − cos ( L C 1 t ) ]
So:
i ( t 0 ) = L C C E → β = 1
v A ( t 0 ) = E → q A ( t 0 ) = C E → α = 1
After t 0 :
On capacitor A :
( i ) i ( t ) = C d t d v A ( t ) , v A ( t 0 ) = E
On capacitor B :
( i i ) i ( t ) = C d t d v B ( t ) , v B ( t 0 ) = 0
On inductor:
( i i i ) L d t d i ( t ) = v L ( t ) , i ( t 0 ) = L C C E
Applying laplace again on three equations:
( i ) I ( s ) = C ( s V A ( s ) − E )
( i i ) I ( s ) = C s V B ( s )
( i i i ) L ( s I ( s ) − L C C E ) = V L ( s )
Multuplying ( i i i ) by C s and rearranging:
( i ) I ( s ) = C s V A ( s ) − C E
( i i ) I ( s ) = C s V B ( s )
( i i i ) L C s 2 I ( s ) = C s V L ( s ) + C E L C s
Adding up the three equations and remembering that V A + V B + V L = 0 , since we have a closed loop:
( L C s 2 + 2 ) I ( s ) = C E L C s − C E
I ( s ) = C E ( L C s 2 + 2 L C s − L C s 2 + 2 1 )
I ( s ) = C E ⎝ ⎜ ⎜ ⎛ L C 1 ⋅ s 2 + L C 2 s − 2 L C 1 ⋅ s 2 + L C 2 L C 2 ⎠ ⎟ ⎟ ⎞
I ( s ) = 2 L C C E ⎝ ⎜ ⎜ ⎛ 2 ⋅ s 2 + L C 2 s − s 2 + L C 2 L C 2 ⎠ ⎟ ⎟ ⎞
So:
i ( t ) = 2 L C C E ⎣ ⎡ 2 cos ⎝ ⎛ L C 2 t ⎠ ⎞ − sin ⎝ ⎛ L C 2 t ⎠ ⎞ ⎦ ⎤
Multiplying above and below by 3 :
i ( t ) = E 2 L 3 C ⎣ ⎡ 3 2 cos ⎝ ⎛ L C 2 t ⎠ ⎞ − 3 1 sin ⎝ ⎛ L C 2 t ⎠ ⎞ ⎦ ⎤
Let ω = L C 2 and ϕ such that cos ( ϕ ) = 3 2 , we will also have sin ( ϕ ) = 3 1 . So:
i ( t ) = E 2 L 3 C [ cos ( ϕ ) cos ( ω t ) − sin ( ϕ ) sin ( ω t ) ]
i ( t ) = E 2 L 3 C cos ( ω t + ϕ )
So:
I m a x = E 2 L 3 C → γ = 3 , δ = 2
Thus:
α + β + γ + δ = 7