U tubes are tricky!

Classical Mechanics Level 5

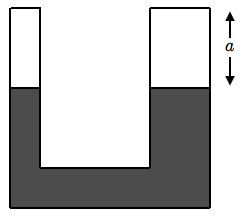A U-tube is filled with mercury as shown below, leaving a distance $a$ without filling. The cross section of the right hand of the tube is twice the cross section of the left one. Water is then poured water on the right hand of the tube until the water level reaches the top of the right side. If the level of mercury in the left side of the tube rises a distance

$H=\frac{b}{c}a$

where $b$ and $c$ are positive co-prime integers, find the value of $b+c$ .

Take the density of mercury to be 13.6 times the density of water.

This problem is not original. It is taken from this year's Second Round of the Colombian Physics Olympiad.

The answer is 209.

1 solution

Sriram Vudayagiri
Sep 19, 2015

The cross section of left tube is half that of right tube. So, if mercury rises by x on left tube, mercury level falls by $\frac {x}{2}$ on the other.

So, the total height of water column is a + $\frac {x}{2}$

Now, at equilibrium, pressure at point A should be equal to pressure at point B.

$P_{A}$ = $P_{0}$ + (a + $\frac {x}{2}$ ) * 1 * g + (L - $\frac {x}{2}$ ) * 13.6 * g

$P_{B}$ = $P_{0}$ + (x + L) * 13.6 * g

Equating $P_{A}$ and $P_{B}$ and solving,

we get x = $(\frac {10}{199})$ a.

Nicely done Sriram! Just a few corrections:

Based on your solution, your $L$ should go all the way up to the dotted lines in your sketch.

Also, you forgot to use $g$ on your solution. I know that at the end it ends up going away from both side of the equation but they need to be on the expressions for $P_A$ and $P_B$ .

Miguel Vásquez Vega - 5 years, 8 months ago

Hi and thanks for that. I've added g but whats wrong with the diagram bro? Whats wrong with L?

Sriram Vudayagiri - 5 years, 8 months ago

You're right, it seemed to me before that it didn't. Haha forget about that. That's the solution! ;)

Miguel Vásquez Vega - 5 years, 8 months ago

@Miguel Vásquez Vega – Thanks.. @Miguel Vásquez Vega

Sriram Vudayagiri - 5 years, 8 months ago

@Sriram Vudayagiri – Shouldn't 'L' be till the end of the tube?i mean shouldn't it be till the base i.e the least point of the tube?

Harisam Sharma - 5 years, 5 months ago

L stretches till the dotted lines...

Sriram Vudayagiri - 5 years, 8 months ago

U tubes are tricky!

This problem is not original. It is taken from this year's Second Round of the Colombian Physics Olympiad.

The answer is 209.

1 solution

0 pending reports