Aurora Borealis

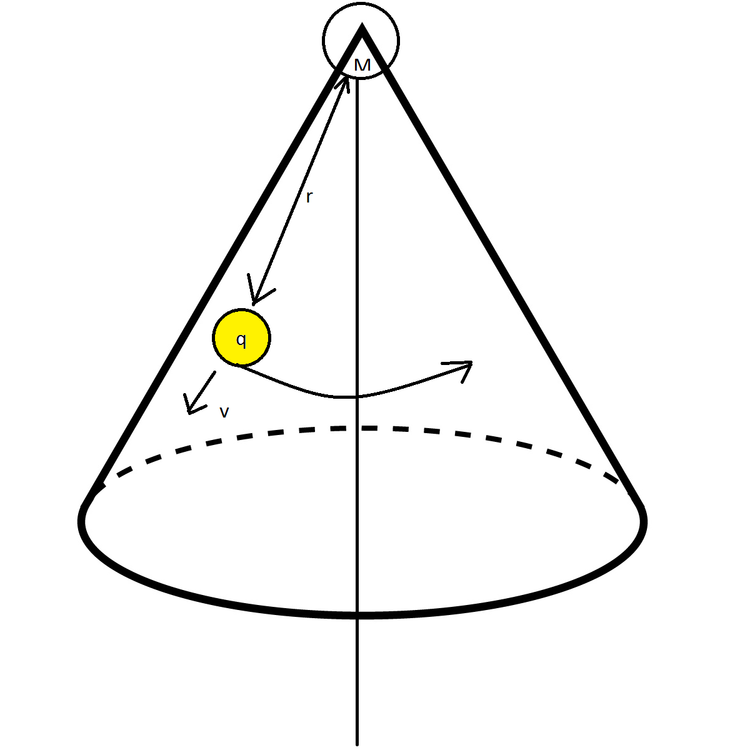Imagine a magnetic charge as shown in the figure of strength $m$ , its magnetic field vector can be expressed as $\dfrac {kr}{|r|^{2}}$ where $r$ is the radial position vector of any point from the magnetic charge.

An electric charge has been released in its vicinity at a distance of $r_{o}$ with a radial velocity component $v_{o}$ and some arbitary angular velocity $w_{o}$ about the cone's axis and it now moves in the magnetic field of the magnetic charge.

It moves on the surface of a cone of half angle $\alpha$ with its vertex at the magnetic charge (Refer to figure above).

If its radial speed $v$ at any time can be related to other quantities as

$\displaystyle {(f) v_{o}}^{(e)} - \frac { L^{g}}{(a) m^{(c)} \sin^{(b)}(\alpha )} \left [ \frac {1}{{r_{o}}^{(d)}} - \frac {1}{r^{(d)}} \right ] = {(f) v^{(e)}}$

For positive integers $a,b,c,d,e,f,g$ , evaluate $\frac {1}{2} abcdefg$

Details and Assumptions

$L$ is the Initial angular momentum about cones axis

$m$ is the mass of electrical charge

$r$ is the radial distance

$v$ is the radial velocity magnitude

$v_{o}$ is the Initial radial velocity

you may want to try this problem first

$Details$

• A magnetic charge is simply a magnetic analogue of electrical charge, it produces a radial magnetic field and though its existence is uncertain. Assume it exists for this problem.

• The force upon an electric charge in a magnetic field is given by $q(v \times B)$

• The explicit independence of $k$ from the relation is not an error.

• (Fun Fact) The beautiful northern lights or Aurora Borealis is the result of this phenomenon where charged particles funnel in like a cone into the north pole and keep moving in the surface of the cone, Though yes ours is a highly idealised and simplfied situation.