UMCYM #30

A trivial solution to the system of equations is $(0,0,0)$ . For $x, y, z \ne 0$ , we can consider taking reciprocal of the three equations and adding them together.

$\begin{cases} \dfrac 1{4x^2} + 1 = \dfrac 1y \\ \dfrac 1{4y^2} + 1 = \dfrac 1z \\ \dfrac 1{4z^2} + 1 = \dfrac 1x \end{cases}$

$\begin{aligned} \frac 1{4x^2} - \frac 1x + 1 + \frac 1{4y^2} - \frac 1y + 1 + \frac 1{4z^2} - \frac 1z + 1 & = 0 \\ \left(\frac 1{2x} - 1 \right)^2 + \left(\frac 1{2y} - 1 \right)^2 + \left(\frac 1{2z} - 1 \right)^2 & = 0 \end{aligned}$

Note that $\left(\dfrac 1{2x} - 1 \right)^2 \ge 0$ , $\left(\dfrac 1{2y} - 1 \right)^2 \ge 0$ and $\left(\dfrac 1{2z} - 1 \right)^2 \ge 0$ . All three square factors have to be equal to 0 simultaneously to be equal to the RHS. Therefore, there is only one more solution, $\left(\frac 12, \frac 12, \frac 12 \right)$ , altogether $\boxed{2}$ triplet solutions.

Let $f(x) = \frac{ 4x^2 } { 1 + 4x^2 }$ .

The system of equations tells us that $f(x) = y, f(y) = z, f(z) = x$ . Thus, we are looking for fixed points which satisfy $f(f(f(x))) = x$ .

Observation 1: Calculating the solutions of $f(f(f(x))) = x$ would lead to solving a really ugly polynomial, so let's try a different approach.

Observation 2: We would love to claim that $f(f(f(x))) = x \Rightarrow f(x) = x$ . While we know that this is a sufficient condition, we do not know if it is necessary.

Observation 3: All of the variables are non-negative.

Let's consider the graphs of $y = f(x)$ and $y = x$ when $x \geq 0$ .

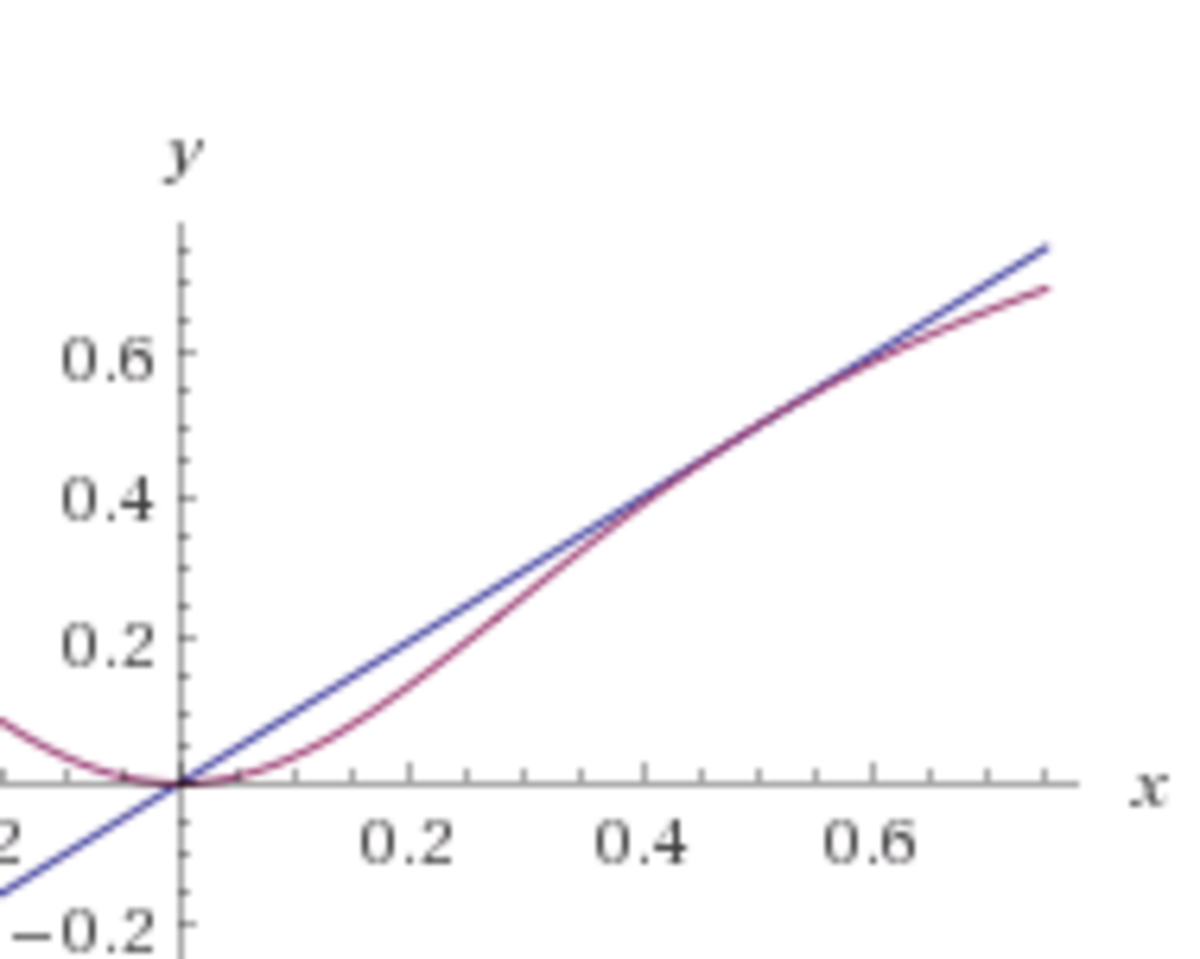
We see that when $f(x) \leq x$ . Furthermore, if $x \neq 0, \frac{1}{2}$ , then we have $f(x) < x$ . Applying this to the problem, if $x \neq 0, \frac{1}{2}$ , then we can conclude that

$f(f(f(x))) \leq f(f(x)) \leq f(x) < x$

which tells us that there are no solutions to $f(f(f(x))) = x$ !

Hence the only solution comes when $x = 0$ or $\frac{1}{2}$ . Which these values, we can uniquely determine $y$ and $z$ accordingly.

---

Note: The other solutions to the really ugly polynomial $f(f(f(x))) = x$ are complex valued.

The only solutions are (0,0,0) and (0.5,0.5,0.5). Hopefully someone will post a good solution? My solution isn't great complete enough.