Unbalanced Maximum
Given that x , y are real numbers that satisfy the equation x 2 + y 2 = 1 4 x + 6 y + 6 , what is the maximum value of 3 x + 4 y ?
The answer is 73.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
19 solutions
Why is the maximum of 3 3 + 2 4 cos θ + 3 2 sin θ 2 4 2 + 3 2 2 ?
Log in to reply
Because a sin x + b cos x = a 2 + b 2 ( a 2 + b 2 a sin x + a 2 + b 2 b cos x ) = a 2 + b 2 ( cos y sin x + sin y cos x ) = a 2 + b 2 sin ( x + y ) ≥ a 2 + b 2
where y = arccos a 2 + b 2 a .
Log in to reply
The inequality sign should be ≤ instead of ≥ .
You can either use the method suggested by 'Jan' to prove this result or you can do the following:
Take
ψ
=
2
4
cos
θ
+
3
2
sin
θ
⇒ d θ d ψ = − 2 4 sin θ + 3 2 cos θ
For ψ to be maximum, d θ d ψ = 0
⇒ 2 4 sin θ = 3 2 cos θ
⇒ tan θ = 3 4
Hence, we find,
sin θ = 5 4 a n d cos θ = 5 3
Substituting these values in
ψ
,
we find,
ψ m = 4 0 , where ψ m denotes the maximum possible value of ψ
To confirm,
2 4 2 + 3 2 2 also evaluates to 4 0 .
Because using R-formula, you get 3 2 sin θ + 2 4 cos θ = 2 4 2 + 3 2 2 sin ( θ + tan − 1 3 2 2 4 ) . Since the maximum of any sin function is 1 , the maximum of 3 2 sin θ + 2 4 cos θ = 2 4 2 + 3 2 2 when sin ( θ + tan − 1 3 2 2 4 ) = 1 .
or you can calculate the derivative, equate it with 0, and you get 32 cos theta - 24 sin theta = 0, factor 8 cos theta and you get that tan theta is 4/3 which will give cos theta = 3/5 and sin theta= 4/5 and then you get x=11.8 and y=9.4
Awesome solution! :D
Nice solution! :D Didn't think of this!
Nice one dude. this is waaaay more simpler than mine, (actually I used derivative application to find the maximum value). Good Job!
Log in to reply
Thanks. Happy New Year!
cud u share ur approach plz?
Log in to reply
For more clarity, i'll share my approach. we know that
( x − 7 ) 2 + ( y − 3 ) 2 = 6 4
rearranging the equation, we get y = − x 2 + 1 4 x + 1 5 + 3
Let F = 3 x + 4 y substituting the y value to F yields
F = 3 x + 4 ( − x 2 + 1 4 x + 1 5 ) + 1 2
using the derivative application, in order to get x that maximizes F , d ( F ) / d x has to be 0. then after we derivate F, we get
F ′ = 3 − x 2 + 1 4 x + 1 5 − 4 x + 2 8 = 0
solving F ′ for x , we get x = 5 9 / 5 or x = 1 1 / 5
with those x values we could get the corresponding y value, then look which one yields the bigger value of F . at last, the maximum will occur when x = 5 9 / 5 and y = 4 7 / 5 which is 7 3
I have already posted a comment on the derivative approach. Just scroll up.
is this substitution a standard technique? In what chapter do we learn it Conic sections?
Log in to reply
The given equation is obviously a Circle, so what I have substituted is the parametric coordinates of a general point that lies on that circle. So you will find this in the Circles Chapter of any standard Math book, and search for parametric coordinates.
Log in to reply
Alright! Thanks! Haven't noticed that!
thank you!
@Anish Puthuraya - Can you please please suggest me a resource or explain the topic of parametric co-ordinates and their application using polar cooridnates to solve inequalities like above? I would really appreciate it. Thanks
Log in to reply
@Jayakumar Krishnan – Really, any standard maths book would do...But, if you would like a more specific resource, then check out S.L.Loney Coordinate Geometry.
Log in to reply
@Anish Puthuraya – Sorry but I couldn't find anything related in tht book. Could you help me out?
@Anish Puthuraya – @Anish Puthuraya
can you tell me what is the problem if I differentiate this equation wrt x first time to get a maximum for x and another time to get a maximum of y which does give me x=7 and y<3 but the thing inside the root?..thanks again
Log in to reply
Assuming that you have partially differentiated wrt x and then again with y , I would like to share a general property of conics ( in this case, a circle)....
When you partially differentiate a circle wrt x , you get an equation which represents one of the diameters of the circle. And similarly, with y , you get one more equation which is also a diameter.
Thus, if you solve these 2 equations, the solutions will give you the center of the circle and not the maximum value of either x or y .
And even if you somehow did find the maximum value of x and y , that will not ensure that 3 x + 4 y will be maximised.
thanks
Brilliant solution! Can you share your motivation, please?
How do you surely know that the expression will be maximum at x = 7 + 8 cos θ and y = 3 + 8 sin θ , and not any other value instead of this one?
Log in to reply
You are mistaken. I didn't do that substitution so that I'll get a maximum. This is what is called a Parametric Substitution. Just plug-in x = 7 + 8 cos θ and y = 3 + 8 sin θ in the original given equation. You will find that it simplifies to sin 2 θ + cos 2 θ = 1 , which is always true.
This implies that I can now use this substitution anywhere I want. In this case, I substituted x = 7 + 8 cos θ and y = 3 + 8 sin θ in 3 x + 4 y to get 3 3 + 2 4 cos θ + 3 2 sin θ .
Then, I maximized this expression instead. I hope I didn't confuse you too much.
Great solution!
as elegant as it can get
I approached it like :
We have a circle having center at (7,3) and radius =8.
Now check where a line 3x+4y=k intersects , and find corresponding maximum for k.
But yours looks easy on calculation. :)
Log in to reply
But, that line might intersect the circle at 2 points. So, you would have to make that line tangential to the circle , and then find the value of k, which would be automatically maximum.
Log in to reply
Exactly. But your solution is smart. Quick and easy .
Just a thought, couldn't we look at the maximum value of 3x + 4y as related to the furthest point on the x-axis which intersects the circle and which we can look at as the intercept of the line 4y = -3x + c ? So, the maximum value of c will be the maximum value of 3x + 4y
I did it almost like you Anish. I tried to calculate the critic points of that function and found tan theta=4/3 and got sin theta and cos theta and then x and y. It was a beautiful problem.
We see square and linear terms, let's try to form perfect squares with them:
( x 2 − 1 4 x + 4 9 ) + ( y 2 − 6 y + 9 ) = 6 + 4 9 + 9 = 6 4
( x − 7 ) 2 + ( y − 3 ) 2 = 6 4
Here we have a sum of squares, which seems suitable for Cauchy's inequality!
Since we are maximizing 3 x + 4 y , our multiplier would be ( 3 2 + 4 2 ) :
6 4 ( 3 2 + 4 2 ) = [ ( x − 7 ) 2 + ( y − 3 ) 2 ] ( 3 2 + 4 2 ) ≥ [ 3 ( x − 7 ) + 4 ( y − 3 ) ] 2 = ( 3 x + 4 y − 3 3 ) 2
4 0 2 ≥ ( 3 x + 4 y − 3 3 ) 2
4 0 ≥ 3 x + 4 y − 3 3 (we exclude the other case because that doesn't give us the maximum)
3 x + 4 y ≤ 4 0 + 3 3 = 7 3 where equality holds when y = 1 0 , x = 1 1
Cauchy isn't necessary in this problem, but cool application of you to use it. I used a more geometric / coordinates approach.
BTW, I don't believe your equality case is correct. Cauchy Schwarz has equality when the terms are linearly dependent, so we would have 3 x − 7 = 4 y − 3 . My answer which I got as ( 5 5 9 , 5 4 7 ) fits this.
Log in to reply
A very nice problem! It seems that there are many completely different solutions.
Can you post your solution here? I would be interested to see a solution using geometry. (Mainly because this problem seems like an algebra problem)
Log in to reply
quick outline of my solution, which was geometric: basically you want to maximize 3x+4y=k, which is a line with slope -3/4. since maximizing the intercepts is equivalent to maximizing k, we choose the line with the greatest intercepts. this is the line that's tangent to the circle. from here there are many ways to find said line.
Log in to reply
@Henrik Boecken – This is what I used. Maximize that k, so it's the line tangent to the circle, meaning that the radius has a sloep of 3 4 , and we know the radius of the circle and the center so we can find the point of tangency ( x , y ) and then substitute it into our equation 3 x + 4 y .
@Henrik Boecken – mine was a pretty much the same approach 'coz I also wanted to use a geometric one...:)
I agree with Michael Tong. y = 10, x = 11 is not a solution. The maximum value of 73 occurs at y = 47/5 and x = 59/5.
Nice spproach looks correct to me
What is Cauchy's inequality
Log in to reply
Its a standard inequality stating that,
If u and v represent two non-zero vectors, then,
∣ u . v ∣ ≤ ∣ u ∣ ⋅ ∣ v ∣
Now, let
u
=
x
1
i
^
+
x
2
j
^
v
=
y
1
i
^
+
y
2
j
^
N o t e : Here, we have considered 2-dimensional system, but this inequality will hold for n-dimensional system as well.
Thus, the inequality clearly simplifies to,
x 1 ⋅ y 1 + x 2 ⋅ y 2 ≤ x 1 2 + x 2 2 ⋅ y 1 2 + y 2 2
Here, in this problem, we let,
u
=
3
i
^
+
4
j
^
v
=
(
x
−
7
)
i
^
+
(
y
−
3
)
j
^
Then substituting these values of u and v , and squaring. we get the inequality suggested by Xuming (very well done, Brother)
Log in to reply
u r not 16 yr old .... r u?
From the condition we get y = − x 2 + 4 x + 1 5 + 3 (we ignore the second root, because 3 x + 4 y is increasing in y and this root is clearly the larger one). Thus we wish to maximize f ( x ) = 3 x + 4 ( − x 2 + 4 x + 1 5 + 3 ) Note that f ′ ( x ) = − x 2 + 1 4 x + 1 5 3 − x 2 + 1 4 x + 1 5 − 4 x + 2 8 = 0 i.e. 3 − x 2 + 1 4 x + 1 5 = 4 x − 2 8 Squaring both sides yields ( 5 x − 1 1 ) ( 5 x − 5 9 ) = 0 The solution 5 1 1 is extraneous, hence f ( 5 5 9 ) = 7 3 is the maximum, which can be also verified by checking convexity/concavity of f ( x ) .
I was suspicious of the problem when I guessed the correct answer on my first try. This is a copy of 1996 AHSME Problem 25 .
Log in to reply
Huh, didn't know that. My friend shared me this one:P
The calculation becomes a whole lot less tedious, once you substitute u = x − 7 , v = y − 3 for x and y , respectively. Why do this? Because of the standard expression for the circle that can be obtained from completing the squares.
1) x 2 + y 2 = 1 4 x + 6 y + 6 could be writen as : ( x − 7 ) 2 + ( y − 3 ) 2 = 6 4 , this is a cercle with radi 8 centered at ( 7 ; 3 ) .
2) Let 3 x + 4 y = b , we search to maximise the parameter b , so let's use this equation in the following form : y = − 4 3 x + 4 b , this represents a line in the ( x ; y ) coordinates.
3) Find where the circle and the line intersect in one point (when the line is tangent to the cercle, two solutions here)
4) We get two values for b : b = − 7 and b = 7 3 .
Therefore the answer is 7 3 .
P.S. we could always resort to "Lagrange multipliers" to solve these kind of problems.
Nice solution! I did it similarly. I played around with using Lagrange multipliers for this and interestingly eliminating the scalar constant gave me the equation of a line that coincides with the point of interest. However, it's the line perpendicular to the one we are trying to maximize!!
Here is a video by a dude giving his own take on the problem!
Yeah Lagrange multiplier is the standard trick as always. Suppose that we have to find k for 3 x + 4 y = k so that it intersect with ( x − 7 ) + ( y − 3 ) 2 = 6 4 at exactly one point, we put y = 4 k − 4 3 x into the circle equation, find the discriminant and set it to zero. We will find two solution and of course we will pick the largest one. It's pretty clumsy but a promised way to find it.
Lagrange multipliers come in handy when number of variables involved are large and the number of conditions imposed are too many (and are inequalities). In this case, since there are only 2 variables and conditions are equality conditions, it is better to approach this using geometry or simple square completion.
I think it will be easier if you consider that line 3 x + 4 y is perpendicular with radius of circle. You can easily find that the tangent of the radius that passes through the intersection point is 3 4 by using m 1 ⋅ m 2 = − 1 . Then just use simple geometry or trigonometry to obtain the intersection point. Anyway, your solution is also a nice one.
One way to solve this is through a clever use of Cauchy-Schwarz Inequality.
First complete the squares to get ( x − 7 ) 2 + ( y − 3 ) 2 = 6 4 .
Our left hand side looks like the "greater than" side of the cauchy inequality. Since we want 3 x + 4 y , multiply by 3 2 + 4 2 to get 6 4 = ( ( x − 7 ) 2 + ( y − 3 ) 2 ) ( 3 2 + 4 2 ) ≥ ( 3 ( x − 7 ) + 4 ( y − 3 ) ) 2
6 4 ( 3 2 + 4 2 ) ≥ ( 3 x + 4 y − 3 3 ) 2
8 2 ∗ 5 2 ≥ ( 3 x + 4 y − 3 3 ) 2
4 0 ≥ 3 x + 4 y − 3 3
3 x + 4 y ≤ 7 3
With equality when the terms are linearly dependent. Namely, 3 x − 7 = 4 y − 3 . Using the original equation, equality is reached at ( 5 5 9 , 5 4 7 ) .
x 2 + y 2 = 1 4 x + 6 y + 6 ⇒ ( x − 7 ) 2 + ( y − 3 ) 2 = 6 4 . Let : x ′ = x − 7 y ′ = y − 3 ⇒ x ′ 2 + y ′ 2 = 6 4 We can find unique numbers r > 0 and 0 ≤ θ < 3 6 0 for which : x ′ = r c o s ( θ ) y ′ = r s i n ( θ ) ⇒ x ′ 2 + y ′ 2 = r 2 c o s 2 ( θ ) + r 2 s i n 2 ( θ ) = r 2 ( c o s 2 ( θ ) + s i n 2 ( θ ) ) = r 2 r 2 = 6 4 ⇒ r = 8 ,the only root since r>0 .
3 x + 4 y = 3 ( x ′ + 7 ) + 4 ( y ′ + 3 ) = 3 x ′ + 4 y ′ + 3 3 = 3 ∗ 8 c o s ( θ ) + 4 ∗ 8 s i n ( θ ) + 3 3 8 ( 3 c o s ( θ ) + 4 s i n ( θ ) ) + 3 3 We can find r’ and φ : 3 = r ′ s i n ( φ ) 4 = r ′ c o s ( φ ) ⇒ r ′ = 3 2 + 4 2 = 5 ⇒ 8 ( 5 s i n ( φ ) c o s ( θ ) + 5 c o s ( φ ) s i n ( θ ) ) + 3 3 = 4 0 ( s i n ( φ ) c o s ( θ ) + c o s ( φ ) s i n ( θ ) ) + 3 3 = 4 0 s i n ( θ + φ ) + 3 3 .The maximum value is reached when s i n ( θ + φ ) = 1 ,and that value is : 7 3
Consider the set of lines 3 x + 4 y = C .
Obviously there are infinitely many of these lines that intersect the circle x 2 + y 2 = 1 4 x + 6 y + 6 .
Simplifying the circle equation, we have ( x − 7 ) 2 + ( y − 3 ) 2 = 6 4 .
Now looking back at our set of lines, we see it is simply the set of all lines with slope − 4 3 .
Since linear functions have their maxima at their extrema, our solution line must be one of the two lines with slope -3/4 that is tangent to our circle. (Visualizing and applying common sense, it is clearly the tangent near the upper right corner of the circle).
Solving, we find the equation of the tangent line is 3 x + 4 y = 7 3 .
step 1) Differentiate the given equation w. r. t. x to get the value of dy/dx in terms of x and y. step 2) Put dy/dx = -3/4. Get the equation 4x - 3y = 19. step 3) Let k be the maximum value of 3x + 4y. Solve this with 4x - 3y = 19. Get x and y in terms of k. x = (3k + 76)/25 and y = (4k - 57)/25 step 4) Pur these values of x and y in the given equation. Get quadratic eqn in k. It is k^2 - 66k - 511 = 0. step 5) Solve this quadratic equation. One value is minimum of 3x + 4y. The other value is the maximum of 3x + 4y. This value is 73. Thus solved.
Changing x^{2} +y^{2} = 14x+6y+6 we get (x-7)^2 + (y-3)^2 = 8^{2} which represent equation of circle with center (7,3) and radius 8
For maximum value of 3x+4y : The line 3x+4y=k should be farthest distance from center and touch the circle.
The line passing through (7,3) and parallel to 3x+4y= k is 3x+4y = 33 The farthest distance from center of circle is 8
(|k-33|)/5 = 8
K= 73
Suppose, the equation x 2 + y 2 = 1 4 x + 6 y + 6 is a equation of circle.
Then we can rewrite the equation as ( x − 7 ) 2 + ( y − 3 ) 2 = 8 2
Converting this into the parametric form gives us - x = 7 + 8 c o s θ and y = 3 + 8 s i n θ
Now, let A = 3 x + 4 y . Plugging the parametric form in this equation gives us - A = 2 1 + 2 4 c o s θ + 1 2 + 3 2 s i n θ = 3 3 + 2 4 c o s θ + 3 2 s i n θ
Now, on taking the derivative of A w.r.t θ ,and putting it equal to 0 , we get t a n θ = 3 4
On taking the second derivative, we also find that this value ( t a n θ = 3 4 ) will give us the maximum value of A . Thus, we get maximum of A = 3 3 + 2 4 c o s θ + 3 2 s i n θ at s i n θ = 5 4 and c o s θ = 5 3 .
Plugging, these values back in A , we find A m a x = 3 3 + 5 7 2 + 5 1 2 8 = 7 3
But this is an Algebra problem. Let us solve it using Algebra.
x 2 + y 2 ⇒ x 2 − 1 4 x + 4 9 + y 2 − 6 y + 9 ( x − 7 ) 2 + ( y − 3 ) 2 = 1 4 x + 6 y + 6 = 6 + 4 9 + 9 = 6 4
Using Cauchy-Schwartz inequality, we have:
[ 3 ( x − 7 ) + 4 ( y − 3 ) ] 2 ⇒ [ 3 ( x − 7 ) + 4 ( y − 3 ) ] 2 ⇒ 3 ( x − 7 ) + 4 ( y − 3 ) 3 x − 2 1 + 4 y − 1 2 3 x + 4 y 3 x + 4 y ≤ ( 3 2 + 4 2 ) [ ( x − 7 ) 2 + ( y − 3 ) 2 ] ≤ ( 2 5 ) ( 6 4 ) ≤ ( 5 ) ( 8 ) ≤ 4 0 ≤ 4 0 + 2 1 + 1 2 ≤ 7 7
Let 3x+4y=a. We have to find the max value for a. This is the equation of a straight line with slope -3/4.
As we keep on increasing 'a', the straight line will go farther from origin.
Now, the equation given is a circle with centre (7,3) and radius 8.
Hence we need that straight line which is a tangent to this circle. So, as the radius line to a tangent is perpendicular to it, the slope of the line passing through (7,3) and our required point is 4/3.
So, we find that point on the circle which lies on the line through (7,3) and slope 4/3.
this is a circle........just write the equation of the tangent to it with a slope of -0.75.......... .....write eqn of tangent in slope form......it will automatically give .3x+4y=73.........it also gives the minimum value as -7
( x − 7 ) 2 + ( y − 3 ) 2 = 6 4 3 x + 4 y = 3 ( x − 7 ) + 4 ( y − 3 ) + 2 1 + 1 2 Use Cauchy-Schwarz Inequality 3 x + 4 y = < s q r t ( 3 2 + 4 2 ) s q r t ( ( x − 7 ) 2 + ( y − 3 ) 2 ) + 2 1 + 1 2 = < 5 ( 8 ) + 2 1 + 1 2 = 7 3
The slope of the tengent to the circle at point (x,y) will follow the equation: − ( y − 3 ) ( x − 7 ) and should be equal to the slope of 3x+4y=C for maximum value of "C" hecne − ( y − 3 ) ( x − 7 ) = − 4 3 hence put the value of x − 7 = 4 3 × ( y − 3 ) in equation of circle (which having a center of (7,3)) and find X and Y it will be 59/5 and 47/5 respectively hence the ans is 73
x=7+8cos(t) y=3+8sin(t)
max 3x+4y = 24cost(t) + 32sin(t) + 33
At max tan(t) = 4/3 sin(t) = 4/5 cost(t) = 3/5
Hence max is 73
From the prob. We get ( x − 7 ) 2 + ( y − 3 ) 2 = 6 4 From Cauchy [ ( x − 7 ) 2 + ( y − 3 ) 2 ] [ 9 + 1 6 ] > = [ 3 ( x − 7 ) + 4 ( x − 3 ) ] 2 Then ( 6 4 ) ( 2 5 ) > = ( 3 x + 4 y − 3 3 ) 2 4 0 > = 3 x + 4 y − 3 3 7 3 > = 3 x + 4 y Answer 7 3
very good. This is much shorter than my solution. I appreciate it!
We can write the equation as (x-7)^2 + (y-3)^2 = 8^2 so x = 8sinA + 7, y = 8cosA + 3
So 3x + 4y = 8(3sinA + 4cosA) + 33 <= 8x5 + 33 = 73
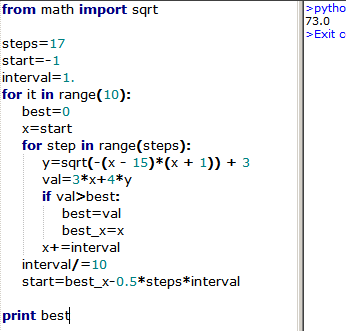
Rearranging the given equation, we get,
( x − 7 ) 2 + ( y − 3 ) 2 = 6 4
Hence, we can substitute,
x = 7 + 8 cos θ
y = 3 + 8 sin θ
We are required to evaluate the maximum value of 3 x + 4 y
Thus, we find the maximum of 3 3 + 2 4 cos θ + 3 2 sin θ ,
which is clearly 3 3 + 2 4 2 + 3 2 2 = 7 3