Underwater Magnification
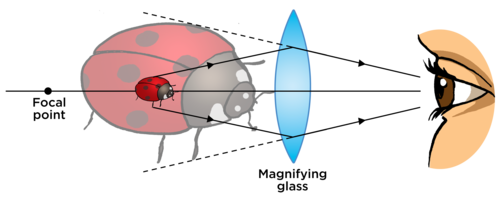
A magnifying glass is a convex lens. It makes a nearby object look bigger by converging light rays.
Now suppose you look at the same object with the magnifying glass while underwater, keeping the distance between the object and the lens fixed. How would it appear?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
The diagram nicely explains it. The glass lens converges light less underwater, so the image appears smaller.
What would happen if we had used a concave lens instead of a convex lens?
Log in to reply
If we had used a concave instead of a convex lens, than the object would seem bigger underwater than in the air (although both images - in air and underwater - would look smaller than original object). Logic is the same as for convex lens: concave lens will diverge light less underwater than in the air, resulting image to appear bigger.
Log in to reply
Thanks, I have corrected my comment.
If the refractive index of the surrounding becomes greater than the refractive index of the medium, the concave lens would make a nearby object appear larger than it actually is.
Log in to reply
@Pranshu Gaba – Exactly! Here's the picture:
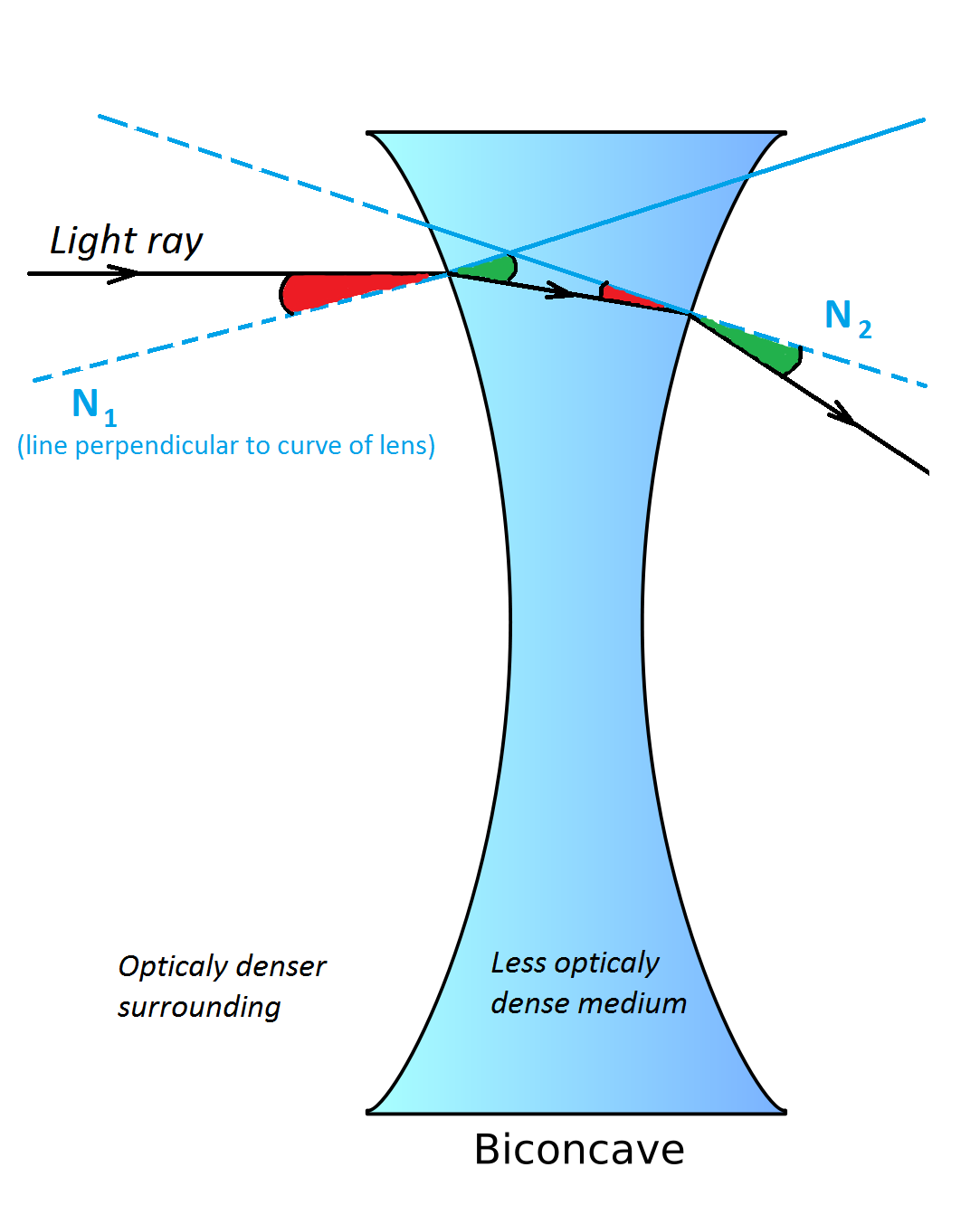
When light goes from optically denser to less dense surrounding, it's direction shifts away from the line perpendicular to boundary between these two surroundings, resulting angle of incidence to be smaller than the angle of refraction (as shown in the picture). If surrounding was denser than medium (lens), concave lens would actually converge light and the object would appear larger.
The diagram is not quite accurate, and therefore slightly misleading. The light does not change direction once in the middle of the lens, it changes direction twice as it enters and leaves the lens. This is an important aspect of the diagram because the answer depends on how much the light changes direction as it moves from one medium to another.
Log in to reply
I've just taken the original problem image and added a few new lines and, although I agree that it is not quite correct representation, I believe that it doesn't affect much general idea behind the solution.
Relevant wiki: Lenses
This question is ill-posed. You can make the image smaller or bigger by changing the distance to the object or to the eye. The thin lens imaging equation is: s 1 + i 1 = f 1 and the magnification is M = − s i , where s is the source distance, i is the image distance, and f is the focal length.
What can be said is: the focal length f will be longer when it is placed in water because Lens maker's equation is: f 1 = ( n a m b i e n t n l e n s − 1 ) × ( R f 1 − R b 1 ) where n l e n s ≈ 1 . 5 for glass, n a m b i e n t = 1 . 0 or 1 . 3 3 for air or water, respectively, and R f and R b are the radii of curvature of the front and back of a thin lens (fixed). Or, more intuitively, we can say that the lens bends light at a smaller angle in water than in air.
If the source distance is fixed, the longer focal length implies the image distance needs to be longer and so the magnification would be greater in water. If the image distance is fixed, then the source distance needs to be longer and the magnification would be smaller. And if both are adjusted, it's possible to keep their ratio constant and have the same magnification. So, what is being changed when viewing under water needs to be stated for this problem to be properly posed.
Ill-posed problem. How much of the system is under water?
Log in to reply
The entire system, including the lens and the object, is underwater.
I used a normal magnifying glass and tried it out in the bath and the object looked bigger than just using the magnifying glass outside the bath, is a normal magnifying glass different to the one described?
Log in to reply
Did you put your head underwater as well? Since the eye is part of the system it would need to be submersed as well.
Thanks for the solution. Indeed, for a given lens we can adjust the magnification by moving the source or by changing the refractive index of the surrounding medium compared to the lens.
In this problem, I meant that the entire setup is immersed in water without changing the position of the object or the lens. I have edited the problem statement to clarify this.
The question is unclear whether or not the observer, lens, and object are ALL under water.
water = denser than air, hence light rays converging to eyes will refract lesser than they do in air.
which will result in smaller image when we make virtual lines from them
I thought you meant the viewer was under water and viewing the same, but through the different media. In that case, Inthinknit is the same size as if viewed out if the water.
Log in to reply
yep, viewer is underwater and whole is underwater too i.e., replace air with water in the diagram
ratio glass:air > ratio glass:water. smaller than seen in air
Relevant wiki: Lenses
When a light ray enters a different medium, its direction changes. The greater optical density difference between two mediums, the greater the change in direction will be. We know that the glass is denser than the air, as well as water, so the difference between optical density of water and glass is smaller than between air and glass. Thus, the change of direction of light rays will be smaller and hence, the object will look smaller than it looks in the air (if you didn't understand last sentence, just carefully examine the picture).
Sorry for my simplified English, maybe I haven't got right all the terms, but that's because I studied optics only in Serbian.