Unequal rods Oscillations

The kinetic energy of the system is $T \; = \; \tfrac12I_1\dot{\theta}_1^2 + \tfrac12I_2\dot{\theta}_2^2 \; = \; \tfrac13\dot{\theta}_1^2 + \tfrac16\dot{\theta}_2^2 \; = \; \tfrac12\dot{u}^2 + \tfrac13\dot{u}\dot{v} + \tfrac12\dot{v}^2$ where $u = \tfrac12(\theta_1 + \theta_2)$ and $v = \tfrac12(\theta_1 - \theta_2)$ . The length of the spring is $2\cos\tfrac12(\theta_1 + \theta_2) = 2\cos\,u$ , and so the potential energy of the system is $V \; = \; \tfrac12K(2\cos u - 1)^2 \; = \; 10(2\cos u - 1)^2$ Thus the Lagrangian for the system is $\mathcal{L} = \tfrac12\dot{u}^2 + \tfrac13\dot{u}\dot{v} + \tfrac12\dot{v}^2 - 10(2\cos u - 1)^2$ and so Lagrange's equations give $\tfrac13\ddot{u} + \ddot{v} \; = \; \frac{d}{dt}\left(\frac{\partial \mathcal{L}}{\partial \dot{v}}\right) \; =\; \frac{\partial \mathcal{L}}{\partial v} \; = \; 0$ and $\tfrac89\ddot{u} \; = \; \ddot{u} + \tfrac13\ddot{v} \; = \; \frac{d}{dt}\left(\frac{\partial \mathcal{L}}{\partial \dot{u}}\right) \; =\; \frac{\partial \mathcal{L}}{\partial u} \; = \; \frac{\partial}{\partial u}\left(-10(2\cos u - 1)^2\right)$ from which we deduce that $\tfrac49 \dot{u}^2 + 10(2\cos u - 1)^2 \; = \; 10(2\cos u_0 - 1)^2$ where $u_0$ is the initial value of $u$ . We want to evaluate $A = 2\dot{u}^2$ . For the given initial and final angle values we obtain $A = \boxed{2.643450205}$ .

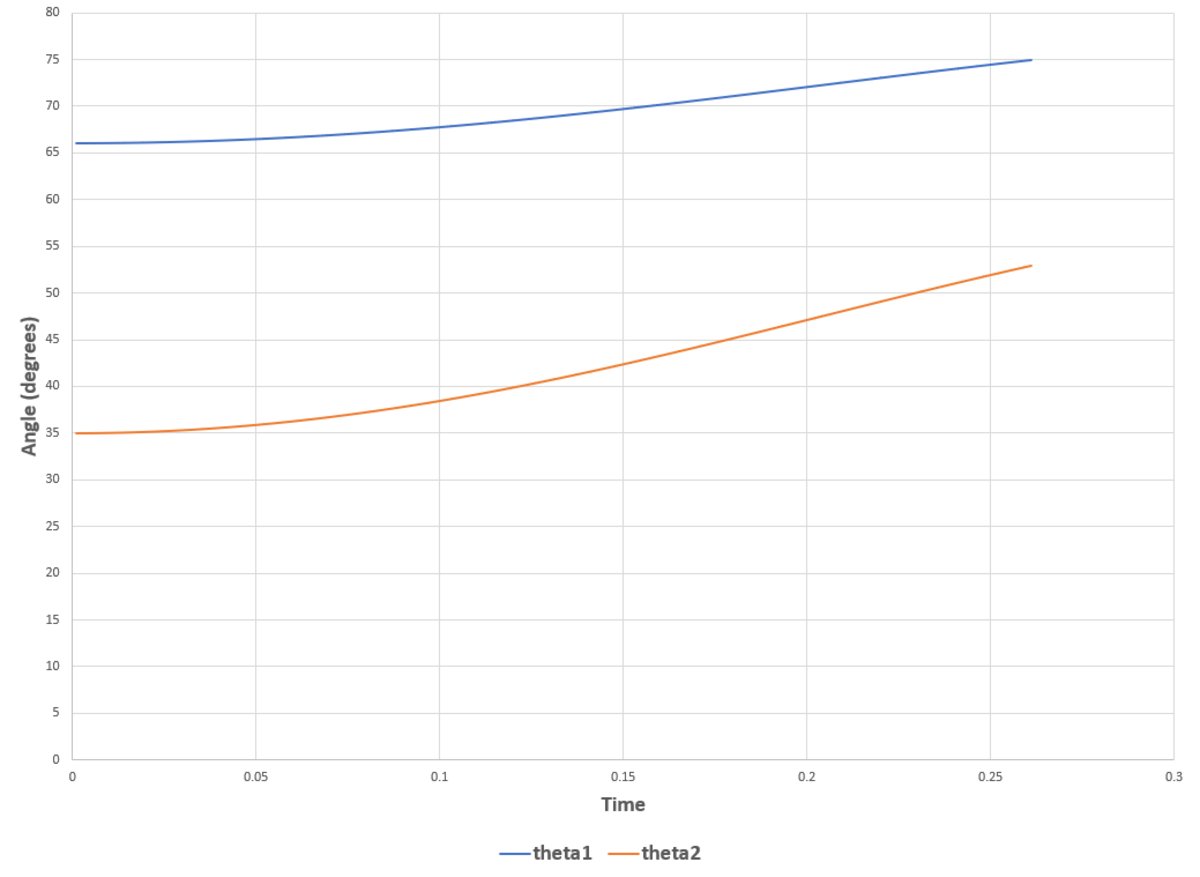
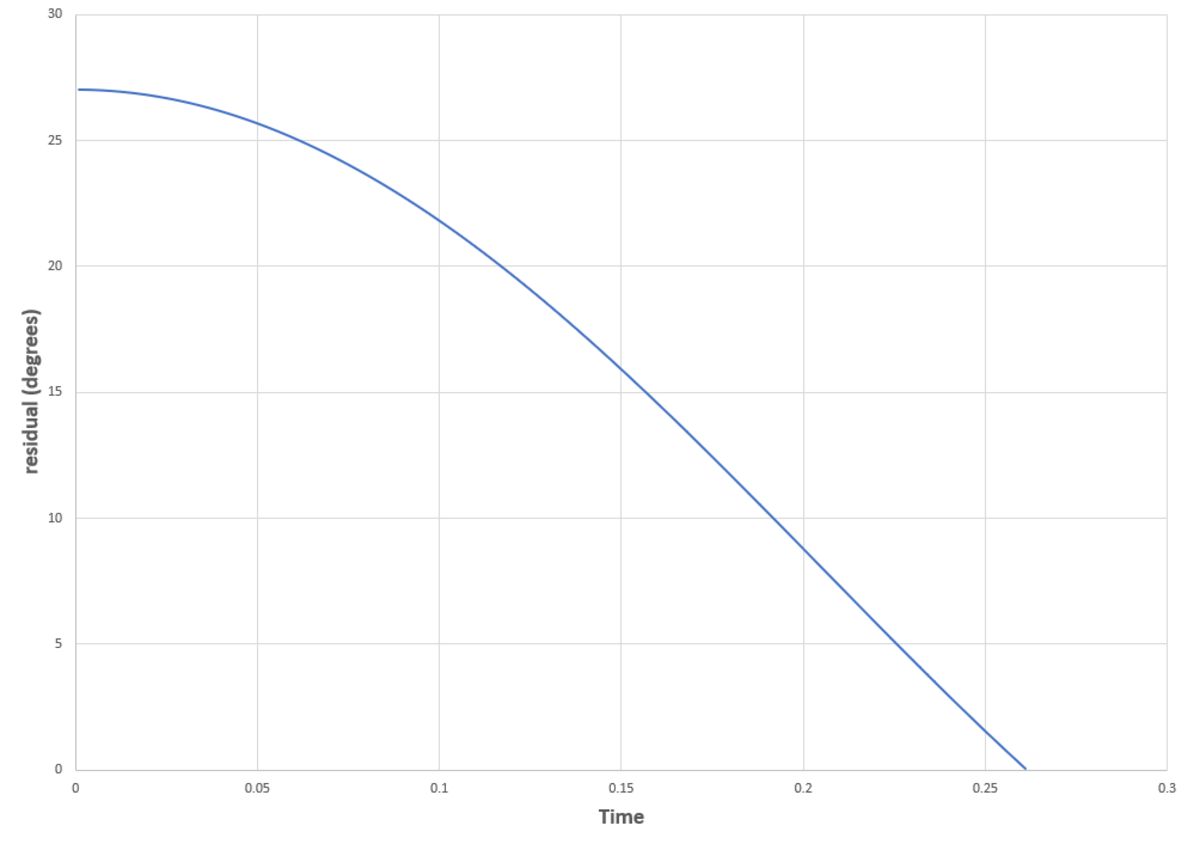
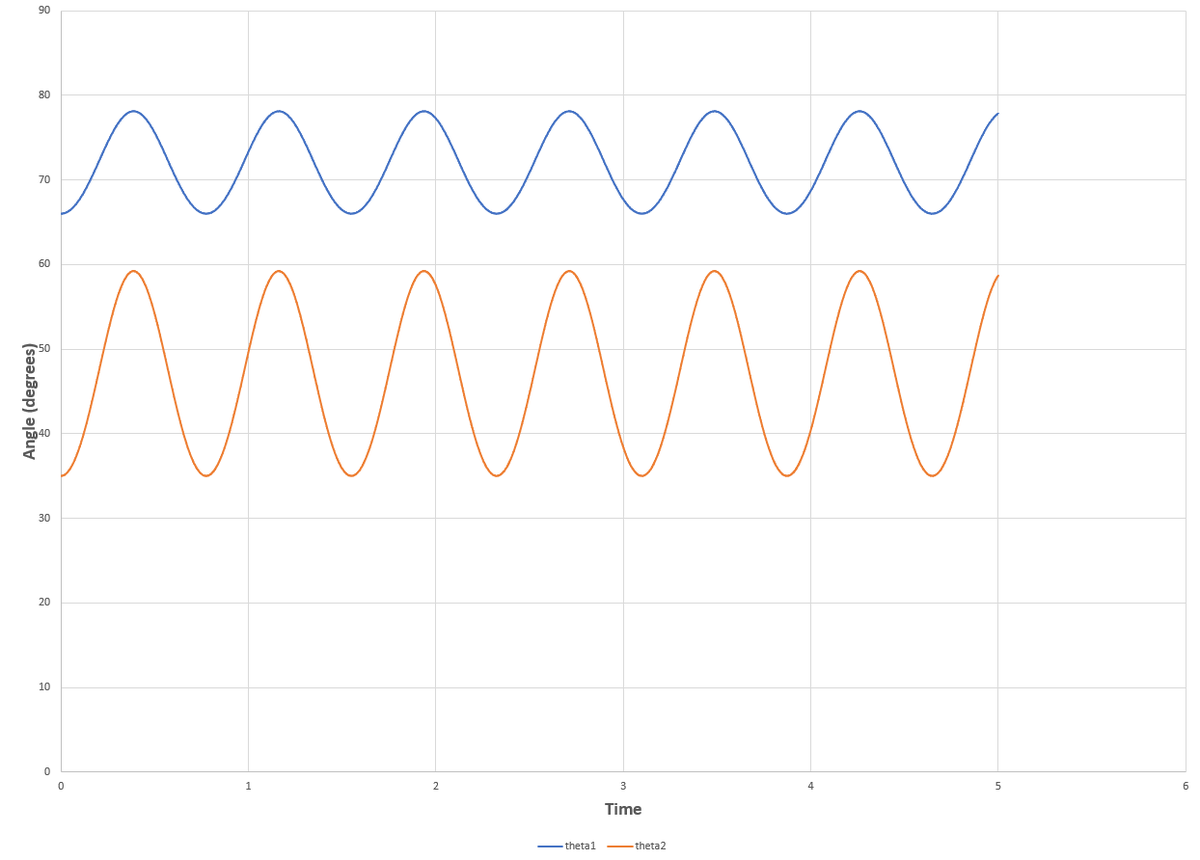
Admittedly, I did not solve analytically. I modified the code from the original problem to solve numerically for the time dynamics. The simulation runs until the "residual" becomes zero. The residual is calculated as $|\theta_1 - \theta_{1f}| + |\theta_2 - \theta_{2f}|$ , where $\theta_{1f}$ and $\theta_{2f}$ are the given angles at which to evaluate the $A$ quantity. The most challenging thing about this problem for me was keeping the conventions straight. The code actually references both angles to the positive $x$ axis. With that reference $\dot{\theta}_2$ is negative at the end, but with respect to the negative $x$ axis, $\dot{\theta}_2$ is positive. I used up two tries just on convention errors before straightening everything out. Below are plots of the angles over time (as referenced in the diagram), and of the residual (in degrees) over time. You can see that both angles increase, meaning that the rods are pulling together. Running the simulation for longer (third plot) shows sinusoidal oscillations in the angles, which have the same frequency and the same phase, but different magnitudes.

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135

import math
import random

# Constants

deg = math.pi/180.0

g = 10.0

k = 20.0
L0 = 1.0

m1 = 2.0
L1 = 1.0

m2 = 1.0
L2 = 1.0

I1 = (1.0/3.0)*m1*(L1**2.0)
I2 = (1.0/3.0)*m2*(L2**2.0)

theta1f = 75.0115 * deg
theta2f = (180.0 - 53.0229) * deg

res_thresh = 0.0001 * deg

dt = 10.0**(-6.0)

#################################

res = 99999999.0

t = 0.0

theta1 = 66.0 * deg
theta2 = (180.0 - 35.0) * deg

theta1d = 0.0
theta2d = 0.0

theta1dd = 0.0
theta2dd = 0.0

count = 0

print "t theta1 theta2 res"

while res > res_thresh:               # primary loop condition
#while t < 5.0:                               # alternate loop condition
    theta1 = theta1 + theta1d * dt    # numerical integration
    theta2 = theta2 + theta2d * dt

    theta1d = theta1d + theta1dd * dt
    theta2d = theta2d + theta2dd * dt

    x1 = L1*math.cos(theta1)  # rod end points
    y1 = L1*math.sin(theta1)

    x2 = L2*math.cos(theta2)
    y2 = L2*math.sin(theta2)

    Dx = x2 - x1  # vector between rod end points
    Dy = y2 - y1

    D = math.hypot(Dx,Dy)

    ux = Dx/D   # unit vector between rod end points
    uy = Dy/D

    s = D - L0  # stretch
    Fs = k*s   # spring force magnitude

    Fs1x = Fs*ux  # spring force on rod 1
    Fs1y = Fs*uy

    Fs2x = -Fs1x  # spring force on rod 2
    Fs2y = -Fs1y

    r1x = x1  # lever arm for spring force on rod 1
    r1y = y1

    r2x = x2   # lever arm for spring force on rod 2
    r2y = y2

    Fg1x = 0.0     # gravity forces (zeroed out)
    Fg1y = -m1*g*0.0

    Fg2x = 0.0
    Fg2y = -m2*g*0.0

    T1s = r1x*Fs1y - r1y*Fs1x   # spring torques
    T2s = r2x*Fs2y - r2y*Fs2x

    T1g = (r1x/2.0)*Fg1y - (r1y/2.0)*Fg1x  # gravity torques
    T2g = (r2x/2.0)*Fg2y - (r2y/2.0)*Fg2x

    T1 = T1s + T1g  # net torques
    T2 = T2s + T2g

    theta1dd = T1/I1   # angular acceleration
    theta2dd = T2/I2   

    res = math.fabs(theta1-theta1f) + math.fabs(theta2-theta2f)   # keep track of angle differences from final values

    t = t + dt
    count = count + 1

    if count%1000 == 0:
        print t,(theta1/deg),(180.0-theta2/deg),(res/deg)


#################################

print ""
print ""

A = ((theta1d - theta2d)**2.0)/2.0

print dt
print (res_thresh/deg)
print t
print ""
print theta1d
print theta2d
print ""
print A

#1e-06
#0.0001
#0.261501

#0.76644906543
#-1.53289813086

#2.64349876454

An analytical approach is as follows. Usually, problems like these cannot be solved analytically. However, in this case, we are lucky to see some structure in the equations of motion which can be exploited.

Notice how the spring and the two rods form a triangle. More specifically, an isosceles triangle. This is because of the rods having an equal length. From here, two equations can be formed by calculating the torque about the origin.

The angle between either rod and the spring is:

$\phi = \frac{\theta_1 + \theta_2}{2}$

The above result follows from elementary geometry. Now the torque experienced by rod 1 about the origin is:

$T_1 = F_s L_1 \sin{\phi} = I_1 \ddot{\theta}_1$

The torque experienced by rod 2 about the origin is:

$T_2 = F_s L_2 \sin{\phi}=I_2 \ddot{\theta}_1$

Here,

$F_s = K\left(\sqrt{\left(\cos{\theta_1}+\cos{\theta_2}\right)^2 + \left(\sin{\theta_2}-\sin{\theta_1}\right)^2} - 1\right)$ $I_1 = \frac{1}{3}{m_1 L_1^2}$ $I_2 = \frac{1}{3}{m_2 L_2^2}$

Now, by simplifying the two equations of motion by using trigonometric identities (steps omitted), we get:

$\ddot{\theta}_1=\frac{15\,\sqrt{2}\,\sin\left(\theta _{1}+\theta _{2}\right)\,\left(\sqrt{2}\,\sqrt{\cos\left(\theta _{1}+\theta _{2}\right)+1}-1\right)}{\sqrt{\cos\left(\theta _{1}+\theta _{2}\right)+1}}$

$\ddot{\theta}_2= \frac{30\,\sqrt{2}\,\sin\left(\theta _{1}+\theta _{2}\right)\,\left(\sqrt{2}\,\sqrt{\cos\left(\theta _{1}+\theta _{2}\right)+1}-1\right)}{\sqrt{\cos\left(\theta _{1}+\theta _{2}\right)+1}}$

Adding the two equations above gives:

$\ddot{\theta}_1+\ddot{\theta}_2 = \frac{45\,\sqrt{2}\,\sin\left(\theta _{1}+\theta _{2}\right)\,\left(\sqrt{2}\,\sqrt{\cos\left(\theta _{1}+\theta _{2}\right)+1}-1\right)}{\sqrt{\cos\left(\theta _{1}+\theta _{2}\right)+1}}$

Let $\theta_1 + \theta_2 = z$ . Then, by substituting this expression in the above result gives:

$\ddot{z} = \frac{45\,\sqrt{2}\,\sin\left(z\right)\,\left(\sqrt{2}\,\sqrt{\cos\left(z\right)+1}-1\right)}{\sqrt{\cos\left(z\right)+1}}$

This can be rewritten as:

$\dot{z}\frac{d\dot{z}}{dz} = f(z) = \frac{45\,\sqrt{2}\,\sin\left(z\right)\,\left(\sqrt{2}\,\sqrt{\cos\left(z\right)+1}-1\right)}{\sqrt{\cos\left(z\right)+1}}$

Separating the variables, applying initial conditions and integrating gives:

$\frac{\dot{z}^2}{2} = \frac{\left(\dot{\theta_1}+\dot{\theta_2}\right)^2}{2} = \int_{a}^{b} f(z) dz$

Where $a = \frac{\pi}{180}\left(66+35\right)$ and $b = \frac{\pi}{180}\left(75.0115+53.0229\right)$

The integral has a closed-form expression but the calculations are a bit tedious given the weird limits of integration. I have left out the steps to solve this integral. The last step was done using a calculator giving the answer of:

$\boxed{A = \frac{\left(\dot{\theta_1}+\dot{\theta_2}\right)^2}{2} \approx 2.6435}$

Although I have left out a few steps, I will elaborate further if requested.