Unforeseen Chaos
This is a follow-up question to this problem.
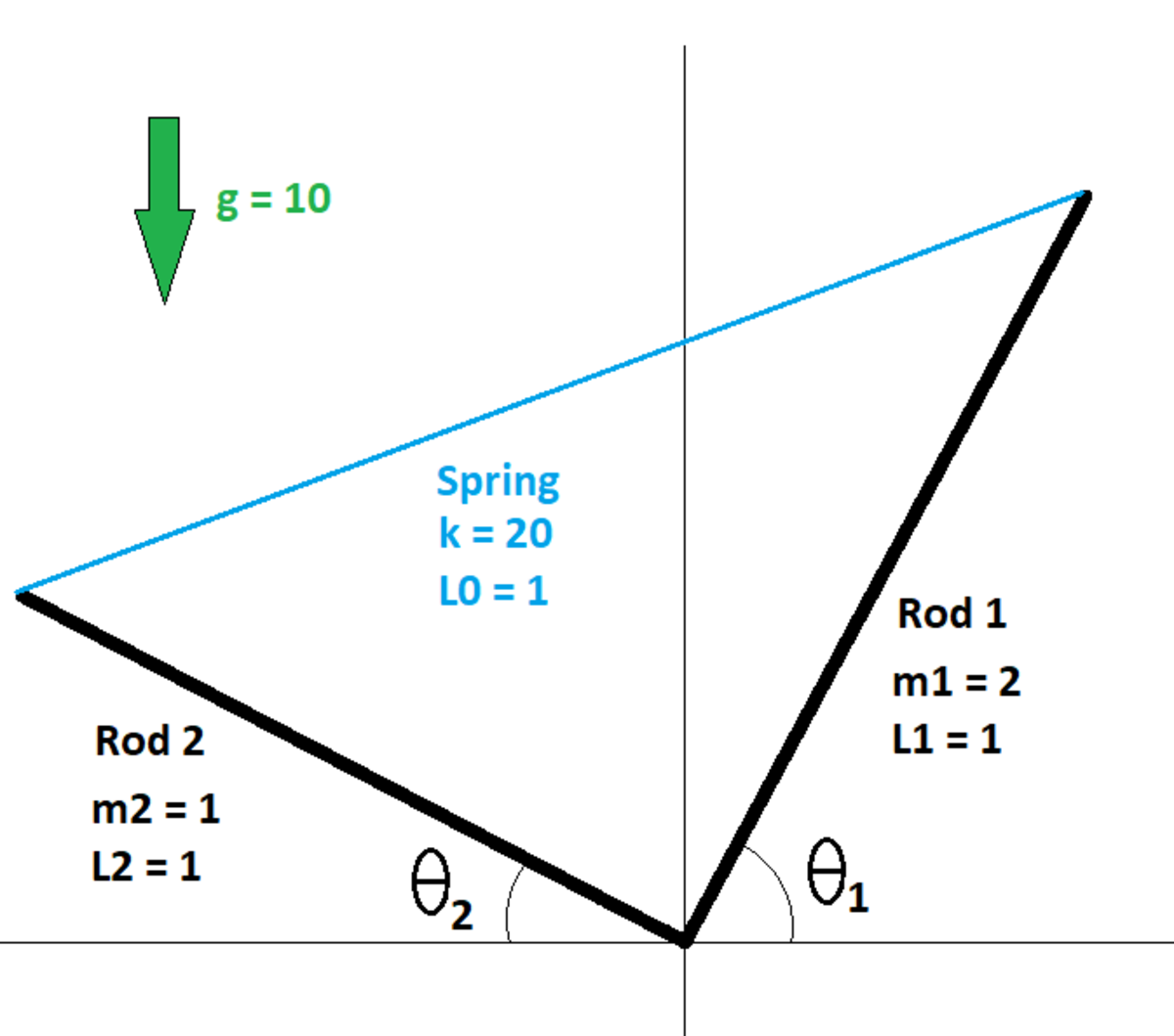
Two uniform rods are hinged about the origin. Each rod can rotate about the Z axis independently of the other (the axis being perpendicular to the page). The other ends of both rods are connected by a spring. The diagram shows the masses and lengths of both rods, the force constant and natural length of the spring, and the ambient gravitational acceleration.
The system is released from rest at time t = 0 when θ 1 = 6 6 o and θ 2 = 3 5 o . Find the following quantity A at t = 3 s .
A = 2 ( θ ˙ 1 + θ ˙ 2 ) 2
In the quantity A , the angular velocities are in rad/s.
Note: I encourage the solver to try the following:
- Simulate the system for more than 40 seconds. Perform simulations at different time steps (for a given set of initial conditions) and compare each case with the other.
- Formulate the equations of motion differently (Newtonian/ Lagrangian) and then repeat the first suggestion. It seems like the structure of the equations influences the outcome. Is this expected?
- Try different initial conditions. Even for different formulations of the equations of motion. Is something weird going on?
- Think about what does this dynamic system qualify as and why? How is it different from the case when gravity is not accounted for, as in the previous problem?
Also note: At no point of time do the rods collide with each other. Analyse the system with the given information and focus on the resulting dynamics only.
I look forward to having some fruitful discussions on your findings in the comment section.
The answer is 0.1841.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Right now, I wish I could up-vote the 'Brilliant' option twice. Very nicely explained! Thanks for sharing.
Thanks much. I enjoyed the followup problems. One thing I would like to know is whether or not we can determine a-priori whether a system is likely to behave chaotically, by looking at the governing equations for that system. In other words, is there a "chaos signature" that we can see in advance?
Log in to reply
Well, I have heard of a concept of 'Lyapunov exponents' but I have not deep-dived into it. It helps qualify a system as chaotic, mathematically. This is all I know at this stage.
Furthermore, when any dynamic system (mechanical or electrical) is written in its state-space form, the resulting system of differential equations must be non-linear and be at-least of order 3. If these conditions are satisfied, the system may be chaotic. While this is not a sufficient condition for chaos, it does tell us that lower-order systems (<3) and linear systems can never be chaotic.
The numeric integration is certainly sensitive to the interval, but is the behaviour here chaotic? The double pendulum exhibits (deterministic) chaos because there are times when (in particular) the lower arm can become vertical - if it just reaches the vertical, does it continue on in the same direction, or swing back the other way? Minute changes in the initial conditions will effect which of these happens, and we get chaotic behaviour.
There will be cases here where the system may just pass through a position of static equilibrium, in which case chaos will ensue because small changes in initial conditions will determine "which side" of that equilibrium the system evolves into. Does that happen in this instance? I haven't checked.
Chaotic behaviour tends to be associated with nonlinear equations, but nonlinear equations are also good at generating rounding errors in numeric integration. Which is the villain here is an interesting question.
Log in to reply
Interesting question indeed. Whether it is a numerical issue or chaos can be resolved by computing a system's Lyapunov exponents. I read a little bit about the concept of Lyapunov exponents, after seeing your comment, and here is what I have understood. Please correct me if I am wrong. Consider an autonomous and continuous dynamic system:
x ˙ = F ( x )
Here, F is a continuous vector field on n dimensions. Consider this equation to have two solution trajectories by choosing initial conditions very close to each other. Let one solution be x 1 and the other solution is x 1 + δ . Both x 1 and δ are functions of time. So the investigation boils down to whether the separation between these two trajectories increases, decreases or remains constant over time.
Since x 1 + δ is a solution:
x ˙ 1 + δ ˙ = F ( x 1 + δ )
⟹ δ ˙ = F ( x 1 + δ ) − F ( x 1 )
Given that the solutions begin very close to each other, the term F ( x 1 + δ ) can be first-order Taylor series approximated about the trajectory x 1 to obtain:
δ ˙ = J δ
Where J is the jacobian matrix of the vector field F ( x ) evaluated at the initial separation between the two trajectories.
So whether nearby trajectories converge or diverge depends on the eigenvalues of the matrix J . A positive (real part) eigenvalue would indicate that the separation increases exponentially which is an indication of chaos. On applying this to the given system, I see positive eigenvalues which to me indicates chaos. I have not shown this calculation here, but you could try and give me feedback if possible.
Log in to reply
Consider the differential equation y ′ ( x ) = y ( x ) . This would mean that the (single) Lyapunov exponent in this case was 1 , but I don't think we would say that this system was chaotic. Some solutions naturally diverge from each other. I do not know much about Lyapunov exponents, but it seems more than positive eigenvalues are required to indicate chaos - "other conditions", such as a compact state space, are mentioned.
Numerical methods naturally eventually develop errors. If we tried to solve the above differential equation, with the initial condition y ( 0 ) = 1 , by the numerical method y n + 1 = y n + h y n ′ we would obtain y n = ( 1 + h ) n , so the estimate we would obtain for y ( x ) would be ( 1 + n x ) n , if we used n steps to get to x . For any fixed n , this estimate will diverge (exponentially) from e x as we let x increase. On the other hand, the solution tends to e x if we keep x fixed and let n tend to infinity.
Further thoughts. The static equilibrium position for this problem was with θ 1 = 6 6 . 0 5 4 ∘ and θ 2 = 3 5 . 7 3 3 ∘ . Testing initial values of θ 1 of 6 6 ∘ and 6 6 . 1 ∘ is likely to be pushing the problem near the "passing through a position of static equilibrium" state, and therefore we should expecting trajectories to diverge.
Would it not also be worthwhile running a more accurate numerical method, like Runge-Kutta? The Euler method you are using is much more prone to error. Using RK4, I obtain this plot (the horizontal axis is in milliseconds and the vertical in radians) for θ 1 and θ 2 with initial values of 6 6 ∘ and 3 5 ∘ . This is at least more approximately periodic, and does not get out of control (yet). Obviously we get a different graph for 6 6 . 1 ∘ , but that puts us the other side of the static equilbrium point, so that is no great surprise.
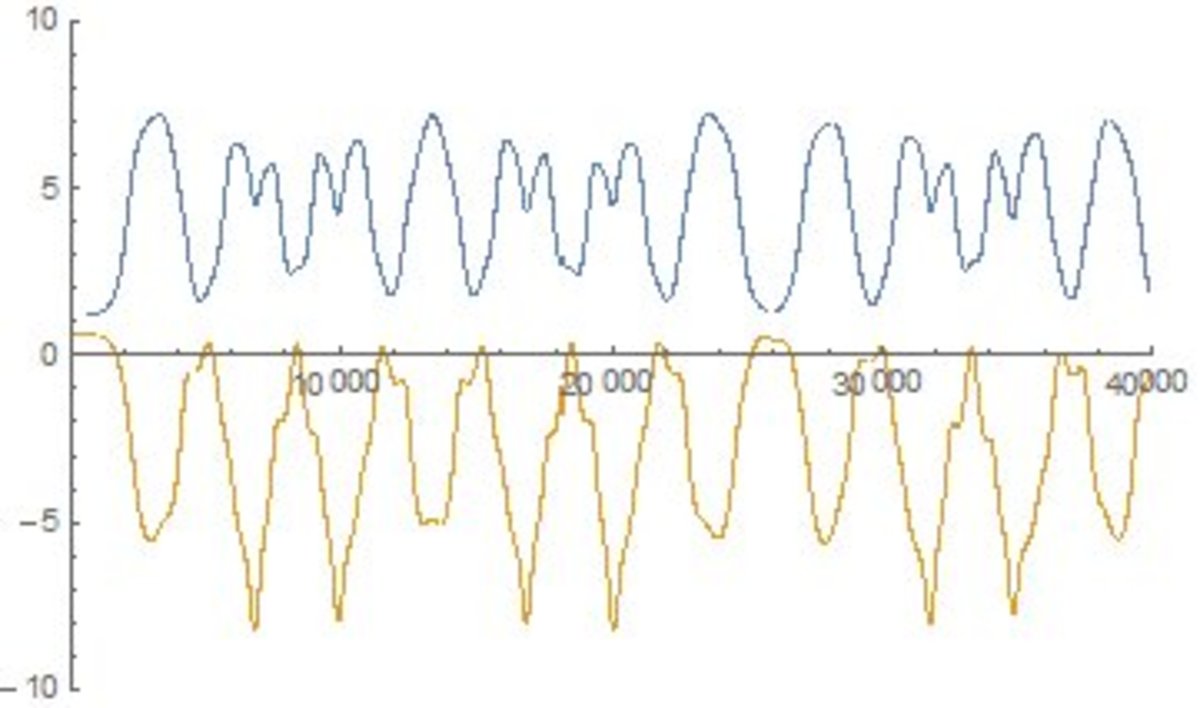
Log in to reply
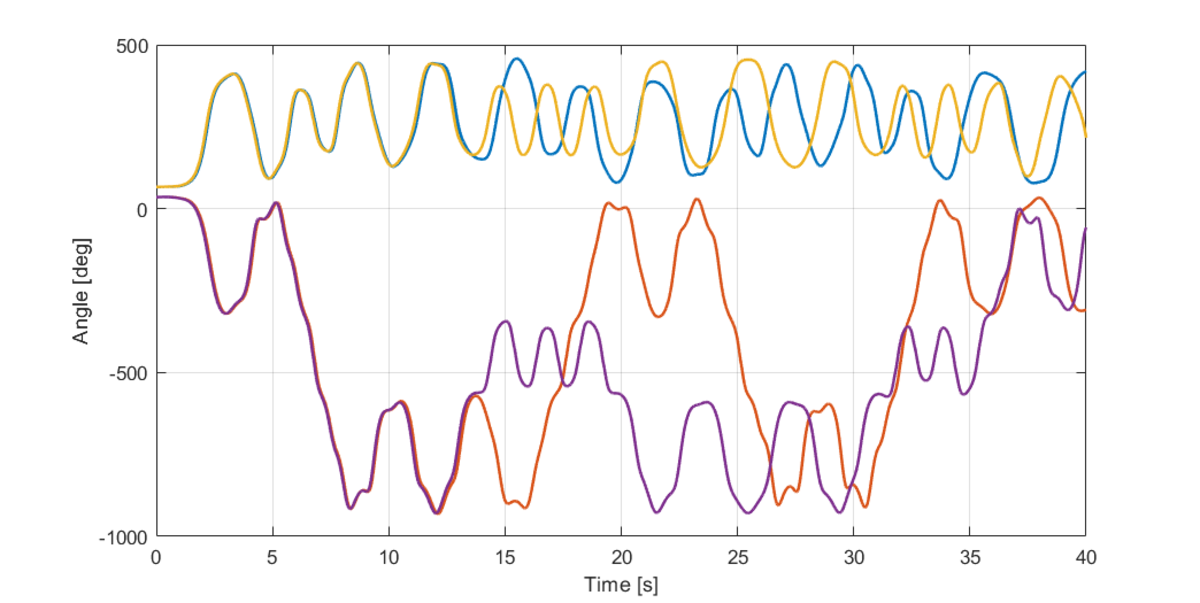
Thanks for sharing your insights. While framing this problem, I used the RK-4 method mostly. I quickly ran a simulation using RK-4 and the above plots are what I obtain. The angular responses are significantly different from that you have obtained.
I derived two forms of the equations of motion(EOM) and I ran the RK-4 solver using both. The first plot shows angular responses using one form while the second plot shows the response using the other form of the EOM. The solutions are quite different from the plot you have obtained. This is because apart from sensitive dependence on initial conditions, the solutions are dependent on the form of the differential equations too.
Even looking more carefully at your plot, while there seems to be some sort of periodicity, the behaviour does not repeat exactly in any consecutive intervals between 0 and 40 seconds.
Log in to reply
The above comment has been edited.
Speaking of passage through an equilibrium point, it is difficult to visualise what happens in that event given the unpredictability of the response.
Log in to reply
@Karan Chatrath – Well, if we introduce the variables u = 2 1 ( θ 1 + θ 2 ) and v = 2 1 ( θ 1 − θ 2 ) , the Lagragian of the system is L = 2 1 u ˙ 2 + 3 1 u ˙ v ˙ + 2 1 v ˙ 2 − 1 0 ( 2 cos u − 1 ) 2 − 1 0 sin ( u + v ) − 5 sin ( u − v ) and hence we obtain the differential equations u ¨ + 3 1 v ¨ 3 1 u ¨ + v ¨ = ∂ u ∂ L = 4 0 ( 2 cos u − 1 ) sin u − 1 0 cos ( u + v ) − 5 cos ( u − v ) = ∂ v ∂ L = − 1 0 cos ( u + v ) + 5 cos ( u − v ) and hence u ¨ v ¨ = 4 5 ( 2 cos u − 1 ) sin u − 1 5 cos u cos v = − 1 5 ( 2 cos u − 1 ) sin u + 1 5 sin u sin v together with the initial conditions u ( 0 ) = 3 6 0 1 0 1 π , v ( 0 ) = 3 6 0 3 1 π and u ˙ ( 0 ) = v ˙ ( 0 ) = 0 . The graph I posted initially was one I coded myself using RK4. Mathematica, which (presumably) knows what it is doing, gives this output for θ 1 and θ 2 when solving the above equations using NDSolveValue :
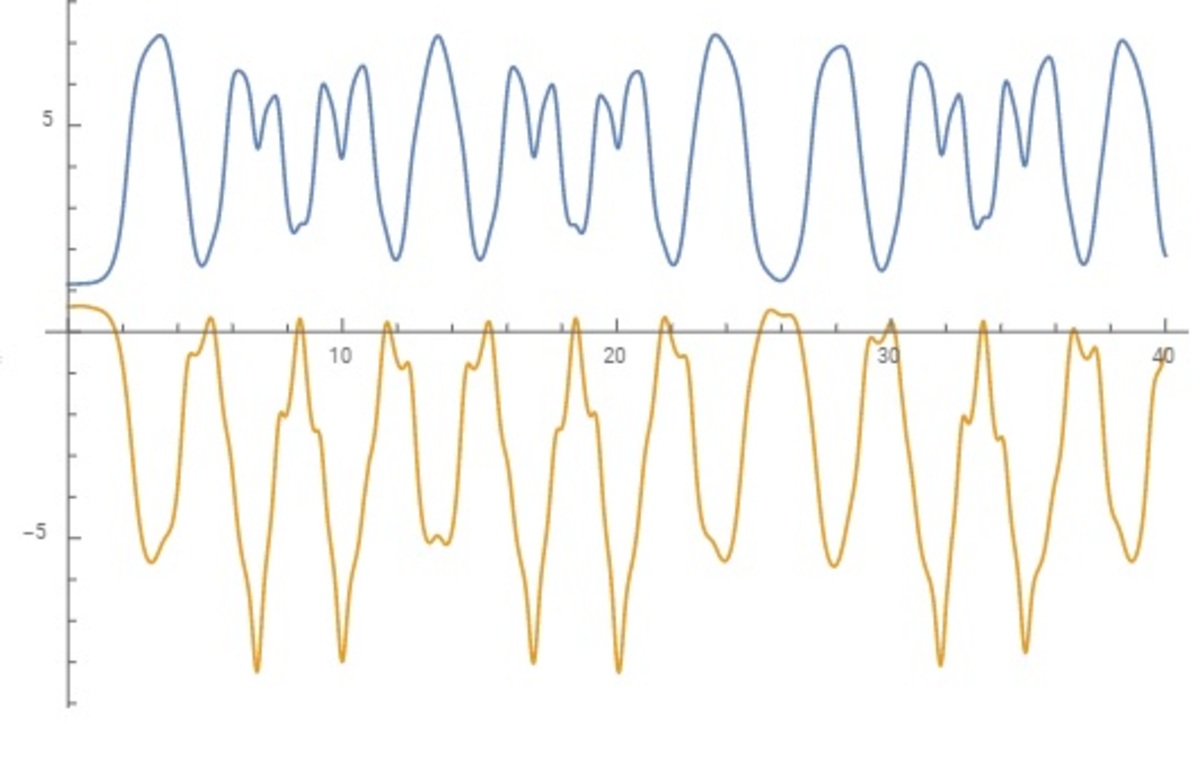
so my coded version is matched.
However, there are values of t for which θ 1 + θ 2 = π or − π , which means that the two rods do collide with each other, at which point the model becomes invalid...
Log in to reply
@Mark Hennings – Thank you for sharing your working. Nice approach to modelling the system. I took the system of differential equations that you obtained and re-ran the simulations using RK-4. The results are the same as that you obtain.
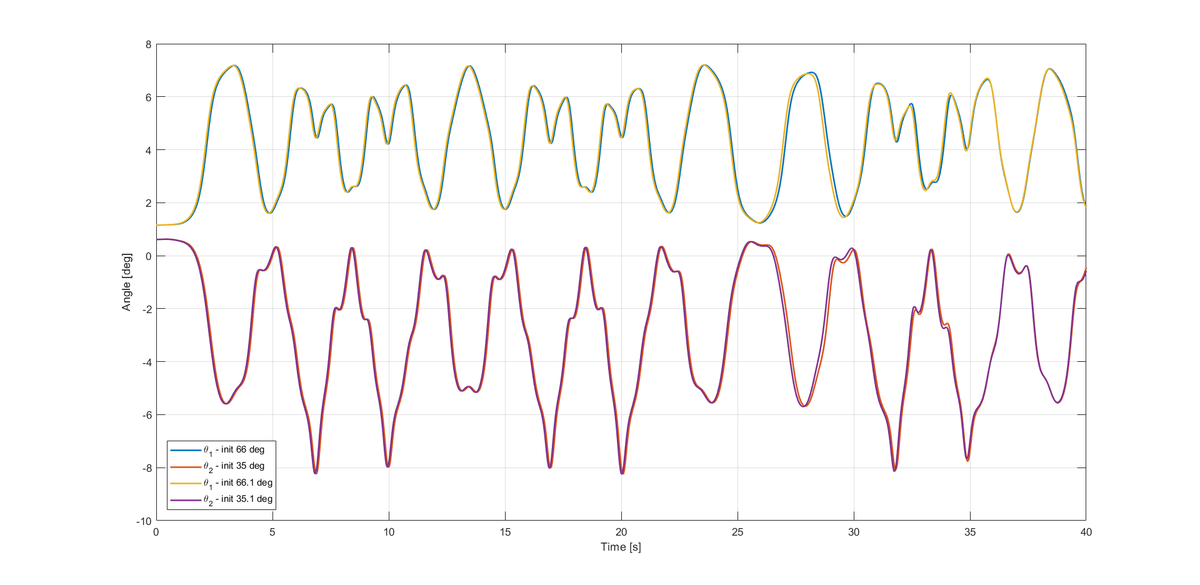
What is really remarkable here is that the solutions do not exhibit sensitivity to initial conditions. And this is in contrast with the solutions I plotted earlier.
I modelled the system using θ 1 and θ 2 as generalised coordinates. I obtained a form of the equations that is different from what you have. So the solutions are probably sensitive to the form of the differential equations, or my working is incorrect. I will revisit my solution again. But nevertheless, this is an interesting result and I now understand the possibility of the weird solutions being as a result of numerical errors and not necessarily chaos.
Indeed, looks like I would have needed to switch to a higher-order method to get good results farther out into the future. However, even with Euler, comparing results with time steps spanning orders of magnitude is a decent safeguard against bad results.
Log in to reply
You might want to look at Karan’s and my further comments, which post-date your comment. It appears that the solution is, at least for the first 40 seconds, quasi-periodic, and does not exhibit odd behaviour. It is also pretty stable under small changes of initial condition. In summary, the behaviour is not that chaotic after all. Euler’s method misses this.
Log in to reply
@Mark Hennings – Yes, very true. Euler's method is quite bad; especially for these oscillating phenomenon. The method is unstable for this problem. The best would be Runge Kutta.
When using numerical methods to solve problems, it is critical to understand that on each time step, an infinitesimal error is introduced. These errors accumulate over time to produce "global errors" that are proportional to the time step in a manner determined by the sophistication of the numerical method. My typical practice is to run the simulation with time steps spanning two or three orders of magnitude, and if the results are approximately the same for all trials, I have confidence in the results. These convergence tests are an indispensable aspect of numerical simulation.
There is another aspect to consider as well, known as "chaos". A chaotic system is one for which slight variation in the inputs or initial conditions has a dramatic effect on the final results. Since the numerical methods introduce errors, these count as deviations in the "initial conditions" for the next loop iteration. Note that chaos can manifest in purely deterministic systems, such as the one under consideration. Another way of summarizing chaos is to say "chaos is when the present determines the future, but the approximate present does not approximately determine the future".
Now, to the problem at hand. To simulate this, I just turned the gravity equations back on from the code from the previous problem. The real interesting thing here is the interpretation of the results under various experimental conditions. There are two experiments of particular interest:
1) Run multiple trials with the same initial conditions but different simulation time steps
2) Run multiple trials with the same simulation time step but slightly different initial conditions
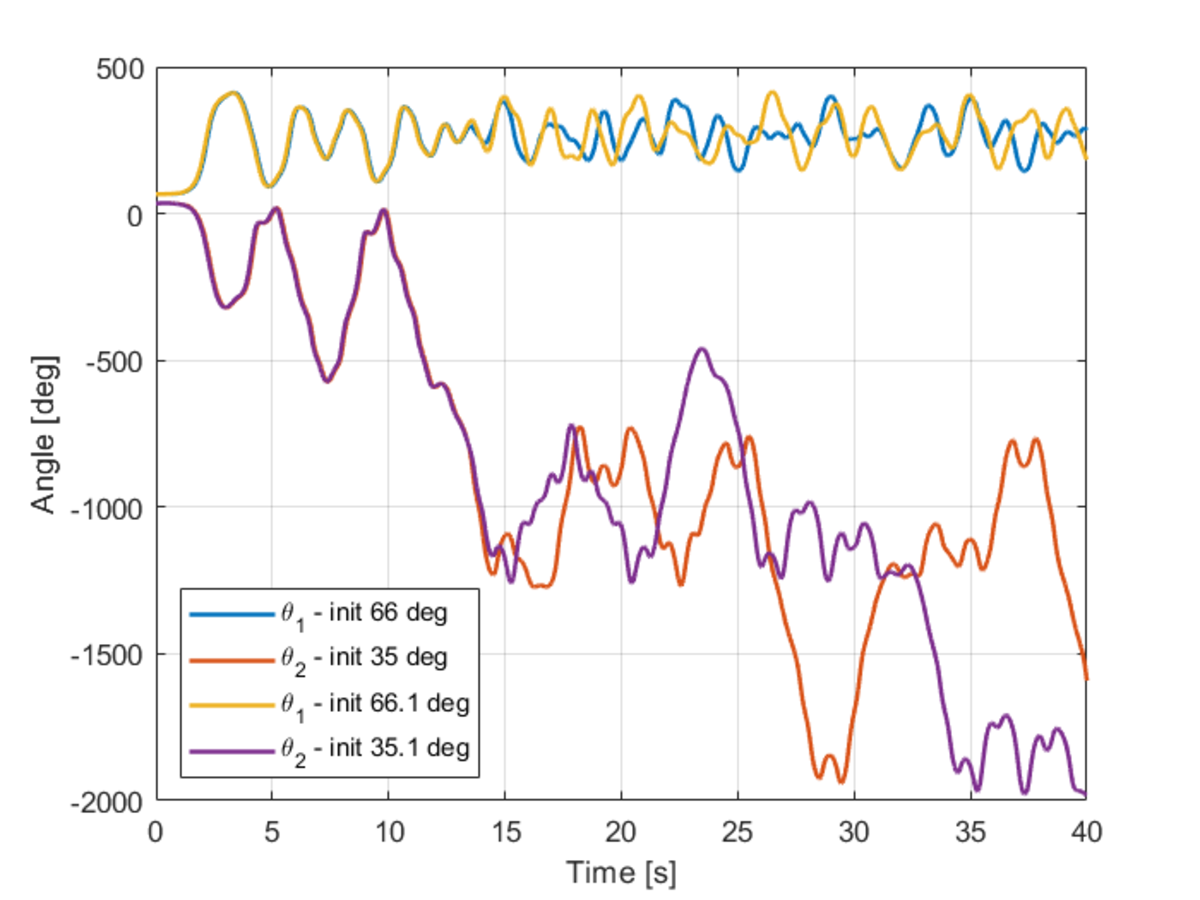
For Case 1, I ran with the given initial conditions, with time steps of ( 1 0 − 4 , 1 0 − 5 , 1 0 − 6 ) . Separate plots are given for θ 1 and θ 2 . It is apparent that all three track with each other for some time, and then radically diverge.
For Case 2, I ran two sub-cases with a time step of ( 1 0 − 6 ) for both, but in one sub-case, θ 1 starts at 6 6 degrees, and in the other sub-case, θ 1 starts at 6 6 . 1 degrees. Again, the two cases yield similar results for some time, and then wildly diverge.
Base on these observations, I think it is fair to say that this system exhibits chaotic behavior. It is well-known that the classic double pendulum exhibits such behavior, so the observations made here are not entirely surprising. Using Lagrangian equations instead of Newtonian equations would likely result in slight differences in the accumulation of numerical errors, which chaos would then seize upon to create large changes in the output.
Simulation Code: