Upward Lifting force on a Cone!
A conical cup of height , semi-vertical angle rests open end down on a flat surface as shown. The cup is filled to height with liquid of density and a small hole is punched at the apex of the cone. The upward lifting force on the cup is , then ' ' is
The answer is 3.00.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
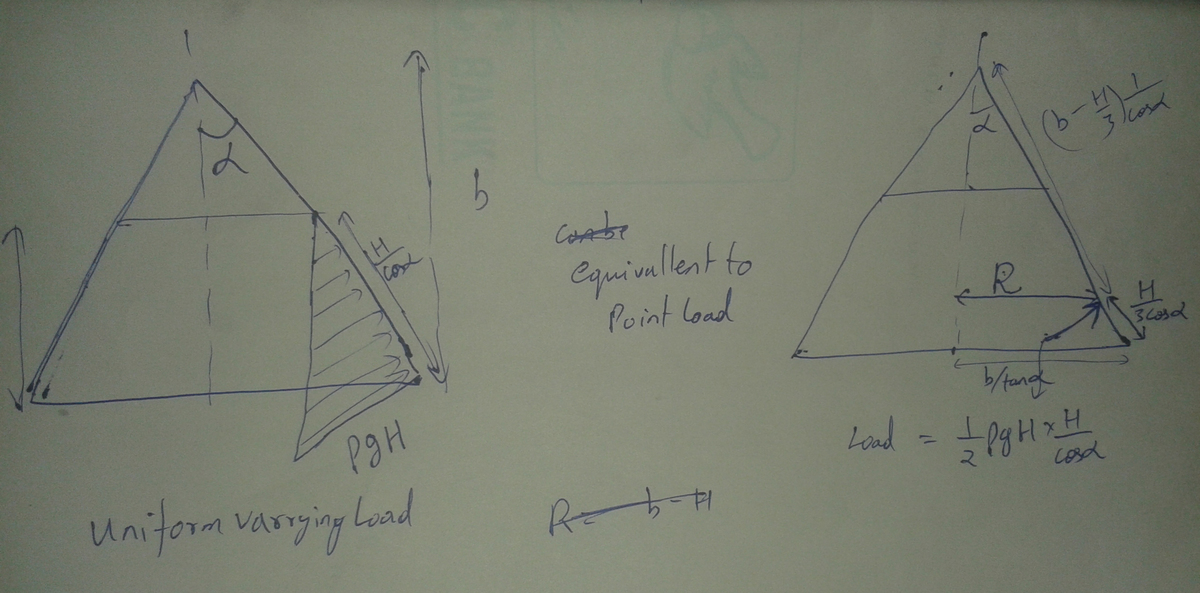
Firstly we have to neglect atmospheric pressure .
Then consider FBD of water .
Forces acting on it are :
net downward force by vertical walls.
Force of gravity
Pressure force exerted By base .
Now , force exerted by walls
F = PA - mg = ( H ρ g ) ( π b 2 t a n 2 α ) − 3 ( π ( b 3 − ( H − b ) 3 ) ( t a n 2 α ) ρ g )