Useful integral #1
∫ 0 2 π ln ( sin ( x ) ) d x
If the value of the integral above equals to − A π ln ( B ) for positive integers A and B , find the value of A B .
Try more here! .
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions

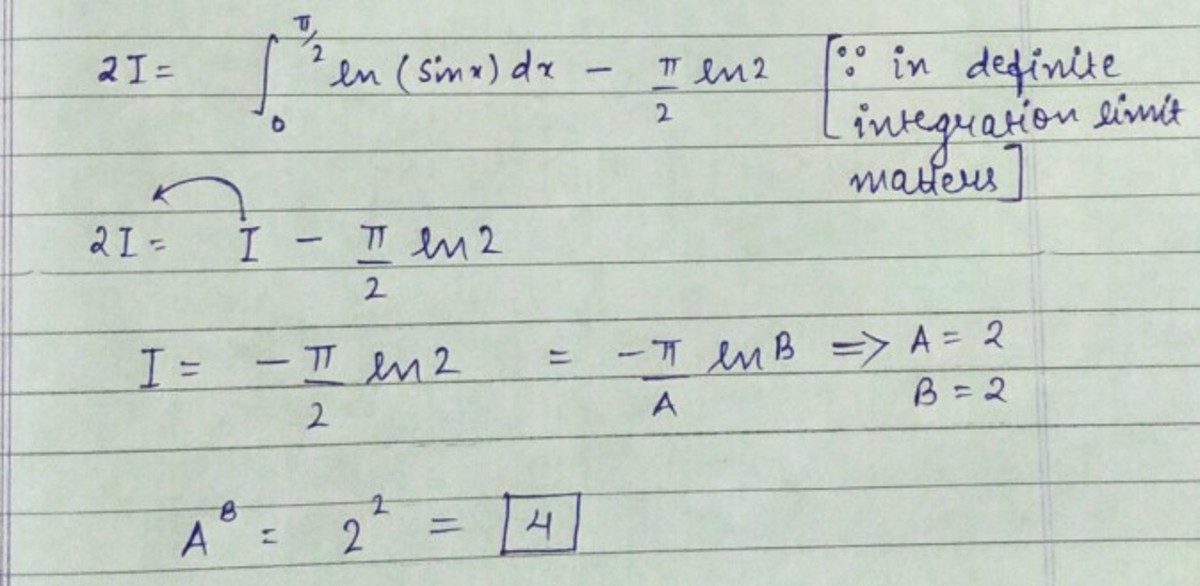
@Raj Rajput You wrote all the limits and properties at side. Thats amazing!!Well i did the same too!
Thanks a lot! The solution was very lengthy, that's why I didn't upload. U saved my time. Thanks a lot. Do try my other problems.
Log in to reply
The question had already been posted .
Log in to reply
Can u provide me a link??
Log in to reply
Log in to reply
@Parth Lohomi – Actually it is a bit different. I can't waste the efforts of Syed and Raj. So just leave it. I know that both lead to the same answer in same methods.
Log in to reply
@Aditya Kumar – in 0 to π /2 ∫ ln ( sin ( x ) ) = ∫ ln ( cos ( x ) ) so there exactly same , but let it be , atleast one can see the difference of sin and cos!
Log in to reply
@Parth Lohomi – Yes that's what I meant to say. I entered the answer in that problem in 2s
Thanks and yes i will try :) :)
Log in to reply
I wouldn't if I were you. Just reading his solution made me pass out.
Log in to reply
@Pi Han Goh – Why what happened?? It uses basics in a complicated manner.
Log in to reply
@Aditya Kumar – Really? I would like to see you evaluate H(1/12) manually.
Log in to reply
@Pi Han Goh – is there something that i have made wrong @Pi Han Goh , i thought solution is perfect :P
Log in to reply
@Raj Rajput – pi han was talking about me. One of my solutions wasn't as expected. There's no problem with your solution.
There is a mistake in your solution,
You have wrote that period of
l
o
g
(
s
i
n
(
x
)
)
is
π
but actually period of
l
o
g
(
s
i
n
(
x
)
)
is 2
π
∫π20ln(sin(x))dx Let's assume the following (eq.1*): I=∫π20ln(sin(x))dx
And we will need this property: ∫a0f(x)dx=∫a0f(a−x)dx
Therefor we can now calculate I: ∫π20ln(sin(π2−x))dx
There is literally a cofunction identity that says: sin(π2−x)=cos(x)
So we can arrive at: ∫π20ln(cos(x))dx
Now by combining eq.1 and the line above, we embark on a long journey: 2I=∫π20( ln(sin(x))+ln(cos(x)) )dx
=∫π20( ln(sin(x)cos(x)) )dx
We will use the following identity: sin(2x)=2sin(x)cos(x)
And get: ∫π20ln(sin(2x)2)dx
Then the log property: ln(AB)=ln(A)−ln(B)
So we get: ∫π20( ln(sin(2x))−ln(2) )dx
Now we split up the equation using simple multiplication: ∫π20ln(sin(2x))dx−∫π20ln(2)dx
We can integrate the right side (ln(2)) first because that is the easiest: ∫π20ln(sin(2x))dx−ln(2)(x)π20
∫π20ln(sin(2x))dx−ln(2)(π2)
Now we are going to use U substitution and should also recognize the symmetry of the sin function about pi/2 (sin(pi/2)=1; think a bell curve): (12)∫π0ln(sin(u))duu=2x−ln(2)(π2)
Note the integral changed, and we can eliminate the .5 that was just added by noticing the following: ∫π0=2∫π20
Thus we can change our integral to: (12)(2)∫π20ln(sin(u))duu=2x−ln(2)(π2)
Since we know from earlier: I=∫π20ln(sin(x))dx
We can say: 2I=I−(π2)ln(2)
Which is reduced to: I=−(π2)ln(2)
Ahah! we have finally arrived at our answer:
∫π20ln(sin(x))dx=−π2ln(2)
∫π20ln(sin(x))dx Let's assume the following (eq.1*): I=∫π20ln(sin(x))dx
And we will need this property: ∫a0f(x)dx=∫a0f(a−x)dx
Therefor we can now calculate I: ∫π20ln(sin(π2−x))dx
There is literally a cofunction identity that says: sin(π2−x)=cos(x)
So we can arrive at: ∫π20ln(cos(x))dx
Now by combining eq.1 and the line above, we embark on a long journey: 2I=∫π20( ln(sin(x))+ln(cos(x)) )dx
=∫π20( ln(sin(x)cos(x)) )dx
We will use the following identity: sin(2x)=2sin(x)cos(x)
And get: ∫π20ln(sin(2x)2)dx
Then the log property: ln(AB)=ln(A)−ln(B)
So we get: ∫π20( ln(sin(2x))−ln(2) )dx
Now we split up the equation using simple multiplication: ∫π20ln(sin(2x))dx−∫π20ln(2)dx
We can integrate the right side (ln(2)) first because that is the easiest: ∫π20ln(sin(2x))dx−ln(2)(x)π20
∫π20ln(sin(2x))dx−ln(2)(π2)
Now we are going to use U substitution and should also recognize the symmetry of the sin function about pi/2 (sin(pi/2)=1; think a bell curve): (12)∫π0ln(sin(u))duu=2x−ln(2)(π2)
Note the integral changed, and we can eliminate the .5 that was just added by noticing the following: ∫π0=2∫π20
Thus we can change our integral to: (12)(2)∫π20ln(sin(u))duu=2x−ln(2)(π2)
Since we know from earlier: I=∫π20ln(sin(x))dx
We can say: 2I=I−(π2)ln(2)
Which is reduced to: I=−(π2)ln(2)
Ahah! we have finally arrived at our answer:
∫π20ln(sin(x))dx=−π2ln(2)
