Vampire fan club?
+ F 3 A F 1 N A 2 G N 2
Each letter represents a different nonzero digit. What is G ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
23 solutions
The second column is indeed 1+A+2, but you have not explained yet at that stage why 1 should have carried over from the third column. Basically, the argument you present a line later on should have been mentioned earlier. All of 1, 2, and 2 cannot be the sum of 2 non-zero and distinct digits, so all the last three columns must carry 1 to the column to their left.
I am new here and this just is not really the best systematic way to achieve the solution for similar problems. I just don't understand why it got the most upvotes.
Log in to reply
There's actually no systemic way - there's a lot of variety to cryptogram solutions, and there are many of these problems which do require a certain amount of logical grinding and don't succumb to a straight algebraic shortcut. I wrote one here that would be the most comprehensible at a basic level (not everyone, especially solving the first problem of the basic set, knows what modular arithmetic is) although I did write the problem with the intent in mind people could find "clever" solutions as well (this means it's a problem that's open to a wide variety of skill levels, and people who were able to solving it by just guessing and checking can learn from others).
I think the upvoting here is purely a function of which solutions people understand the most - since this is the most "elementary" solution it has the most people who can read it.
Log in to reply
Thanks, that explains it. So the simplest looking solutions end up on top.
Don't worry about it. You will be getting used to it. At first when I joined brilliant I too felt that the questions in the easy section are also tough. But after that I got used to it and now I am able to solve many problems. I am also banging a lot of up votes.
Log in to reply
I was not writing about the difficulty of the problem. I meant the non-algebraic nature of the most upvoted solution.
What a bizarre comment.
"this just is not really the best systematic way to achieve the solution for similar problem."
Apparently upvoters don't care about that.
Isn't it supposed to be something like "Since there are only nonzero digits" or "Since all digits are nonzero" in your 2nd sentence?
It’s really dissapointing that your second sentence contradicts the information about nonzero digits. And from a staff member, no less. Your attempt to write concisely and simply was oddly confusing. The users Ram Mohith and x x used equations I’m not familiar with but I was able to fully decipher them and understand some of the ways this problem can be solved. Even though Ive worked through the problem I still can’t understand your explanation because it leaves details out at critical locations and is just bad. I’ve got to say it. It’s bad and I don’t like you. Sorry.
Log in to reply
I think my solution will be clear for beginners. There not much logic in that. From the question you can say that F A N G is a four digit number and F A N . I think you know that any four digit number a b c d can be expressed as 1 0 0 0 a + 1 0 0 b + 1 0 c + d . For example, 1 2 5 6 can be expressed as 1 0 0 0 ( 1 ) + 1 0 0 ( 2 ) + 1 0 ( 5 ) + 6 . And also any three digit number x y z can be expressed as 1 0 0 x + 1 0 y + z . For example, 6 2 5 can be expressed as 1 0 0 ( 6 ) + 1 0 ( 2 ) + 5 . Now the sum of the sum of F A N G and F A N gives us 3 1 2 2 . I just expanded the two numbers and after that I assumed 1 0 0 F + 1 0 A + n as x and founded the greatest multiple of 11 less than or equal to 3 1 2 2 and that's all you have founded the value of G .
Coming to XX's solution it is like a summary of the last part of my solution. But the difference is the solution contains modulus function.
Jason Dyer's solution is completely based on logic. It needs visualization as it is done carry outs of addition.
When you say non-zero. Don’t you actually mean numbers greater than zero? Negative numbers are non-zero
You should make it clearer because the numbers are quite separated from each other, which led me to believe that the numbers were independent and not part of a larger number and there were 4 sums of single-digit integers, not one big sum, so I solved it this way: F = 3, A = -2, N = 4 and G = 6. After all negative numbers are also non-zero.
How do we know that the carried sum is 11? Why not 21, or 31, etc.?
Log in to reply
Well that is at least one part of it that makes sense, because when adding up 2 decimal numbers, the largest carried digit can be just 1. Try adding up numbers like 9999 + 9999 digit after digit manually and see for yourself.
Be careful not to think of the letters as variables; they are digits here. Since we are only adding two rows of digits, the max sum from one column, which is the sum of two digits, would be 18.
If there are no non-zero elements, then all elements must be zero. Your explanation makes zero sense.
This thing makes no sense at al. No value is represented by 0. There is no implication of 1. Unless you specify it. F = 3 is what you have written down.
Your logic of a carry?! Where do your magical number come from??
A + F = 1 A + 3 = 1 A = 1 - 3
Carry what? Carry how? Am I missing something? Can you reference the principles you are using? I’d like to read up on that.
Log in to reply
Before assuming that “it makes no sense,” it might be more helpful to assume that it does make sense but that you might not understand why quite yet.
This is called a cryptogram and there are examples of it in the Mathematics Fundamentals unit.
For this particular problem there are two possibilities in the second column: either A + F = 1 or A + F = 11.
But A + F cannot be equal to 1 (there are no two distinct natural numbers where this could be true).
So, A + F = 11, meaning the one from the tens place in this sum is “carried over” to the next sum in the first column (which is just F). So the 1 that was “carried over” from column 2 to column 1 and F sum to 3. Or, 1 + F = 3, therefore F = 2
Notice the conditions stated in the Problem, letters represent nonzero digits and different digits. So neither A or F can be 0, which alone means A+F=11. You can solve this in multiple ways and I think the one seeing this as 11 FAN + G is the best, but also for looking at the equations of the single result digits you can see this more straight forward from the least significant digit upwards than from the most significant digit backwards.
nice solution
I did this from the least significant digit upwards instead of backwards:
G+N=12 (since no letter can be 0 and both can't be 1, there needs to be a +1 carry over, a result >10. it can't be >20, so it must be 12) =>N+A+1=12 (=> N+A=11) (again can't be >20 and due to the +1 carry a further +1 carry is necessary) =>A+F+1=11 (=> A+F=10) (again can't be >20 and again due to the +1 carry a further +1 carry is necessary) =>F+1=3 =>F=2 =>A=10-F=8 =>N=11-A=3 =>G=12-N=9
This way the solution dripples down from conclusion after conclusion.
I realized that in order for column 1 to equal 3 it would involve a carry. Once I knew that, I just plugged in 9 to prove my theory that there’s more than likely be a carry in each column. I probably did it the hard way, but it worked. Your way makes much more sense.
This original problem should have been under "Intermediate," because of the multiple steps.
Log in to reply
The multiple steps are for better understanding of the community members. Actually you can do these steps in your mind itself.
Log in to reply
Doing multiple steps in my mind does not give validation to keeping this in "Basic."
Log in to reply
@Dennis Rodman – You can consider the second solution, if you like, which is possible to do in your head.
You can even do this solution in your head if you spell everything out a little less rigorously - once you realize the first column has to be a carry, you can do F = 3 and from there think about the second column, then A = 8 and think about the third column, etc.
Note "Basic" doesn't necessarily mean "can be done in your head" although the first two or three of the problem of the week set does tend that way.
F A N G + F A N = G + 1 1 F A N ,so G = 3 1 2 2 ( m o d 1 1 ) = 9 , F A N = 2 8 3
Moderator note:
Note the notation F A N means we are talking about a string of digits.
The first step uses the fact that if you multiply a number by 10, it moves all digits one position to the left, that is:
F A N 0 = F A N × 1 0 which implies F A N G = F A N × 1 0 + G .
This then combines with the second number already written as F A N to make F A N × 1 1 + G .
Can you please clarify this notation? The bar on top? Thanks. And how did you calculate the mod did you use a calculator?
Log in to reply
Bar is a string of digits in this case. If A=1 and B=2, to not confuse with multiplying, A B = 1 2 and B A = 2 1 . For modular arithmatic, you want the remainder, so 3122 divided by 11 is 283.8181, where 0.8181 is 9/11, 9 being the remainder.
This is a very interesting method that skips lots of steps that seemed necessary at first.
here how the 11 came ? can anyone explain ?
This is a nice solution. Esp. since we're only asked for G.
This is the same method that I used.
If asked for, say, N, can the same process be used? In other words, can N be directly calculated using this method? Or do we have to calculate G first and work backwards?
Same solution Good job
Nice approach
Any idea what this notation is exactly called and in what other contexts / scenarios this can be used / applied?
Log in to reply
If you are talking about the line on top of the word F A N , that just means that F , A , and N are digits of a three-digit number. You see that in any problem where the digits of a number are important.
If you are talking about G = 3 1 2 2 ( m o d 1 1 ) , that is modular arithmetic. I recommend checking the Brilliant wiki. You see that in a large range of problems, but especially when the question involves divisibility or remainders.
60 yr brain, just joined up, FAN x 10 + G, I get, mod has different meanings, totally stumped 👎 why 11, incomprehensible solution to basic free question has to be worth learning 🤔
Log in to reply
So you know that F A N G = F A N × 1 0 + G . That means that F A N G + F A N = F A N × 1 0 + G + F A N . That is three numbers being added together. The first number is 10 FANs, the third number is 1 FAN, so they add to become 11 FANs. That is why F A N × 1 0 + G + F A N = F A N × 1 1 + G .
The first part of this sum is a multiple of 11. The second part is a number ( G ) which has to be less than 1 1 . When you divide this sum by 1 1 , you will get the number F A N , and G will be the remainder. Since we know the sum is 3 1 2 2 , then we know that the remainder will be G after we calculate 3 1 2 2 / 1 1 . One way to say this is G = 3 1 2 2 ( m o d 1 1 ) . 3 1 2 2 / 1 1 = 2 8 3 with 9 as a remainder, so F A N = 2 8 3 and G = 9 .
@Andrew Church: F A N + F A N G = F A N + ( F A N × 1 0 + G ) = F A N × 1 1 + G . mod = Modulo; 3122 mod 11 is the remainder of dividing 3122 by 11 (3122 = 283 x 11 + 9, so modulo=9.)
Impressive Solution !
The given condition is :
( F A N G ) + ( F A N ) = 3 1 2 2
⟹ ( 1 0 0 0 F + 1 0 0 A + 1 0 N + G ) + ( 1 0 0 F + 1 0 A + N ) = 3 1 2 2
⟹ 1 1 0 0 F + 1 1 0 A + 1 1 N + G = 3 1 2 2
⟹ 1 1 ( 1 0 0 F + 1 0 A + N ) + G = 3 1 2 2
Let ( 1 0 0 F + 1 0 A + N ) be x
⟹ G = 3 1 2 2 − 1 1 x
Now, we have to find the greatest multiple of 11 which is less than or equal to 3122. Now, 1 1 × 2 8 3 = 3 1 1 3 is the greatest multiple of 11 less than or equal to 3122.
So, G = 3 1 2 2 − 3 1 1 3 = 9
From this we can also find the value of F , A , N . We got that 1 1 × 2 8 3 = 3 1 1 3 ⟹ x = 2 8 3
Now, 1 0 0 F + 1 0 A + N = 2 ( 1 0 0 ) + 8 ( 1 0 ) + 3
⟹ F = 2 , A = 8 , N = 3
If A=4, N=6, G=8, and F = 3,then FANG = 3468 and FAN= 346. Then FANG-FAN= 3468 -346 = 3122 So, G could be 8.
Log in to reply
But the question puts the condition that both the numbers must be added to give 3122 but you should not subtract two numbers to give 3122.
I interpreted the equation as (F x A x N x G) + (F x A x N) = 3122, so then I went (FAN) (G) + (FAN) = 3122 --> Input 6 as G --> (FAN) (6) + FAN = 3122 --> 7FAN = 3122 --> FAN = 446 = 223 x 1 x 2 --> 6 is the only value for G that produces a number for FAN that can be produced through the multiplication of 3 positive non-zero numbers.
I definitely didn't realize this was set up to do vertical addition lol
Log in to reply
The starting step is a mistake you can not write F A N G as F x A x N x G as it is against the rule. You should remember that F,A,N,G are digits and it cannot be expressed as product of four numbers.
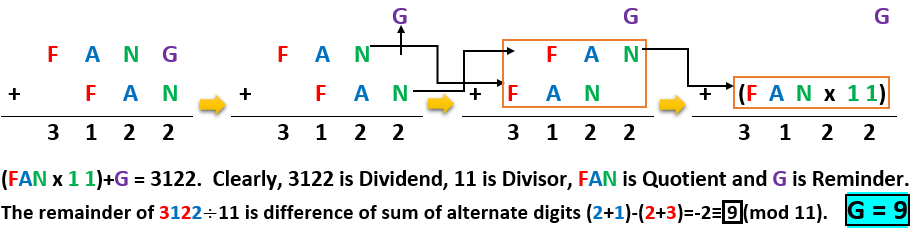 Note:
FAN is multiple of 11. Hence G is the remainder while 3122 divided by 11 which is equal to 9 and FAN is the quotient of 3122 divided by 11 winch is equal to 283.
Note:
FAN is multiple of 11. Hence G is the remainder while 3122 divided by 11 which is equal to 9 and FAN is the quotient of 3122 divided by 11 winch is equal to 283.
The sum is 1 1 F A N + G = 3 1 2 2 . Thus G is the remainder of the division of 3122 by 11. This is equal to ( − 3 ) + 1 − 2 + 2 = − 2 ≡ 9 modulo 1 1 .
FANG+FAN=G+11(FAN) 11(FAN) should be 3113 so G=9
If you consider the sum: FANG + FAN = 3122 as a sum of its parts you see that the sum is equivalent to 1100F + 110A + 11N + G = 3122. The first 3 portions of the sum are all divisible by 11. So, they can be written as 11(100F + 10A + N) + G = 3122. Which means that G must be a single digit number that when subtracted from 3122 produces a multiple of 11. The only number that produces this quality is 9. As 3113 is 11 x 283.
The official answer to the dolphin trying to escape is wrong (July 16, Intermediate problem 1). For some reason, I am not offered the option to add my own solution. Maybe because I supposedly got it wrong. Anyway I am adding it here.
The official answer is that the hole seems higher (That is correct) and that it seems harder to escape because it is smaller (That is incorrect, the apparent hole is actually larger)
This is what happens:
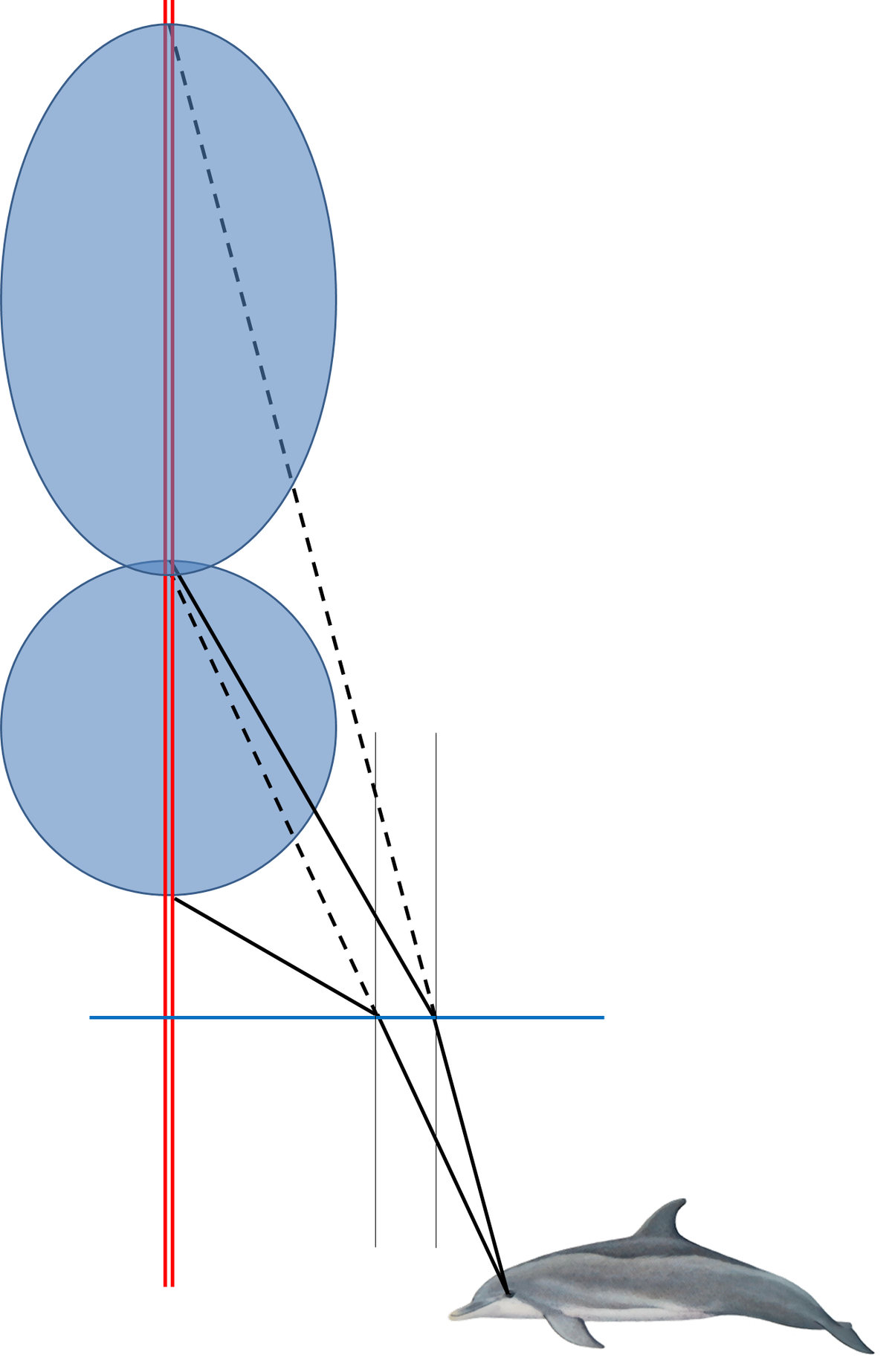
Now lets look more closely at the mathematics of one of the rays.
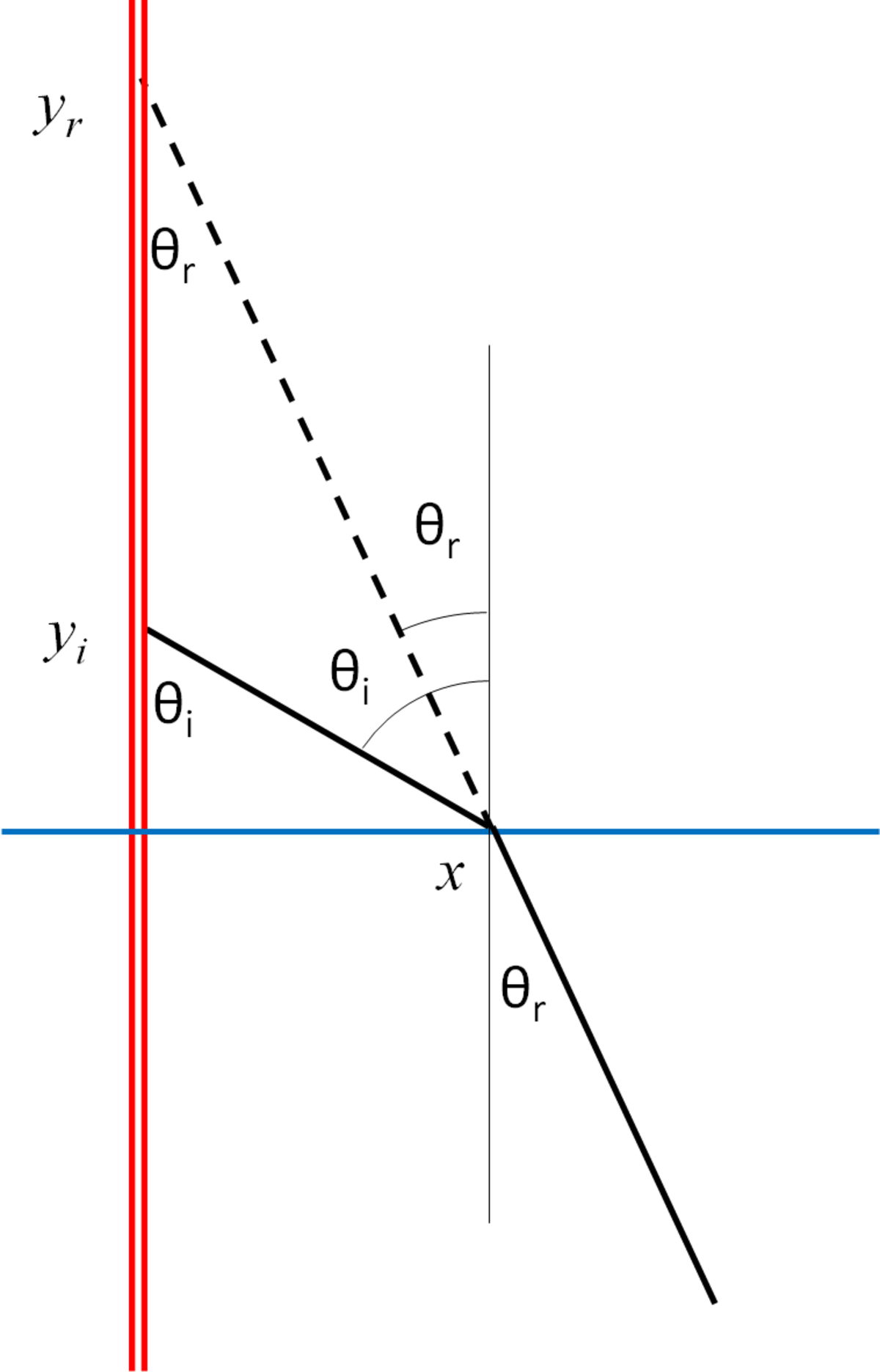
Lets do some maths starting with Snells law of refraction:
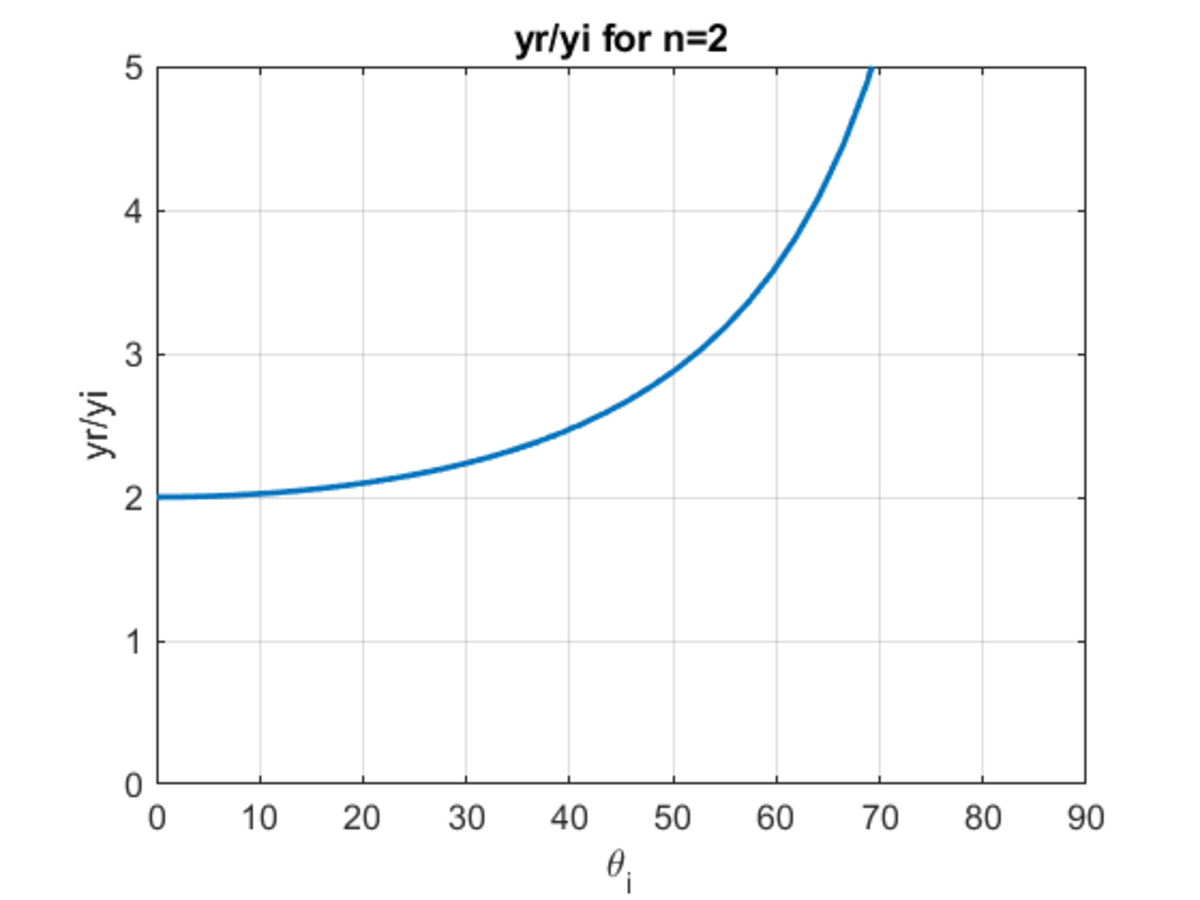
\[ sin θ r sin θ i = v r v i = n i n r = n θ r = sin − 1 ( n sin θ i ) x = y i tan ( θ i ) y r = y i tan ( θ r ) tan ( θ i ) y r = y i cos ( θ i ) n 2 − sin 2 ( θ i ) \)
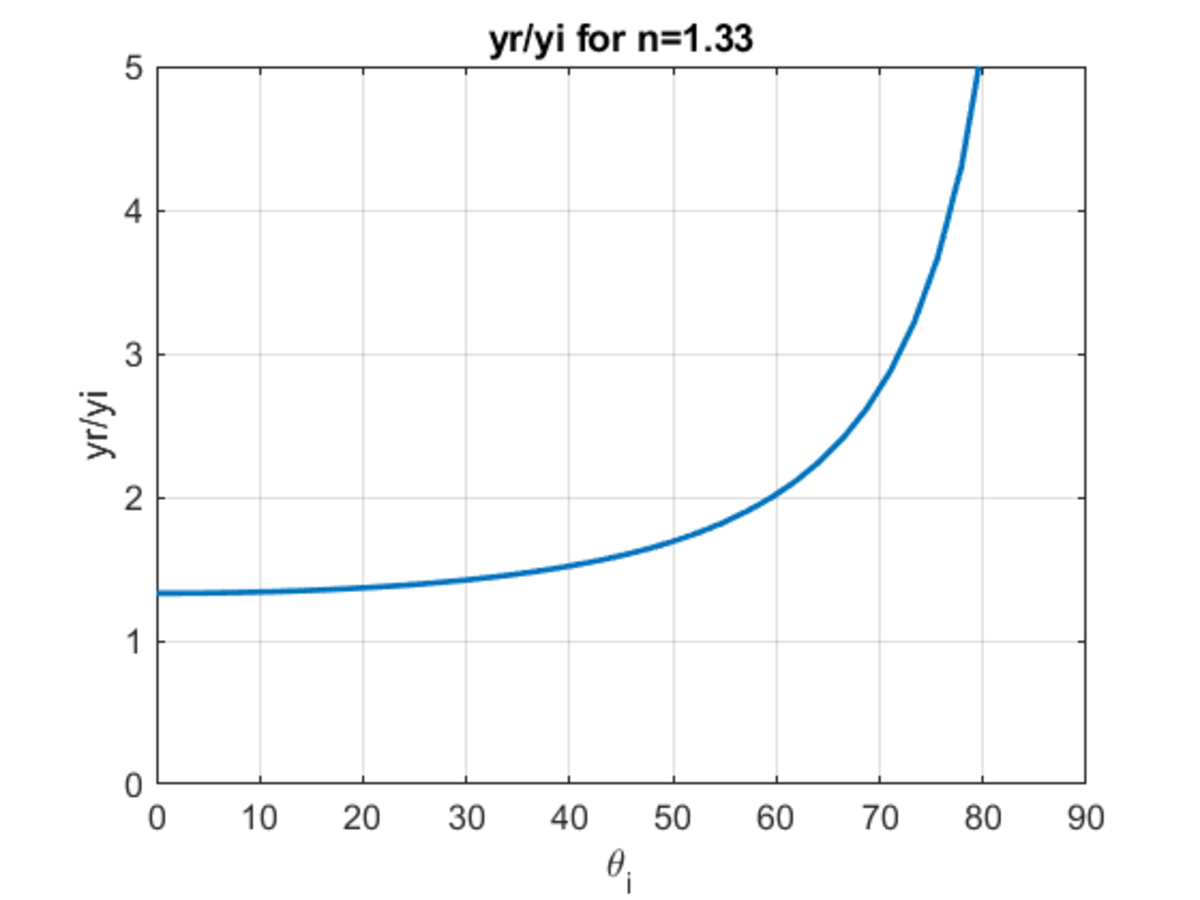
So how does yr/yi change with the angle of incidence?
First with a refractive index of n=1.33:
 Then with n=2.0
Then with n=2.0
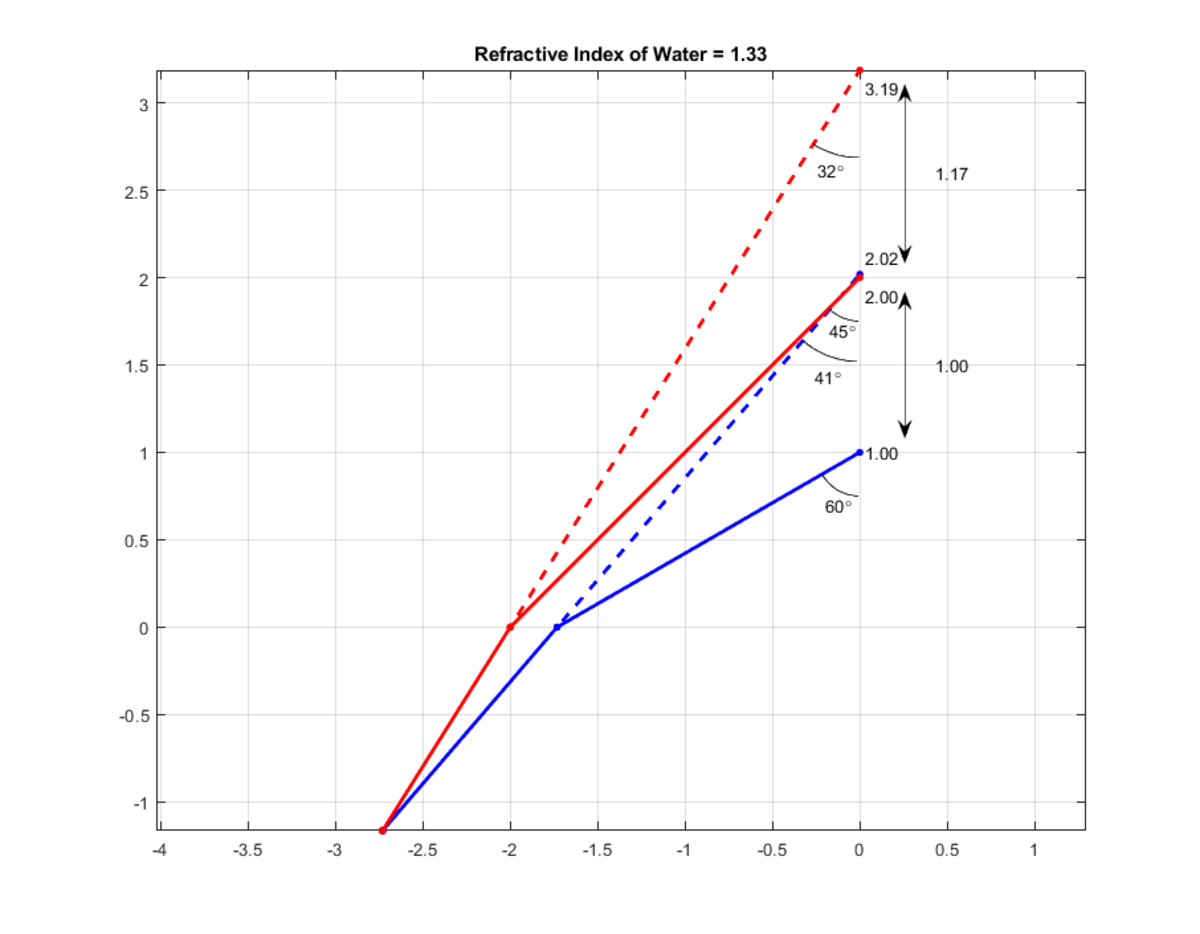
 This show that both edges of the hole get magnified, so the difference will also get magnified.
Here are two examples:
First with n=1.33. The hole edges are at heights of 1 and 2 and angles of incidence of 45 degrees and 60 degrees.
This show that both edges of the hole get magnified, so the difference will also get magnified.
Here are two examples:
First with n=1.33. The hole edges are at heights of 1 and 2 and angles of incidence of 45 degrees and 60 degrees.
 Now the same situation with n=2.0
Now the same situation with n=2.0
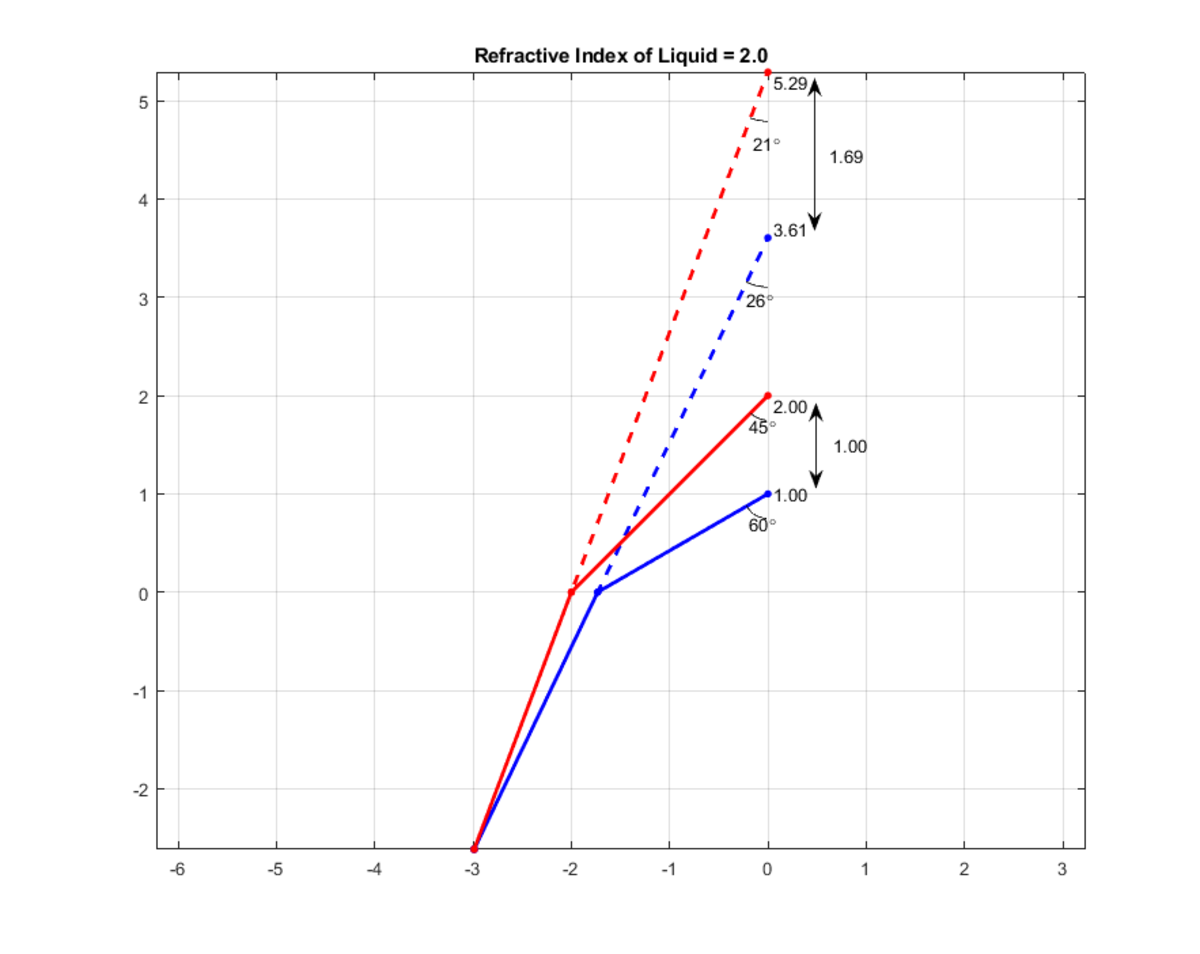
The hole will always appear larger to the dolphin.
I was too lazy to do this on my own, so I wrote some code to do it for me. (Note, it’s not the cleanest code ever, but it works. Written in Swift 4.) ———————————————
import UIKit
let answer : Int = 3122 // the answer
var fang : Int = 2123 // 3122 - 999 var fan : Int = 999 // The highest 3 digit number possible
var fangArray = Array(String(fang)).map{Int(strtoul((String($0)),nil,16))} //converting the FANG integer into an array of digits [2,1,2,3] var fanArray = Array(String(fan)).map{Int(strtoul((String($0)),nil,16))} //converting the FAN integer into an array of digits [9,9,9]
var fangString : String = ("(fangArray[0])(fangArray[1])(fangArray[2])") // pulling the values of the F, A and N digits out of FANG and setting it as a String var fanString : String = String(fan) // setting value of FAN as a string
for _ in stride(from: 101, through: 999, by: 1) {
fang = fang + 1 // Add one to FANG
fan = fan - 1 // Subtract one from FAN
fangArray = Array(String(fang)).map{Int(strtoul((String($0)),nil,16))} // Update FANG array numbers
fanArray = Array(String(fan)).map{Int(strtoul((String($0)),nil,16))} // Update FAN array numbers
fangString = ("\(fangArray[0])\(fangArray[1])\(fangArray[2])") // update FANG string
fanString = String(fan) // update FAN string
if fangString == fanString { // if the digits F-A-N from FANG and F-A-N from FAN match, then print the results.
print("Solution Found!\nThe value of FANG is \(fang),\nthe value of FAN is \(fan).\nThe correct answer is \(fangArray[3])")
break
}
}
————————————————
Copy and paste it into an Xcode playground to see it in action.
Damn, that is crazy, well done, and btw great programming skills man :)
Wolfram alpha system: G+N=a10+2 , N+A = b10+2-a , A+F=c10+1-b , F = 3-c, (a = 0 || a = 1) && (b = 0 || b = 1) && (c = 0 || c =1)
generic solution by https://norsigma.com
FANG + FAN = 10 FAN + G + FAN = 11 FAN + G. (FANG + FAN) mod 11 = 3122 mod 11 = 9, therefore (11*FAN + G) mod 11 = G mod 11 is also 9. Since G is a positive digit, G = 9.
+ F 3 A F 1 N A 2 G N 2 Note that the thousands digit is greater than the hundreds digit. Because F appears in both columns, the hundreds sum must have carried over a 1, by the fact that all the variables are all digits 1 to 9. Therefore, F = 3 − 1 = 2 . + 2 3 A 2 1 N A 2 G N 2 This next part is a little tricky. It could be that N + A > 1 0 , and we could easily assume A = 9 without thinking about it. To err on the side of caution, let's not touch any of the variables and instead simplify this formula, using the fact that the hundreds sum resolves as greater than 10: + A 9 N A 2 G N 2 The tens column is now less than the hundreds column. Therefore, A = 9 − 1 = 8 . + 8 9 N 8 2 G N 2 And again: + N 4 G N 2 The ones column is now less than the tens column. Therefore, N = 4 − 1 = 3 . + 3 4 G 3 2 Now we just simplify again to get our answer: G = ( 4 2 − 3 3 ) = ( 1 2 − 3 ) = 9
Observing the leftmost place ; F can be either 3 or 2 ( F = 2 when there is a carry from previous stage) . A + F = 11 (as F is 2 or 3) ; so its evident that a carry has been sent to leftmost place . Hence F= 2. A + F =11 ; so A can be 9 or 8 ( A = 8 when there is carry from previous stage; which holds as N + A should be 12 as A = 8 or 9. Therefore A = 8; N should be 4 or 3 as A + N = 12; G + N should be 12 as N can take vales either 4 or 3 only ; there is a carry from previous place so N =3 ; hence G =9.
I answered this question yesterday 7/16/18 to continue my streak..this morning it shows as unanswered again...so I did it again..and did third in easy set..still did not take it..streak should be 112 days not one...what is the matter with app
Since G can equal only one of the following: 5,6,7,8, or 9, you can work it out by the exhaustion method, and you finally get the following: G=9, N=3, A=8, and F=2.
It wasn't too exhausting because I started with the 9. It just seemed easier to me to do the carrying in the usual direction rather than work from the front.
G + N = 2 or 12
N + A = 2 or 11 (because if G + N = 12, we would carry over a 1 so 11 + 1 would give us the "2" in the tens spot)
A + F = 1 or 10 (same reasoning as above)
So F must equal 2 or 3 - let's see which one it is.
>
Let F = 2
A = 8 since A + F = 10 (because A + F cannot equal 1)
N = 3 since N + A = 11(because N + A cannot equal 2)
G = 9 since G + N = 12 (because G + N cannot equal 2)
Test: 2839 + 283 = 3122, it works!
>
Let F = 3
A = 7 (same reasoning as above)
N = 4 (same reasoning as above)
G = 8 (same reasoning as above)
Test 3748 + 374 = 4122, which is too much so this is not correct.
>
Thus, G = 9 is the answer.
I did the same
Though this is an algebra question, humour me We can first identify that for this particular problem we are working with non-zero digits, as such let us consider how we can arrive at 2 from the first column. We can have either 1+1 or some sum to 12, which cannot be the same digit twice; not 6+6. So the combinations we can use are: 7+5, 8+4, 9+3. Intuitively, we realise for the first two columns, the solution will have the same value with different digits because of the extra 1 from the carry, To arrive at 3 for the result from the final column we must realise that since one of the digits reduces by one, and the other is conserved, the puzzle must begin with the largest combination, (9+3). Please poke as many holes and point out as many things as possible in this solution :)
divide 3122 by 11. G is remainder
Since each letter represents a unique digit
FANG
FAN
---------------
3122
G+N = 12 A+N = 11 A+F = 10 F = 2
Hence A = 8; N = 3 and so G = 9
Verifying the addition
2839 + 283 = 3122
I did this using the guess and check method or the trial and error method. Since the sum of F A N G and F A N is a four digit number, G + N = 1 2 . So G + N can be
3 + 9 , 4 + 8 , 5 + 7 , 7 + 5 , 8 + 4 , or 9 + 3
Now if you start from 3 + 9 = 1 2 and observed the result, you can try 9 + 3 immediately.
1 2 3 4 5 6 7 |
|
1 |
|
I did it by trying all the numbers: solve: "Each letter represents a different nonzero digit"
G+N= 12 if
G = 9,8,7,5,4,3 according to above: G ≠ 0,1,2,6
N = 3,4,5,7,8,9 according to above: N ≠ 0,1,2,6
N+A= 11 if
N=9,8,7,5,4,3 according to above: N≠0,1,2,6,
A= 2,3,4,6,7,8 according to above: A≠0,1,5,9
A+F= 10 if
A=2,3,4,6,7,8 according to above: A≠0,1,5,9
F=8,7,6,4,3,2 according to above: F≠9,5,1
F+1= 3 if
F= 2 we must now use all the information we have learned!!
f=2 A=8
A=8 N=3
N=3 G=9
Can you believe it took me 45 minutes to write this
luckily it's over now
Assume G to be 9:
Then must N = 3 Then must A = 8 Then must F = 2
Just one answer can be true. Therefore 9 is the correct solution.
Consider the second column written as A + F = 1 . Since there are no nonzero digits, this must involve a carry; that is, the actual sum must be 11. Therefore the first column has a 1 carried from the second column.
This implies 1 + F = 3 , so F = 2 .
+ 2 3 A 2 1 N A 2 G N 2
N and A are different in the third column, and no digits are zero, so the sum in this column must be 12; this means there will be a 1 carrying into the second column. The second column is 1 + A + 2 = 1 1 , so A = 8 .
+ 2 3 8 2 1 N 8 2 G N 2
By the same argument as with N and A in the third column, with N and G in the fourth column there will be a 1 carrying into the third column.
So from the third column, 1 + N + 8 = 1 2 . This means N = 3 .
+ 2 3 8 2 1 3 8 2 G 3 2
The fourth column is then G + 3 = 1 2 , so G = 9 .