Variable density - SHM
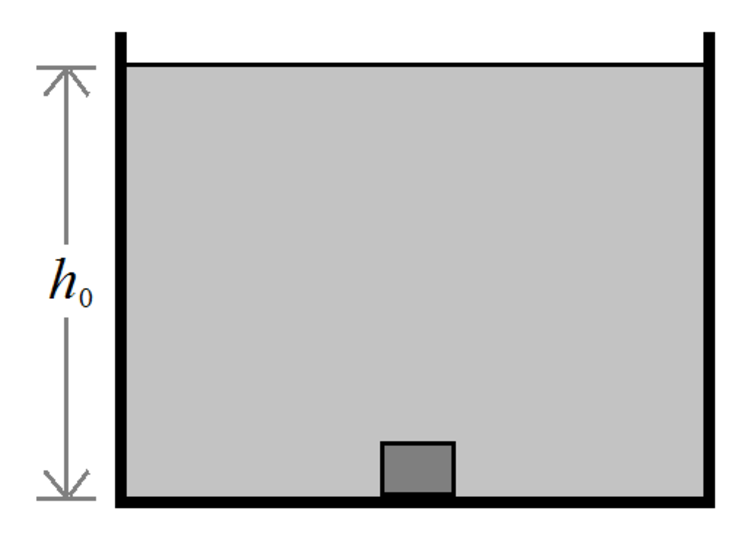 A tank contains a special liquid of depth
h
0
. The density of the liquid varies with
h
measured from the bottom of the tank as
A tank contains a special liquid of depth
h
0
. The density of the liquid varies with
h
measured from the bottom of the tank as
ρ = ρ 0 ( 4 − h 0 3 h )
where ρ 0 is a constant with appropriate demensions.
A small solid block of density 2 . 5 ρ 0 and mass m is released from the bottom of the tank. If the block oscillates with a frequency of α h 0 g , where g is the acceleration due to gravity, find α .
The answer is 0.174.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Karan Chatrath Thanks for the solution. Did you have attempted thermo problems? and from where your are revising thermodynamics?
Log in to reply
I attempted them and I got my initial tries wrong. I have not got time to revise, but I think I might look back at my old copy of HC Verma, when I do.
Log in to reply
@Karan Chatrath HC verma is good, but not that much. Try some more advanced books. They will directly help you in these problems.
Log in to reply
@Talulah Riley – Okay, which one do you suggest?
Log in to reply
@Karan Chatrath
–
@Karan Chatrath
( DC Pandey Waves and Thermodynamics )or( Physics Galaxy Waves and Thermodynamics)
2nd book is more advanced.
@Karan Chatrath Do you have knowledge of solving electrical circuits using phasor diagram?
Log in to reply
I prefer using complex numbers instead of phasor diagrams.
@Karan Chatrath something like that lagging ?
@Karan Chatrath I have a very small doubt in one question, can you help me now?
Log in to reply
Okay, I will try
Log in to reply
@Karan Chatrath
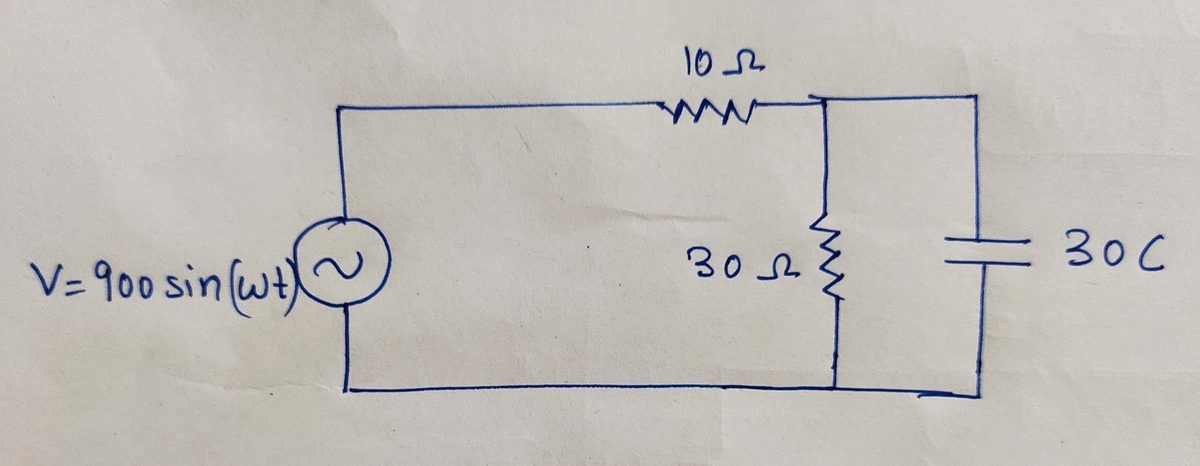
Find the net impedance, power factor of this circuit
@Karan Chatrath which is more easy complex or phasor?
Log in to reply
complex is easier according to me.
In the problem that you shared, the magnitude of net impedance I found is:
Z M = ( 9 0 0 ω ) 2 + 1 ( 9 0 0 0 ω ) 2 + 1 6 0 0
Log in to reply
@Karan Chatrath The answer given behind my book is in terms of phasor, now how I can convert your answer in phasor?
Log in to reply
@Talulah Riley – Well, using complex numbers and phasors are equivalent. And there is more than one notation for a phasor. So show me the form of the answer.
Log in to reply
@Karan Chatrath – @Karan Chatrath modulus of impedance is 8 5 0
Log in to reply
@Talulah Riley – In the diagram, you did not mention frequency. So my answer is in terms of frequency.
Log in to reply
@Karan Chatrath – @Karan Chatrath what type of frequency you are talking about?
Log in to reply
@Talulah Riley – Frequency of the source. You wrote V S = 9 0 0 sin ( ω t ) . What is ω ? The capacitance is 30F if I am right and the resistances are 10 and 30 ohms.
Log in to reply
@Karan Chatrath – @Karan Chatrath no value of ω is given.
Log in to reply
@Talulah Riley – Then I do not know how to solve the problem. The capacitive reactance is
X C = ω C − j
Without ω , I cannot calculate the impedance of the circuit. Does the problem ask for the maximum or minimum impedance over the range of all frequencies?
Log in to reply
@Karan Chatrath
–
@Karan Chatrath
Yes , asking about maximum.
I am also bit confused.
Can you check and your answer and please tell me if it is coming
8
5
0
?
@Karan Chatrath
The problem is resolved. It was just a nonsense of my friend. Leave it.
Now show me the method of your complex number.
And treat it as a new problem. Forget everything about past.
Log in to reply
I have posted a problem on this circuit. You may try it. Hopefully, someone else will share a solution, through which you can gain some insights.
Log in to reply
@Karan Chatrath Thank you so much.
Log in to reply
@Talulah Riley – There is a very fast way to solve this problem, without any tedious calculations. Think about it.
@Karan Chatrath Are you the solver of my latest thermo problem?
The equilibrium is established when
2 . 5 ρ 0 2 5 ⟹ h = ρ 0 ( 4 − h 0 3 h ) = 4 − h 0 3 h = 2 h 0
When the block overshot h = 2 h 0 by x , the density of the liquid the block displaced is
ρ = ρ 0 ( 4 − h 0 3 ( x + 2 h 0 ) ) = 2 . 5 ρ 0 − h 0 3 ρ 0 x
This means that there is an restoring force of h 0 3 ρ 0 V g x , where V is the volume of the block. This must be equal to the m x ¨ , where x ¨ is acceleration of the block. Then we have:
m x ¨ + h 0 3 ρ 0 V g x 2 . 5 ρ 0 V x ¨ + h 0 3 ρ 0 V g x x ¨ + 5 h 0 6 g x = 0 = 0 = 0 Note that m = 2 . 5 ρ 0 V
The frequency of oscillation is then f = 2 π 1 5 h 0 6 g . Therefore α = 2 π 1 5 6 ≈ 0 . 1 7 4 .
Consider a cuboidal element of fluid of height δ y and cross section area δ A at a height y above the bottom of the container. By drawing a free body diagram, one can balance all forces along the vertical direction. Let the pressure on the lower face of this element be P and that on the upper surface be P + d y d P δ y .
The force balance looks as such:
P δ A = ( P + d y d P δ y ) δ A + ρ δ y δ A g ⟹ d y d P = − ρ g
Now, consider the mass to be at a distance y above the bottom of the container. Then, by applying Newton's second law to this small mass gives the following. Consider the mass to have a cross section area of δ A m and length of δ y m .
P ( δ A m ) − ( P + d y d P ( δ y m ) ) ( δ A m ) − m g = m y ¨ ⟹ − d y d P ( δ y m ) ( δ A m ) − m g = m y ¨
m = 2 5 ρ o ( δ y m ) ( δ A m )
Substituting all expressions and simplifying gives:
( 4 − h o 3 y ) g − 2 5 g = 2 5 y ¨
This equation represents an oscillatory motion of frequency:
ω 2 = 5 h o 6 g