Can You Resist The Donut?
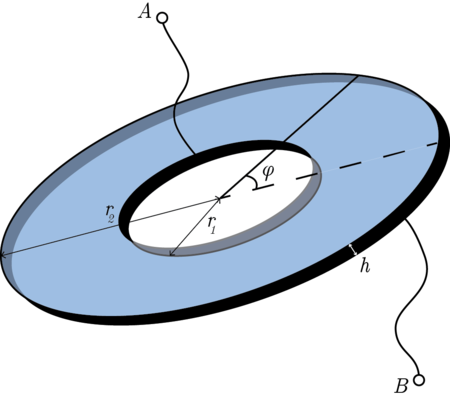
You are given a disk of thickness h with inner and outer radii r 1 and r 2 , respectively. If the resistivity of the disk varies as ρ = ρ 0 ∣ sec φ ∣ , where φ is the polar angle, find the resistance between the points A and B .
Give your answer to 3 decimal places.
Details and Assumptions:
- The inner and outer rims are metal rings with zero resistance.
- Take r 1 r 2 = e 2 ≈ 7 . 3 8 9 , ρ 0 = 1 0 Ω m , and h = 3 c m .
The answer is 166.667.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Same method , Just one difference that I 1st integrated for parallel and then series .
Nice Question :)
Log in to reply
Thanks Aniket!
Log in to reply
see my original problem too : here
Log in to reply
@A Former Brilliant Member – I am getting an answer... t = 6 3 7 9 . 2 4 s
Beautiful question and a equally good solution, and coincidentally, all my steps (including the diagram) while solving it were the same as that of your solution! I would be even happier if this question is an original innovation of yours
Log in to reply
Thank you. By the way, it is! (Except the name :) )
Log in to reply
You mean the question is original, but the name isn't?!
Log in to reply
@Swagat Panda – Yeah. Somebody else renamed this question! I liked the name so much!
Log in to reply
@Kishore S. Shenoy – I have to agree that the name is quite interesting and attractive.
why it happens with me only ? put the answer there as 166.6 but, no, it refused at one point i was thinking to press the discuss solution button but as it happened with me in aniket's problem i decided to close my eyes and put 166.66666666666667 and whoa, got it correct !
Log in to reply
Only 8% tolerance I guess. Report it. They'll find a solution...
hey bro @Kishore S Shenoy how do you draw these great pics ? ( which software ?)
@Kishore S Shenoy , I am also a FIITJEE SOUTH DELHI student for JEE ADV 2018. Can you please suggest some books on physics which can help me to solve calculus based problems? Like to find tension in an elemental part of rope, problems to find electric flux and all that.
Log in to reply
Irodov is a fine book. Use solutions too. Solutions can be found here .
The inner and outer rings are equipotentials, and ∇ 2 Φ = 0 , and hence we have Φ = α + β ln r for some constants α , β . Thus the potential difference is V = Δ Φ = β ln r 1 r 2 .
The current density is j = ρ − 1 E = ρ − 1 ∇ Φ = ρ 0 ∣ cos ϕ ∣ d r d Φ r ^ = ρ o r β ∣ cos ϕ ∣ r ^ and so the current flowing in the circuit is I = ∫ 0 2 π ρ 0 r β ∣ cos ϕ ∣ r h d ϕ = ρ 0 4 β h so that the resistance of the annulus is I V = 4 h ρ 0 ln r 1 r 2 = 4 × 0 . 0 3 1 0 × 2 = 1 6 6 . 6 6 7 Ω
Where did you used to write these? Do you have an iPad?
I just wrote it by hand on paper and then scanned it. But that was back in my pre-latex days
O i see... Nice... Your handwriting seems far better than me

Let's take a small volume as shown.
Since in that sector, infinitesimally small resistors are connected in series, d R = d S ρ d r
where d S is the cross sectional area. d S = r d φ ⋅ h , so the value becomes d R = r h d φ ρ d r R = h ρ ∫ r 1 r 2 r 1 d r = h d φ ρ ln ( r 1 r 2 )
Now, we see that there are infinitesimally small sectors arranged parallely. Using R 1 = ∑ R i 1 = ∫ R ( x ) 1 d x , we get,
d ( R 1 ) = ρ ln ( r 1 r 2 ) h d φ R 1 = ρ 0 ln ( r 1 r 2 ) h ∫ 0 2 π ∣ sec φ ∣ 1 d φ = ρ 0 ln ( r 1 r 2 ) 4 h ⇒ R = 4 h ρ 0 ln ( r 1 r 2 )
Substituting values, we get R = 3 5 0 0 Ω