Dancing wire

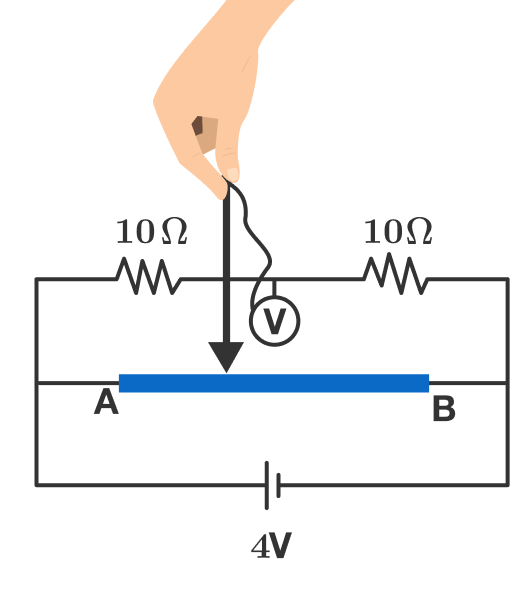
In the circuit above, wire $AB$ has length $40\text{ cm}$ and resistance per unit length $\SI[per-mode=symbol]{0.5}{\ohm\per\centi\meter}$ . The voltmeter is ideal.

If we want to make the reading in the voltmeter vary with time as $V(t) = 2 \sin(\pi t) \ \si{\volt},$ then what should be the velocity of the contact (the arrow-tipped end of the wire above) as a function of time?

If the velocity can be expressed as $A\sin(\omega t+\phi) \text{ cm}\,\text{s}^{-1},$ where $0<\phi<\pi$ , then enter the value of $\dfrac A{\omega- \phi}$ .