Vieta's Derivative II -- My 500-follower problem
The function
x
5
+
6
x
4
−
1
8
x
3
−
1
0
x
2
+
4
5
x
−
2
4
has only four distinct real roots:
α
,
β
,
γ
and
δ
(in no particular order). If
f
′
(
x
)
is the first derivative of
f
(
x
)
. Evaluate
f ′ ( α ) + f ′ ( β ) + f ′ ( γ ) + f ′ ( δ )
Inspiration: This is exactly the problem titled Inspired by Vieta's Derivatives with a twist.
The answer is 4797.000.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Thanks for the answer. It helps if you plot a graph. We can do it quite fast using a spreadsheet.
Log in to reply
My favorite part of the problem is the clause "with a twist": it is quite literally a twist, as the × sign has been rotated 4 5 ∘ .
Thanks! I only use them as a last resort or if I'm feeling lazy.
Log in to reply
I understand. You like to exercise your brain first. But for me I make quite a bit or careless mistakes, therefore, need to use a surer way.
Log in to reply
@Chew-Seong Cheong – To each his own! Big fan of your answers!
is there any easy way to do it ....?
Log in to reply
I doubt there is one. One slightly simpler way to factor out ( x 2 − 3 ) after ( x − 1 ) 2 has been factored out is to consider the equation x 3 − 3 x = 8 x 2 − 2 4 ⇒ x ( x 2 − 3 ) = − 8 ( x 2 − 3 ) . But this only simplify the overall working by a little.
Log in to reply
i did the same and got wrong due to calculation mistakes!!
these type of question gets us tired and tedious ....!!
but still a good question indeed!
good question but far too tedious.............
This is in response to Aman Gautam 's comments. I hope this is helpful.
I find it easy to solved it using an Excel spreadsheet. Which I am going to show here.
First we can plot the graph of f ( x ) = x 5 + 6 x 4 − 1 8 x 3 − 1 0 x 2 + 4 5 x − 2 4 . From the calculated data, we see that there are four real roots − 8 , ( − 1 . 7 5 , − 1 . 5 ) , 1 , ( 1 . 7 5 , 1 . 5 ) .
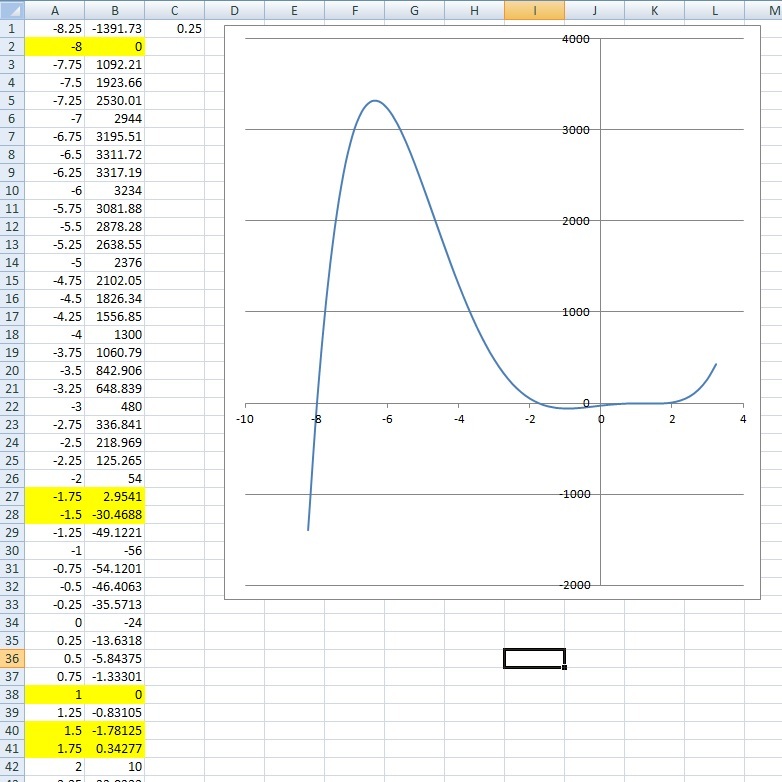
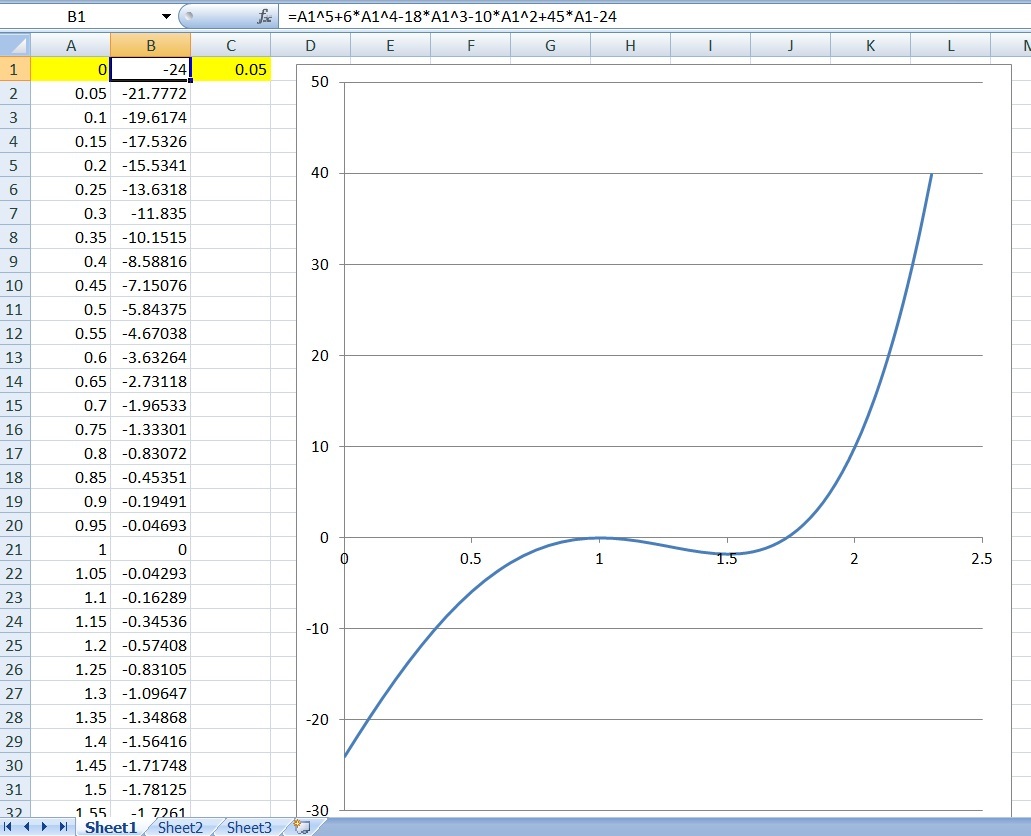
By changing the starting
x
value (Cell A1) and the graph scaling (Cell C1), we can zoom in around
x
=
1
we see that
x
=
1
is the double root (see below). We can confirm this by putting values in
f
′
(
x
)
=
5
x
4
+
2
4
x
3
−
5
4
x
2
−
2
0
x
+
4
5
. (Notice the formula in Cell B1.)
Then we can use spreadsheet to do long division by the known factors x − 1 , x − 1 , x − 8 , as follows:
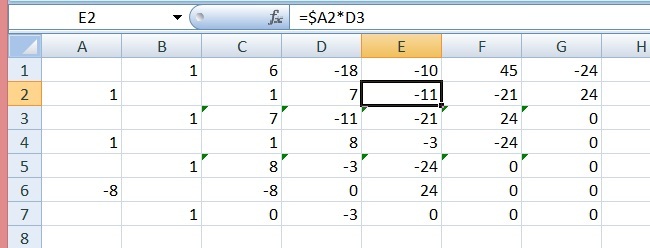
Row 1 is the coefficients of f ( x ) . Column A is the factors. Row 3 is the quotient of x − 1 f ( x ) ⇒ f ( x ) = ( x − 1 ) ( x 4 + 7 x 3 − 1 1 x 2 − 2 1 x + 2 4 ) .
Similarly, Row 5: ⇒ f ( x ) = ( x − 1 ) 2 ( x 3 + 8 x 2 − 3 x − 2 4 )
And, Row 7: ⇒ f ( x ) = ( x − 1 ) 2 ( x + 8 ) ( x 2 − 3 )
Therefore, the remaining two roots are ± 3
Of course, we can use the speadsheet to calculate the value of f ′ ( α ) + f ′ ( β ) + f ′ ( γ ) + f ′ ( δ ) .
just Brilliant!
By Rational Root Theorem and the suggestion of the description, by perform long division twice, we can see that x = 1 is double root of the equation. Therefore leaving the cubic polynomial ( x 3 + 8 x 2 − 3 x − 2 4 ) .
A few tedious trial and error for factors of ± 2 4 gives x = − 8 as another root for the cubic polynomial. So the equation factors completely to ( x − 1 ) 2 ( x + 8 ) ( x 2 − 3 ) . Thus the value of the expression in question is simply f ′ ( 1 ) + f ′ ( − 8 ) + f ′ ( 3 ) + f ′ ( − 3 ) .
With f ′ ( x ) = 5 x 4 + 2 4 x 3 − 5 4 x 2 − 2 0 x + 4 5 , we can easily obtain f ′ ( 1 ) = 0 and with enough patience, we get f ′ ( − 8 ) = 4 9 4 1
And f ′ ( x ) + f ′ ( − x ) = 2 ( 5 x 4 − 5 4 x 2 + 4 5 ) , with x = 3 , we have f ′ ( 3 ) + f ′ ( − 3 ) = 2 ( 5 ⋅ 3 2 − 5 4 ⋅ 3 + 4 5 ) = − 1 4 4
The answer is 0 + 4 9 4 1 − 1 4 4 = 4 7 9 7