Vikram's Circles
An infinity of circles covers part of the plane in a fractal spiral. As the figure below shows, there is one largest circle, which we'll call the first one, followed by others whose radii are in geometric progression. The 9 th and 1 0 th circles are tangential to the first circle.
Let A be the total area of all the circles, and B the total area of the interstitial spaces formed by these circles. What is ⌊ 1 0 0 0 × A + B A ⌋ ?
Bonus Question: Does "circle area density on the infinite plane" always has a meaning? For a regular array of circles on the infinite plane, it does. When does it fail to have a meaning? Consider the case of "mass density" of the universe, for example. Does that always necessarily have a meaning?
The answer is 953.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Yes, the "cycle" of 8 circles is arbitrary. Or is it 9? This problem was once proposed by Vikram Pandya quite a while back, why he chose 8, I don't recall. Besides the main obvious spiral, each circle is part of 2 other spirals. I was going to think up a problem based on that. The plane can be tessellated into curved triangles similar to either one of 2 types.
Very nice solution! I liked your complex analysis approach.
The fractal nature of the pattern is obtained provided that the 0 th, 8 th and 9 th circles are mutually tangent, which means that we require ∣ 1 − z 8 ∣ = ρ ( 1 + ∣ z ∣ 8 ) ∣ 1 − z 9 ∣ = ρ ( 1 + ∣ z ∣ 9 ) Solving these equations numerically, the only physically reasonable solution (for z with positive argument) occurs when z = r e i θ with r = 0 . 9 2 6 5 5 5 and θ = 0 . 7 3 1 6 0 2 .
Sorry, I don't follow. How do you solve these equations numerically? I can't seem to isolate the equation in terms of one of r or θ .
What I did was: Set ρ as the subject from both these equations. And ∣ z ∣ 8 = r 8 , ∣ z ∣ 9 = r 9 . But the expression for ∣ 1 − z 8 ∣ and ∣ 1 − z 9 ∣ are not so simple to tackle. ∣ 1 − z 9 ∣ = r 1 8 cos 2 ( 9 θ ) + sin 2 ( 9 θ ) . I'm stuck now. (sigh)
I believed I'm missing something fundamental here...
Log in to reply
The two conditions can be written as a pair of (highly nonlinear) simultaneous equations for the modulus r and argument θ of z , since ∣ 1 − z n ∣ = 1 + r 2 n − 2 r n cos n θ
We know that r < 1 , but r ≈ 1 , and that θ < 4 1 π , with θ ≈ 4 1 π .
There are many methods for solving simultaneous equations numerically. A simple one is a multidimensional version of Newton-Raphson - see here . This method is not perfect, and so the NR method has to be shored up to make it more reliable.
I must admit that I am not hugely interested in the nitty-gritty of numerical calculation - I leave it to those who are - and so Mathematica's NSovle and FindInstance are my favourite methods!
Log in to reply
Ah, thanks. I thought you managed to isolate one of these variables. I was wondering how you seemingly pulled it off so effortlessly.
There are many methods for solving simultaneous equations numerically. A simple one is a multidimensional version of Newton-Raphson - see here .
Many? I must be living under a rock. I thought NR is the only way? What other amazing methods do you know?
Log in to reply
@Pi Han Goh – The Broyden paper represents a class of techniques. NR does not always pick the right direction, and sometimes only works if the initial guess is close to the answer, and that paper discusses a number of ways of being more reliable. There are other add-on algorithms which sharpen the process - as I say, this is not an area of interest of mine, so I am not full of detail...
I'm sorry I'm having a difficult time understanding. If it's not too much to ask, could you explain how you found the radius of the first circle a little more in depth?
Log in to reply
The link I gave to Pi Han has the details. We are trying to solve the simultaneous equations f 1 ( r , θ ) = ( 1 + r ) 2 ( 1 − 2 r 8 cos 8 θ + r 1 6 ) − ( 1 + r 8 ) 2 ( 1 − 2 r cos θ + r 2 ) f 2 ( r , θ ) = ( 1 + r ) 2 ( 1 − 2 r 9 cos 9 θ + r 1 8 ) − ( 1 + r 9 ) 2 ( 1 − 2 r cos θ + r 2 ) = 0 = 0 for r ≈ 0 . 9 3 , θ ≈ 0 . 7 3 (these values represent a reasonable guess). I square everything in these equations to make f 1 , f 2 differentiable. The two-dimensional Newton-Raphson iteration scheme makes us consider ( r n + 1 θ n + 1 ) = ( r n θ n ) − J ( r n , θ n ) − 1 ( f 1 ( r n , θ n ) f 2 ( r n , θ n ) ) where J is the Jacobi matrix J = ( ∂ r ∂ f 1 ∂ r ∂ f 2 ∂ θ ∂ f 1 ∂ θ ∂ f 2 ) While the 2D Newton-Raphson can be delicate, it works just fine in this case. If we choose ( θ 1 r 1 ) = ( 0 . 7 3 0 . 9 3 ) then I get the values for r and θ I mentioned in my proof, with 6 -digit accuracy, after four rounds of iteration.
For every largest circle added to the spiral, two more interstitial spaces are also added. See diagram. Let A be the area of the circle added, and B be the total area of the two interstitial spaces. Then R = A + B A as already explained.
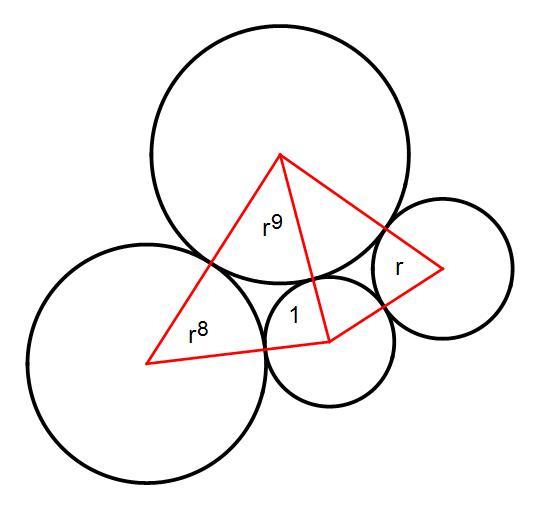
Finding the ratio r is another job. Given circle with radius 1 , it must be tangent to two tangent circles of radii r 8 , r 9 . Given vectors from origin to centers of circles of radii 1 , r , successive vectors must be in geometric progression. Solve. The ratio r works out to
r = 1 . 0 7 9 2 6 6 5 8 6 2 6 2 . . .
Let R be the distance from origin to circle of radius 1 . Then the distance from the origin to circle of radius r is R r . The triangle formed has sides R , 1 + r , R r . There are 2 unknowns r , R , and the tangency requirement with circles of radii r 8 , r 9 presents a system of 2 simultaneous equations to solve for those 2 unknowns. The solution is unique.
how come you get the r 8 , r 9 condition
Log in to reply
You count around the spiral until the first circle larger than 1 comes into contact with it, which is the 8th one. Then the 9th one touches it too, if the proportions are right. Remember, everything is in geometrical progression, it's a fractal.
You can pick any circle and say it has a radius of 1. Then start counting.
Log in to reply
I have explicitly added that condition into the statement.
Note: It is not apparent to me that the fractal nature must necessarily exist.
Log in to reply
@Calvin Lin – The problem asserts that such the fractal does exist. Then it's up to the reader to find the dimensions. If the solution is found, then the fractal indeed does exist, an unique one.
Finding the ratio r is another job. Given circle with radius 1 , it must be tangent to two tangent circles of radii r 8 , r 9 . Given vectors from origin to centers of circles of radii 1 , r , successive vectors must be in geometric progression. Solve. The ratio r works out to r = 1 . 0 7 9 2 6 6 5 8 6 2 6 2 . . .
Huh? What vectors are you speaking of? And why does your r differ from Mark Hennings' r ?
Log in to reply
Becuase they are using different notation. Notice that "Michael's r * Mark's r = 1".
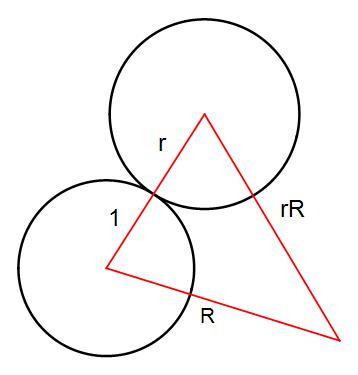
How did you know that the distance from the origin to the circle with radius r is Rr? I am a little confused?
Log in to reply
Check this figure below. Start with a unit circle at distance R from the origin.(0,0). Then the next larger circle which has a radius of r, tangent to the unit circle, should be at a distance rR from the origin (0,0) in order for this to be a fractal. Repeat.
Also sorry to bother you but is there somewhere I can read more about this type of problem.
Let the largest circle have centre given by the complex number 1 , and the next largest circle have centre given by the complex number z , where ∣ z ∣ < 1 . Then the radius of the first circle is ρ = 1 + ∣ z ∣ ∣ 1 − z ∣ . In general, the n th circle has centre z n and radius ρ ∣ z ∣ n .
The fractal nature of the pattern is obtained provided that the 0 th, 8 th and 9 th circles are mutually tangent, which means that we require ∣ 1 − z 8 ∣ = ρ ( 1 + ∣ z ∣ 8 ) ∣ 1 − z 9 ∣ = ρ ( 1 + ∣ z ∣ 9 ) Solving these equations numerically, the only physically reasonable solution (for z with positive argument) occurs when z = r e i θ with r = 0 . 9 2 6 5 5 5 and θ = 0 . 7 3 1 6 0 2 .
Given the fractal nature of the diagram, the ratio R is the ratio A A + B B A A where A A is the area of the 0 th circle, namely A A = π ρ 2 = 0 . 4 0 5 9 4 , and B B is the sum of the interstitial area between the 0 th, 1 st and 9 th circles and the interstitial area between the 0 th, 8 th and 9 th circles. Since the radii of the circles are all known, this is an elementary calculation, and B B = 0 . 0 1 1 7 5 6 9 + 0 . 0 0 8 2 3 3 0 5 = 0 . 0 1 9 9 9 . Hence R = 0 . 9 5 3 0 6 7 , making the answer 9 5 3 .
Presumably, a similar fractal pattern could be generated with a number other than 8 circles required before the pattern reconnects...