Virus and mesh connected computers

Probability Level 2

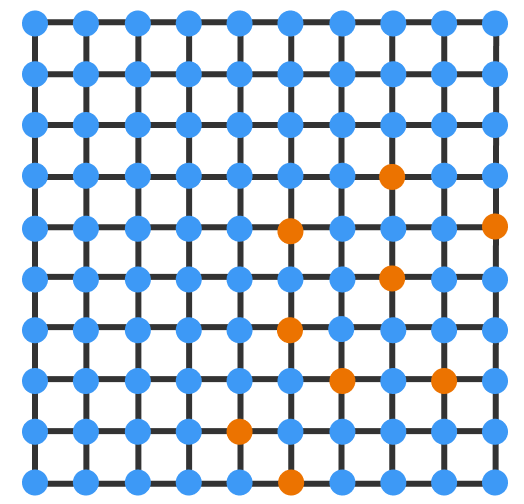
A mesh connected network consisting of $10 \times 10$ computers are arranged as shown. At the start, exactly 9 of these computers are infected with a virus. If any computer is directly connected to at least 2 infected neighbors, it will also become infected.

Will the virus infect all 100 computers (You must consider all $^{100}C_9$ initial cases)?

Note: This initial starting position shown below is provided as a single example.

Yes, always Yes, with a suitable starting position No, never

3 solutions

Wen Z
Dec 11, 2016

Consider the total perimeter of all viruses. It is at most 36 at the start and is non-increasing (can you see why?).

If all computers were infected at the end, then the perimeter is 40. Thus, there is no way that can happen.

Good use of the invariant principle .

Note that the total perimeter of all the viruses is at most 36 at the start. (It could be 12).

Calvin Lin Staff - 4 years, 6 months ago

How about we put the initial viruses diagonally? I think it will infect all the computers

Resha Dwika Hefni Al-Fahsi - 4 years, 4 months ago

Yes, that would work. It requires 10 cells on the diagonal.

Calvin Lin Staff - 4 years, 4 months ago

I understand now, ok tks

Resha Dwika Hefni Al-Fahsi - 4 years, 4 months ago

I like this puzzle! However in your solution I wish you would have more clearly defined what you mean by "perimeter." In the case of interior nodes it seems to be a count of edges from infected nodes to uninfected ones that are not contained within a closed path of edges between infected nodes, whereas in the case of the fully infected grid (perimeter = 40) it seems to be a count of edges between infected nodes? Or maybe we can define perimeter always in the former way and consider the 10x10 grid as part of a larger network.

Mark C - 4 years, 3 months ago

Saya Suka
Dec 8, 2016

It can spread at most to 9*9=81 points as the viruses outermost possible positions without breaking their contact with the group are to spread at 9 wide and 9 long. Because if a virus stand alone (no neighbours at the diamond around it), it cannot infect other healthy computers.

I think this solution assumes that we start with the initial setup in the picture. But, I believe that @Ossama Ismail intended the question to pertain to all possible setups. So, I think the solution needs to be generalized.

Geoff Pilling - 4 years, 6 months ago

Yes, I understand. I'm just asking for the generalisation because there exists a very nice solution.

Wen Z - 4 years, 6 months ago

A much more interesting question: is it possible if the viruses (9 of them) are arbitrarily placed at the start?

Wen Z - 4 years, 6 months ago

Yes, and it still won't take, because the worst it could get is 81% infection rate.

Saya Suka - 4 years, 6 months ago

Can you prove this?

Wen Z - 4 years, 6 months ago

Yeah, this can be done with a starting position of (1,1), (2,2), (3,3), (4,4), (5,5), (6,6), (7,7), (8,8), and (9,9)... Too bad we didn't have just one more! ;0)

Geoff Pilling - 4 years, 6 months ago

@Geoff Pilling – A really hard question that somebody once posed to me was how many ways can it be done if we had 10 viruses instead?

Wen Z - 4 years, 6 months ago

How about we put the initial viruses diagonally? I think it will infect all the computers

Resha Dwika Hefni Al-Fahsi - 4 years, 4 months ago

Zidane Zizo
Feb 3, 2017

I think that (10) is the minimum initial infected computers that's sufficient to initiate a chain reaction that will cause all computers to be infected in the end , and these ten units should be in the diagonal positions which will add another parallel infected line for each iteration till infecting all computers.

Indeed. The goal of this problem is to explain why 9 (or fewer) isn't sufficient. Of course, one way is to check all ${ 100 \choose 9 }$ possibilities to verify that 9 isn't sufficient. See the other solutions for another approach.

Calvin Lin Staff - 4 years, 4 months ago

Virus and mesh connected computers

3 solutions

0 pending reports