Visible cubes
Consider a 6 × 6 × 6 cube made up of 2 1 6 small cubes.
How many of these small 1 × 1 × 1 cubes are visible by rotating the larger cube?
The answer is 152.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
17 solutions
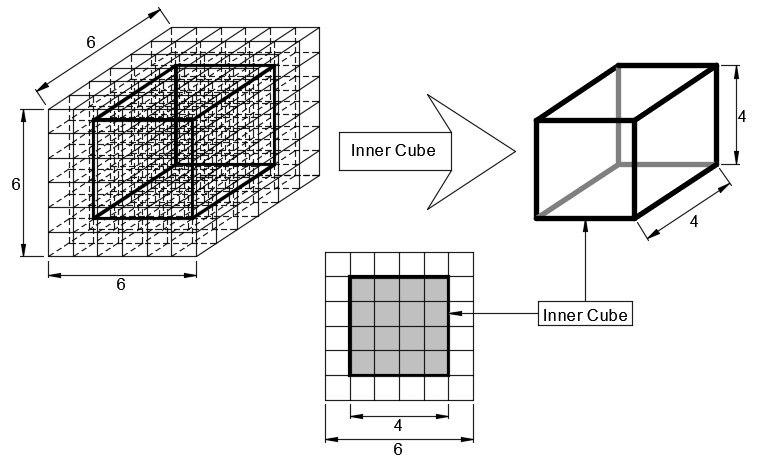 The outer shell (composed of unit cubes) is equal to the the volume of a 6x6x6 cube minus a 4x4x4 cube:
6
3
−
4
3
=
2
1
6
−
6
4
=
1
5
2
The outer shell (composed of unit cubes) is equal to the the volume of a 6x6x6 cube minus a 4x4x4 cube:
6
3
−
4
3
=
2
1
6
−
6
4
=
1
5
2
visible means what you can see in the image present!!!!!!!
Log in to reply
"visible by rotating" means from every single angle, not just what you can see in the image present
Log in to reply
No, it does not. It should have stated "rotating completely around in every direction."
Log in to reply
@Linda Slovik – it is just common sense ...
Log in to reply
@A Former Brilliant Member – What is "it?" You did not state what this thing is that you claim is common sense, nor who you are agreeing with or disagreeing with. Your post is vague/ambiguous, just as the directions for the problem are.
I believe it means from any angle, not just the image shown
My problem with this maths puzzle is in the wording and presentation. It's misleading that it provides you with an image of the 6x6x6 cube and concurrently asks you to answer how many individual cubes are visible. The puzzle adds: "(i.e. lie on the surface of the big cube ?)". It should state: "(i.e. lie on the surface of the big cube so that all sides were visible to the observer ?)". The image of the cube shows only three faces. I found myself trying to solve for the visible faces on the cube represented in the image, for only 3 faces. Communication is important, isn't it? Was it obvious to you, the community, that you knew what the author of this puzzle meant?
Log in to reply
I actually found it fairly obvious and never even considered that option. Wouldn’t be much of a puzzle to count the visible squares on the image.
Log in to reply
It says "by rotating the larger cube"... which is the same as saying "visible on all sides"...
Log in to reply
@John Roush – @ John Roush - Wrong. The phrase "by rotating the larger cube" is ambiguous. It is NOT the same as stating "visible on all sides," because it does not state "by rotating the larger cube all the way around and in every direction."
@ Alexander Nissen - Wrong. It would still be "much of a puzzle." It would also check knowledge of not overcounting.
Log in to reply
@Linda Slovik – I think when you wrote "Wrong" (to both of us) you really meant: "that isn't my opinion". In my opinion, it would be a very easy puzzle if you just needed to count the visible cubes - and I think very few would overcount on such a simple question. But it seems we will have to agree to disagree :)
I agree with Rupert. At no point, it is visible to YOU all sides of the cube. Now, if you say how many cubes are on the surface of the big cube than it is completely different. Math is precise discipline. Wording should be too.
I agree. I first did this. Then I did the whole cube.
Mathematics A regular solid having six congruent square faces. The correct answer with that definition is 180 if your point of view is static and the large cube is rotated.
why is the final cube having the volume of 4 and not 5 coz each box is of unit volume????Pls help.
Log in to reply
The dimensions of the inner cube are 4 because we need to subtract a cube from both sides.
How did you realize that you needed to subtract it by 4^3? What keyword told you or did you assume?
Log in to reply
Instead of looking at the cubes on the surface, he looked at the cubes on the inside. As the diagram shows, there is a 4x4x4 cube on the inside, so he must subtract 4^3 to get the answer.
Why couldn’t it be its surface area?
Log in to reply
Coz a cube is a 3D figure so when u rotate the larger cube it's not only the surface area that we are changing but also the depth.
That doesn't make any sense. The surface area of the cube is 6x6, meaning there are 36 cubes visible on each surface. since you can rotate the cube to see all 6 surfaces, you can count 36 cubes on each of the 6 surfaces of the cube. You can count this out... Why aren't the numbers lining up?
Log in to reply
This means that you are overcounting the number of cubes. Specifically, you are counting each edge cube twice, and each corner cube thrice.
I did this much longer, but hey, I got it right. Basically it's me thinking it out and correcting my mistakes
The invisible cubes form a cube of dimensions 4 × 4 × 4 . Thus the number of visible cubes is 6 3 − 4 3 = ( 6 − 4 ) ( 6 2 + 6 ⋅ 4 + 4 2 ) = 2 ⋅ 7 6 = 1 5 2 .
Bullshit! It says, VISIBLE.!
Log in to reply
It says: ... are visible (i.e. lie on the surface of the big cube) .
To calculate this, I took the total number of cubes and subtracted the number of invisible cubes.
Why should that be, as you so eloquently express, "bullshit"?
Exactly the same way I solved it. For the moaners, the key phrase in the question is 'by rotating the larger cube', which means that you will ultimately see all sux surfaces of the cube, hence why it is only the entirely internal (genuinely concealed) cubes that have to be deducted from the total.
General Case: Considering an n × n × n cube, we can see 6 n 2 − 1 2 n + 8 unit cubes.
First proof: Let w be the number of visible cubes. Using the already presented method of subtracting the "inner" cube, we have:
w = n 3 − ( n − 2 ) 3 = ( n − ( n − 2 ) ) ( n 2 + n ( n − 2 ) + ( n − 2 ) 2 ) = 2 ( 3 n 2 − 6 n + 4 ) (using the formula for the difference of two cubes), which is the desired result.
Second proof: There are 8 corner unit cubes, n − 2 edge unit cubes on each edge(there are 1 2 edges) and 6 inner faces containing ( n − 2 ) 2 cubes. Thus,
w = 6 ( n − 2 ) 2 + 8 + 1 2 ( n − 2 ) = 6 n 2 − 1 2 n + 8 .
For n n n cube, the number of unit cubes will be n^3/1 i.e. n^3. Why will it be a quadratic equation?
Log in to reply
...I don't get what you're referring to.
Perhaps the difference of cubes in the first proof has you confused...
Hear is Poca Poca 's first proof in simpler algebra.
First proof: Using the method of subtracting the "inner" cube.
Let w be the number of visible cubes.
Let n be the length of the cube.
The volume of the inner cube is
(
n
−
2
)
3
The Volume of the outer cube is
n
3
w
=
n
3
−
(
n
−
2
)
3
w
=
n
3
−
[
(
n
−
2
)
(
n
−
2
)
(
n
−
2
)
]
w
=
n
3
−
[
(
n
2
−
4
n
+
4
)
(
n
−
2
)
]
w
=
n
3
−
[
n
3
−
4
n
2
+
4
n
−
2
n
2
+
8
n
−
8
]
w
=
n
3
−
[
n
3
−
6
n
2
+
1
2
n
−
8
]
w
=
n
3
−
n
3
+
6
n
2
−
1
2
n
+
8
w
=
6
n
2
−
1
2
n
+
8
The cubes cancel each other out other than the surface layer.
It's asking for the number of visible unit cubes.
If your question
Why will it be a quadratic equation?
is an emotional ‘this doesn’t make intuitive sense’, then your intuition needs tuning. The goal is to find a figure for the amount of objects on the surface—without computing anything, one immediately expects a quadratic (‘2-dimensional’) expression.
I kinda thought a cube has 6 faces with n^2 squares/cubes. I deduct the 12 edges cubes (6 each edge) cause they are counted twice and the 8 corner cubes twice more cause they are counted two more extra time. So 6 n^2-12 (n-2)-8 2 = 6 6^2-12 4-16 = 216 -48 -16 = 152 It is the same 6n^2 - 12n + 8 equationI kinda thought a cube has 6 faces with n^2 squares/cubes. I deduct the 12 edges cubes (6 each edge) cause they are counted twice and the 8 corner cubes twice more cause they are counted two more extra time. So 6 n^2-12 (n-2)-8x2 = 6 6^2-12x4-16 = 216 -48 -16 = 152 It is the same 6n^2 - 12n + 8 equation
Dear Polka, You like burn up pencil lead ...!
Why not just leave it at n 3 − ( n − 2 ) 3 ? Also if you want to (for whatever reason) ‘expand’ the term, then use alternating polynomials: n 3 − ( n − 2 ) 3 = ( n − 1 + 1 ) 3 − ( n − 1 − 1 ) 3 = 6 ( n − 1 ) 2 + 2 which is a lot faster.
All the small 1 ∗ 1 ∗ 1 cubes on the faces, edges, or vertices of the big cube are visible. There are 6 faces, 1 2 edges, and 8 vertices on a cube.
Each vertex of the big cube has 1 small cube on it. 8 vertices ∗ 1 cube per vertex = 8 .
Each edge of the big cube has 4 small cubes that are not already counted in the vertices. 1 2 edges ∗ 4 cube per vertex = 4 8 .
Each face of the big cube has 1 6 small cubes in it that are not already counted in the edges or vertices. 6 vertices ∗ 1 6 cube per vertex = 9 6 .
Add them all up: 8 for vertices + 4 8 for edges + 9 6 for faces = 1 5 2 total cubes.
The answer is
| 1 5 2 |
Splendid solution. You can also work it out by eliminating the completely invisible cubes, those that are inside the larger structure, which themselves form a 4 x 4 x 4 cube, giving you (6 ^ 3) - (4 ^ 3) = 216 - 64 = 152.
Log in to reply
oh thanks that's easier
There are 8 corners (sometimes also called "vertices") on the large cube. That's 8 small cubes
There are 12 edges to the cube. Each edge has 4 small cubes in the middle (we already counted the outer cubes of the edges as they are corners). So that's 4 × 1 2 = 4 8 small cubes.
Finally, each of the 6 faces of the cube has 16 small cubes that don't lie on any edge. That's a total of 6 × 1 6 = 9 6 small cubes to count for the faces.
So, the answer must be 8 + 4 8 + 9 6 = 1 5 2 small cubes being visible.
There are (6-2)^3=64 little cubes that are not visible (look at the inner 4×4×4 cube), so 216-64=152 little cubes are visible.
You can't just calculate 6 × 6 × 6 because that gives you the number of faces not cubes. The cubes in the corners show 3 faces, and the ones in the edges show 2. Those extra faces need to be subtracted to get the correct solution.
Instead of counting the number of unit cubes on the surface, count the number of unit cubes that are not on the surface. The inside of the large cube is another cube with dimensions 4 × 4 × 4 , so there are 6 4 unit cubes inside the large cube. There are 2 1 6 − 6 4 = 1 5 2 cubes which are on the outside of the large cube.
Side 1) 6 x 6= 36
Side 2) 5 x 6= 30
Sides 3+4) 2(5 x 5)= 50
Side 5) 4 x 5= 20
Side 6) 4 x 4= 16
Solution----- 36+30+50+20+16 = 152
2 whole faces: 6 × 6 × 2 = 7 2
2 partial faces, with the opposite end rows being accounted for: 4 × 6 × 2 = 4 8
2 partial faces with all 4 sides being accounted for: 4 × 4 × 2 = 3 2
7 2 + 4 8 + 3 2 = 1 5 2
I didn't use the "inner cube method" (good method though: really fast!) because I didn't think about it; so I thought my solution could be useful to people who may want an alternative to that method. Consider one of the six surfaces of the cube - call it A. If you draw it (and please divide it into the 6x6 squares it is made of), you can see that: - There are 4 cubes (at the vertices) that this surface has in common with two other surfaces; - There are 1 6 cubes (at the corners) that this surface has in common with another surface; - There are 1 6 cubes (in the middle) that this surface has only on itself.
| Number of cubes in A | Surfaces that have these cubes in common |
| 4 | 3 |
| 16 | 2 |
| 16 | 1 |
And this happens for all the surfaces: at every vertice we have three surfaces that bump into each other and at every corner we have two of them. To count the total, we can simply add up all the cubes; but pay attention: this isn't simply multiplying every row of the table above by six. For example, think about the four cubes that appear on three surfaces. That means that if we count them on surface A and then consider surface B, which is consecutive to A, we don't need to count them again, because they are literally the same cubes; and this is the same for another surface, call it C, consecutive to A and to B. To be more general, if a cube is in common with N surfaces, we have to multiply it for N 6 to get the total. So, for each row of the table above, we have:
| Number of cubes in A | Multiplied by... | To get |
| 4 | 2 | 8 |
| 16 | 3 | 48 |
| 16 | 6 | 96 |
Add up the numbers in the last column to get the total: 8 + 4 8 + 9 6 = 1 5 2 .
I counted :) I counted the number of columns (6 6 would have repeated the corners): 20, multiplied 6 20, then accounted for the 16 squares visible on the top and the bottom. (16*2) + 120 = 152
Next level inner cube is 4x4x4. Subtract this sum from 6x6x6. 216 minus 64 is 152.
Outer cube - inner cube => (6x6x6)-(4x4x4)=216-64=152
露出3个面:8(8个角);露出2个面: 1 2 × 4 = 4 8 (12条边);露出一个面: 6 × 4 2 = 9 6 (6个面)。共计8+48+96=152个。
Number of outer cubes = 4 n ( n − 1 ) + 2 ( n − 2 ) 2 = 4 × 1 0 × ( 1 0 − 1 ) + 2 × ( 1 0 − 2 ) 2 = 4 0 × 9 + 2 × 6 4 = 3 6 0 + 1 2 8 = 4 8 8