Trigonometry! #2
If sec θ − tan θ = p 1 , then csc θ is equal to:
This problem is part of the set Trigonometry .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Well I was dumb and clicked the wrong button, but here's my alternative solution using pure Geometry since I hate trig. Lol
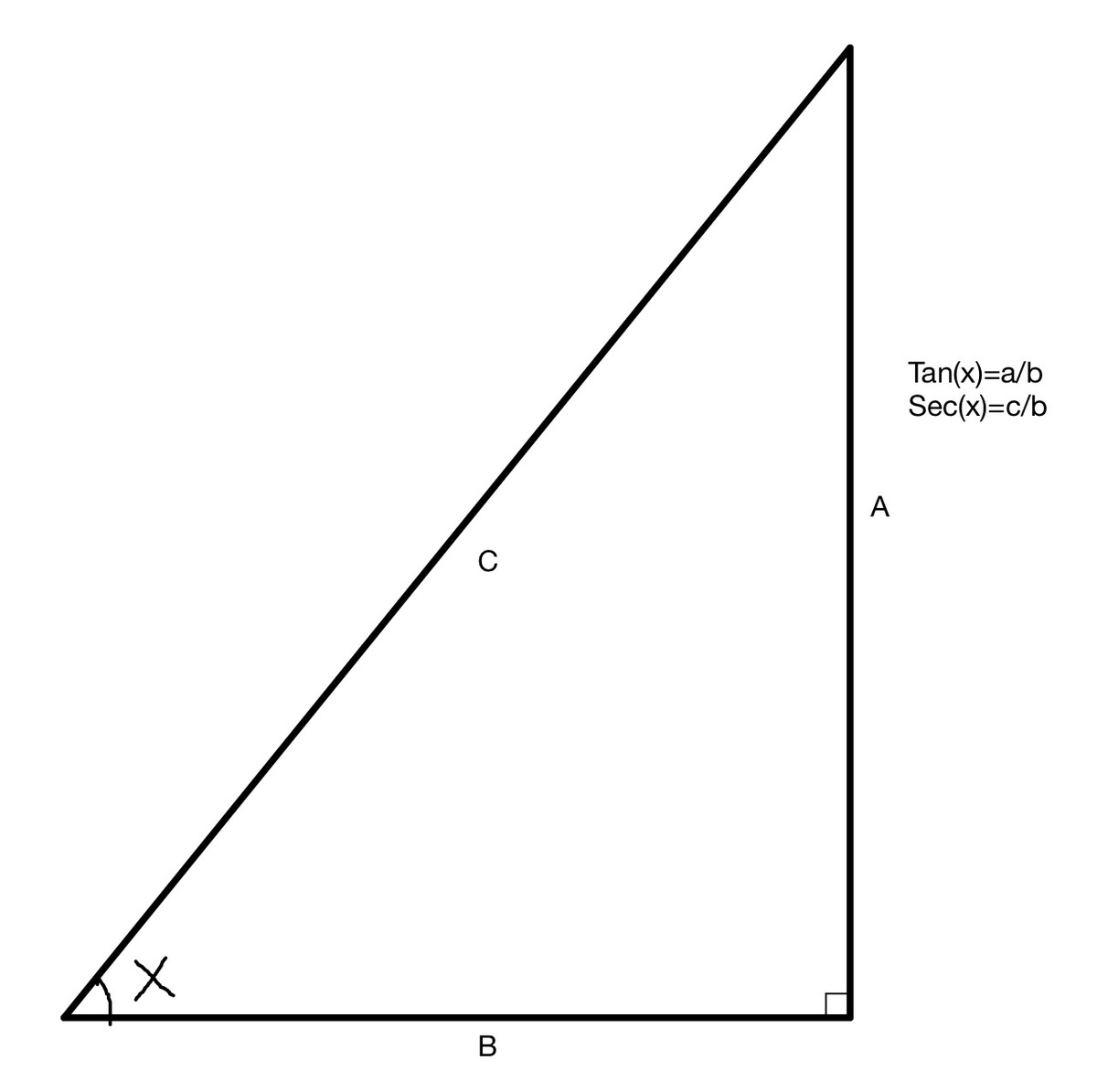
sec ( x ) = b c , tan ( x ) = b a
sec ( x ) − tan ( x ) = b c − b a = b c − a = p 1
Using some logic and the ever useful powers of laziness, we let a = c − 1 and b = p
b c − a ⇒ p c − ( c − 1 ) = p 1
Using Pythagorean theorem
c 2 = a 2 + b 2 ⇒ ( c − 1 ) 2 + p 2
c 2 = c 2 − 2 c + 1 + p 2
2 c − 1 = p 2
c = 2 p 2 + 1
Since earlier we let a = c − 1 we substitute for c to get
a = ( 2 p 2 + 1 ) − 1 = 2 p 2 − 1
Now, csc x = a c , substituting our values for c and a in terms of p we get
csc x = a c ⇒ 2 p 2 − 1 2 p 2 + 1 = p 2 − 1 p 2 + 1
I don't see any significance in taking θ = x though. :\
Log in to reply
Because we're just too lazy to type \theta. :P
Good solution ...I did same but the I selected the option of sin (theta) instead of cosec(theta) by mistake......:-)
Log in to reply
Wow same mistake pressed wrong!
Log in to reply
Lol, so many people clicking the wrong choice I edited in "CHOOSE CAREFULLY"
Log in to reply
@Trevor Arashiro – I clicked the wrong choice, probably after reading "Choose Carefully" -_-
Log in to reply
@Satvik Golechha – XD, "Why do smart people do dumb things"
Answer, "because they read the directions carefully"
Log in to reply
@Trevor Arashiro – And what about dumb people sometimes doing smart things? :-P
Log in to reply
@Satvik Golechha – Durphy's Law: When Murphy's law can go wrong, it will.
I pressed the answer you have solved but it showed that I was wrong . Do something about it !!!!
Log in to reply
I have wrote the answer of sinx , we have to press for cscx , same mistake you and others did
A very elegant solution!!
θ = x
( s e c x − t a n x ) ( s e c x + t a n x ) = 1
2 s e c x = p + p 1
c o s x = 1 + p 2 2 p
s i n x = 1 − c o s 2 x = ( 1 + p ) 2 1 + p 4 − 2 p 2 = p 2 + 1 p 2 − 1